Лекция 12 Резервирование с дробной кратностью
При резервировании с дробной кратностью система может функционировать, если из «n» однотипных работающих параллельно элементов в работоспособном состоянии находятся «r» элементов. Система отказывает, если число отказавших элементов «z» составляет:
.
Используя метод перебора состояний, найдем вероятность отказа такой системы
Q = P{z=m}+P{z=m+1}+…+P{z=n}
В
каждом из состояний число работоспособных
элементов составляет n-z,
а вероятность этого состояния
тогда
где
-
число сочетаний из n
элементов по z
при q«1
Без резерва система включает «r» работающих элементов. Поэтому вероятность отказа исходной системы составляет:
.
Так,
если система включает три параллельно
работающих элемента (n=3),
r
=2, q=0,1,
то
m=n-r+1=3-2+1=2.
Тогда для резервной системы:
.
Тогда
показатель снижения вероятности отказа
(выигрыш резервирования) определяется
выражением
.
Поэлементное резервирование
Надежность системы, содержащей группы элементов или отдельные элементы с поэлементным резервированием рассчитываются с помощью формул общего постоянного резервирования.
Так,
если система состоит из «n»
участков с поэлементным резервированием
целой кратности
,
то вероятность
безотказной работы системы:
,
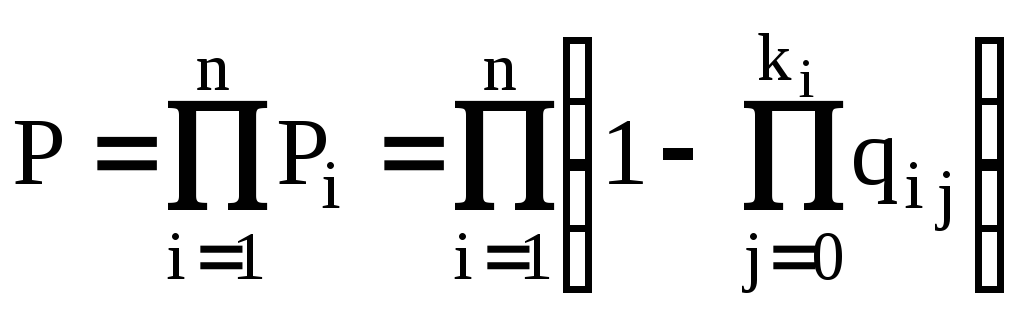где
вероятность отказа j–го
элемента, входящего в i-й
участок резервирования.
Рассмотрим
две системы содержащих одинаковое число
«
»
равнонадежных элементов:
|
…
Ø … Ø … |
…
Ø … … Ø |
Для первой схемы осуществляется общее резервирование системы из «n» элементов кратностью «k».
Для второй схемы при поэлементном резервировании каждый из «n» элементов системы имеет k резервных.
В
первом случае
вероятность отказа системы с
общим резервированием
определяется выражением
.
Считая,
что вероятность отказа каждого из
элементов
,
получим:
;
.
Для
второго случая вероятность отказа
системы с
поэлементным резервированием
.
Эффективность поэлементного резервирования составит
.
Таким образом, с увеличением глубины «n» и кратности резервирования «k» эффективность резервирования увеличивается.
Однако использование поэлементного резервирования сопряжено с введением дополнительных подключающих элементов, имеющих ограниченную надежность.
Поэтому
существует оптимальная
глубина резервирования
.
При
эффективность резервирования уменьшается.
Лекция 13 Резервирование двухполюсных элементов
В большинстве случаев резервные элементы подключают параллельно основному. Резервирование по видам отказов может осуществляться при различных способах включения резервных элементов. Двухполюсные релейные элементы (герконы, реле, пускатели и т.п.) включаются в электрическую цепь последовательно, либо параллельно. Поэтому в дальнейшем рассматривается эффективность резервирования двухполюсных элементов при последовательном и параллельном их включении.
Наиболее характерным является резервирование релейных элементов при отказах типа «обрыв» и «короткое замыкание».
Двухполюсные элементы релейного типа, имеют два возможных состояния:
1 – несрабатывание при наличии управляющего сигнала;
2– ложное срабатывание при отсутствии управляющего сигнала.