Добавил:

amodron Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ms_labs

.pdf

Скачиваний:

Добавлен:

10.12.2018

Размер:

4.28 Mб

Скачать

☆

1 / 171 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

ЛАБОРАТОРНА РОБОТА № 1

ВИКОРИСТАННЯ ЛОГІЧНИХ ОПЕРАТОРІВ В ЕXCEL

Мета роботи: Ознайомитись з методикою та набути початкових навичок використання логічних функцій для організації розрахунків в табличному процесорі Excel.

1. Загальні положення.

Логічні функції використовують для організації обчислень в тому випадку, коли необхідно виконувати ті чи інші дії залежно від виконання деяких умов. Excel дозволяє використовувати наступні логічні функції:

Таблиця 1

Логічні оператори

Логічні оператори прийнятими			Виконувані функції
	мовами

українськ	англійськ	російська
а	а

ЯКЩО ( )	IF ( )	ЕСЛИ ( )	Приймає те чи інше значення в
			залежності від виконання умови

І ( )	AND ( )	И ( )	Приймає значення ІСТИНА, якщо
			значення ІСТИНА приймають усі
			аргументи

АБО ( )	OR ( )	ИЛИ ( )	Приймає значення ІСТИНА, якщо
			хоча б один аргумент приймає
			значення ІСТИНА

НЕ ( )	NOT ( )	НЕ ( )	Змінює значення свого аргументу на
			протилежне

Для перевірки істинності умови використовують логічні вирази – вирази, утворені математичними операторами, функціями та аргументами, серед яких обов’язково є хоча б один логічний оператор. Результатом логічного виразу є логічні значення ІСТИНА ( "1" ) або ХИБНІСТЬ ( "0" ).

2.Реалізація логічних функцій.

2.1.Функція І ( ). Логічне множення: повертає значення ІСТИНА, якщо всі аргументи мають значення ІСТИНА; повертає значення ХИБНІСТЬ,

якщо хоча б один аргумент має значення ХИБНІСТЬ. Записується в такий спосіб:

І(логічне_значення1; логічне_значення2; …)

Тобто, функція приймає логічне значення ІСТИНА, лише якщо всі аргументи є істиною. Функція може мати від одного до тридцяти аргументів. Аргументи повинні бути або логічними значеннями, або масивами, або посиланнями на комірки, в яких містяться логічні значення.

Приклади:

1.І(ІСТИНА;ІСТИНА)=ІСТИНА.

2.І(ХИБА;ІСТИНА)=ХИБА.

3.І(2+2=4;2+3=5)=ІСТИНА (обидва аргументи функції є логічними виразами, які завжди приймають значення ІСТИНА).

4.І(A3;C7) – значення яке прийме функція, залежить від значень, що містяться в комірках A3 та C7; якщо в комірках A3 та C7 знаходяться логічні значення ІСТИНА, то функція приймає значення ІСТИНА. В усіх інших випадках функція прийматиме значення ХИБА.

5.І(В1:В3) – значення, яке прийме функція, залежить від значень, що містяться в діапазоні комірок В1:В3. якщо в комірках В1:В3 містяться значення ІСТИНА, ХИБА і ІСТИНА то І(В1:В3)=ХИБА.

2.2.Функція АБО ( ). Функція приймає логічне значення ІСТИНА, якщо хоча б один її аргумент має логічне значення ІСТИНА і приймає значення ХИБА, якщо усі її аргументи приймають значення ХИБА. Цю функцію записують так:

АБО(логічне_значення1; логічне_значення2; …)

Функція може мати від 1 до 30 аргументів. Аргументи повинні бути або логічними значеннями, або масивами, або посиланнями на комірки, в яких містяться логічні значення.

Приклади:

1.АБО(ІСТИНА;ХИБА)=ІСТИНА.

2.АБО(ХИБА;ХИБА)=ХИБА.

3.АБО(2+2=4;2+3=5)=ІСТИНА (обидва аргументи функції є логічними виразами, які завжди приймають значення ІСТИНА).

4.АБО(2+2=5;2+3=1)=ХИБА (обидва аргументи функції є логічними виразами, які завжди приймають значення ХИБА).

5.АБО(A3;C7) – значення яке прийме функція, залежить від значень, що містяться в комірках A3 та C7; якщо в комірках A3 та C7 знаходяться логічні значення ХИБА, то функція приймає значення ХИБА. В усіх інших випадках функція прийматиме значення ІСТИНА.

6.АБО(В1:В3) – значення, яке прийме функція, залежить від значень, що містяться в діапазоні комірок В1:В3. якщо в комірках В1:В3 містяться значення ІСТИНА, ХИБА і ІСТИНА то І(В1:В3)=ІСТИНА.

2.3. Функція ЯКЩО ( ). Записується в такий спосіб:

ЯКЩО(логічна умова, яку перевіряють; значення1; значення2)

Даний вираз можна розширити, тобто він допускає розгалуження за рахунок вкладання функцій

ЯКЩО(логічна умова, яку перевіряють; значення якщо істина; ЯКЩО(логічна умова, яку перевіряють; значення якщо істина; ЯКЩО(логічна умова, яку перевіряють; значення якщо істина; значення якщо хибність)

Приклад.

Табулювати функцію і побудувати її графік:

1 ln 1 x ,				x 0.2;
	1 x	0.5		x 0.2;
		0.5
				x 0.2, 0.8 ;
y			,
y	1 x		,
	1 x			x 0.8.
	2e 2x ,
	2e 2x ,

на проміжку 0,1				з кроком 0.1.

Розв’язок

1.Визначаємо діапазон зміни значень аргументу x та конкретні значення цього діапазону, використовуючи для цього процедуру автозаповнення з заданим кроком, наприклад, починаючи з комірки В6.

2.Поруч (справа) в сусідню комірку з коміркою першого значення аргументу x , тобто С6 вводимо формулу:

=ЕСЛИ(В6<0,2; 1+LN(1+B6); ЕСЛИ(И(В6>=0,2; B6<=0,8); (1+B6^(0.5))/(1+B6); 2*EXP(-2*B6)))

3.Використовуючи автозаповнення табулюємо функцію y .

ЗАВДАННЯ для самостійного розв’язування

Варіант № 1.

x 2; 2 і кроку 0.2 в

1. Побудувати графіки наступних функцій для

різних системах координат

y sin x e 2x ,

x 1,

1 x x

x 0,

1 cos

1 x

z 2ln 1

, x 1, 0 ,

2 x

sin2

x 0

1 x 3 5 ,

2 x

x 0.

2.Побудуйте в одній системі координат при x 2; 2 з кроком 0.1 графіки функцій: y 2sin x cos x , z 3cos2 2x sin x .

3.Побудуйте поверхню z x2 2 y2 при x, y 1; 1 (крок 0.1)

Варіант № 2.

1. Побудувати графіки наступних функцій для x 2; 2 і кроку 0.2:

	1 x	2						2	x ,	x 0,
	1 x				3sin x cos				x ,	x 0,
y				,	g					x 0.
y			2	,	g		2
	1 2x		2			3 1 x	2
	1 2x					3 1 x

		1 x		,	x 0;
					x 0;

	3 1 x2


					x 0,1 ;
z x 2e 2x ,					x 0,1 ;
		2 x	1 3	,	x 1.
			1 3

2.Побудуйте в одній системі координат при x 1; 3 з кроком 0.2 графіки таких двох функцій: y 2sin x 3cos x , z cos2 2 x 2 sin x .

3.Побудуйте поверхню z 3x2 2 y2 sin y при x, y 1; 1 (крок 0.1).

Варіант № 3.

1. Побудувати графіки наступних функцій для x 3; 1 і кроку 0.2:

x 0;

3x 1 x2 ,

x 0;

2 sin x

1 x

x 0,1 ;

z 2cos x e 2x ,

x 0.

2 sin 3x ,

x 1.

1 x

2. Побудуйте в одній системі координат при x 1; 2 , крок 0.1 графіки

наступних

двох

функцій:

y 5sin x cos 3 x sin x

та

zcos 2 x 2 sin3 x .

3.Побудуйте поверхню z 5x2 cos 2 y 2 y2e y при x, y 1; 1 , крок 0.1.

Вариант № 4.

1. Побудувати графіки наступних функцій для x 5; 1 і кроку 0.2

1 cos x

1 e2x

3 sin2 2x

x 0;

2cos2 x ,

x 0,1 ;

1 cos2

x 0;

x 0.

2 sin 3x

1 3

x 1.

2 1 2x ,

2. Побудуйте в одній системі координат при x 1; 4 , крок 0.2 графіки наступних двох функцій: y 3sin 2 x cos x cos 2 3 x та

z2cos2 2 x 3sin 3 x .

3.Побудуйте поверхню

	2x2 e y ,			x y		0.5,
	2x2 e y ,			x y		0.5,


z	xe2x y,		0.5		x y		1,
	2ex yey	,		1	x y		.
	2ex yey	,		1	x y		.


при x, y 2; 1.4			, крок 0.2.

Вариант № 5.

1. Побудувати в різних системах координат для x 1.8; 1.8 з кроком 0.2 графіки наступних функцій:

y 4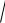1 e3x ;

1 / 3 ,

x 0,

3 sin x

x 0,

x 0,1 ,

1 x2

2x2

2x2 cos2 x ,

x 0;

x 1.

1 x

x 0; 3 , крок 0.1 графіки

Побудуйте в одній системі координат при

наступних двох функцій: y 2 sin x cos x та z cos2 x sin 3 x .

Побудуйте поверхню z 2x2 cos 2 x 2 y2

при x, y 1; 4 , крок 0.2.

Вариант № 6.

1. Побудуйте в різних системах координат для x 2; 1.8 з кроком 0.2 графіки наступних функцій:

y	2 3x	,

	1 x x2

											1 x			,			x 0,

										1 x			2
				2		2	x ,						2
	1 2x			2	sin	2		x 0,
													x
													x				x 0,1 ,
g			2 x					x 0;	z	1					,
g			2 x						z	1					,
							,			1		x

			e 0.1x
	3									sin 3x							x 1
		2							2	sin 3x						,	x 1

2.Побудуйте в одній системі координат при x 3; 0 , крок 0.2 графіки наступних двох функцій: y 3sin 3 x cos 2 x та z cos3 4 x sin x .

3.Побудуйте поверхню z 2e0.2x x2 2 y4 при x, y 2; 2 , крок 0.4.

Вариант № 7.

1. Побудуйте в різних системах координат для x 1,7; 1.6 з кроком 0.3 графіки наступних функцій:

1 x

2 x x2

1 x x

x 0,

1 x2

1 x

x 0,

x 0,1 ,

1 x

x 0;

1 x

1 e 0.2x

0.5 sin x

x 1.

2. Побудуйте в одній системі координат при x 3; 0 , крок 0.2 графіки

наступних

двох

функцій:

y 2 sin 2 x cos 4 x

та

zcos2 3 x cos x sin x .

3.Побудуйте поверхню z x2 2e0.2 y y2 при x, y 1; 1 , крок 0.2.

Вариант № 8.

1.Побудуйте в різних системах координат, коли x 1.5; 1.8 з кроком

0.2графіки таких функцій:

x3 / 5 3

x 3

x 0,

1.1 cos

x 0,

x sin

5.7

x 3,

1.2x

x 3,

x ,

1.2 5.7 e

x 3.

2. Побудуйте в одній системі координат при x 1; 2 , крок 0.2, графіки

двох

функцій:

y 2 sin 0.5 x sin 3.2 x

та

zcos2 1.5 x 3.4cos x sin 0.6 x .

3.Побудуйте поверхню z 2x2 3e0.4 y y0.5 при x, y 1; 1 , крок 0.1.

Вариант № 9.

1. Побудувати в різних системах координат при x 1.7;1.8 з кроком

0,3 графіки таких функцій:

1 xe x

x2 sin2 x

3 x

x 0,

x 0

1 3x

1 1 x 2 ,

x 0,1 ,

x 0

1 x

3 1 x

x 1.

1 cos2 x

2.Побудуйте в одній системі координат при x 0; 2 , крок 0.1, графіки двох функцій: y sin 3 x 2 sin 2 x cos 3 x та z cos x cos 3 x sin2 x .

3.Побудуйте поверхню

x e2 y ,

0.5,

2x2 e y ,

0.5

e2x y,

при x, y 1; 1 , крок 0.1.

Вариант № 10.

1. Побудувати в різних системах координат при

0.2 графіки таких функцій:

1 xe x

sin2

x ,

2 x2

1 2x

x 0,

1 x2 ,

z sin2 x

1 x ,

1 x

0.2x

, x 0.

sin x e

cos

x 1.4; 2.2 з кроком

x0,

x0,1 ,

x1.

2. Побудуйте в одній системі координат при x 0; 2 , крок 0.2, графіки двох функцій:

y cos 3 x 2 sin 3 x cos 2 x та z cos2 x cos 3 x .

3. Побудуйте поверхню

	2	3y		2	,	x	2	y	2	1,
x
z		2		3			2		2
			y		,	x		y		1.
3x

при x, y 1; 1 , крок 0.2.

Вариант № 11.

1. Побудувати в різних системах координат при x 1.4;1.4 з кроком 0.2 графіки наступних функцій.

1 x

e x

sin x

e 2x ,

x 0;

1 x2 ,

x 0,

1 x

1 x2

x 0,1 ;

, x 0,

sin

sin x

cos

3x,

x 1.

1 x

Вариант № 12.

1. Побудувати в різних системах координат графіки наступних функцій на проміжку 1; 10 з кроком 1.0 при a 17.3 , b 0.36 :

	esin
y	esin			4 a	,
y		ln3b			,
		ln3b
		2
	3sin x cos x ,
g 3
g 3			2
		1 x		,
		1 x		,

ln2

12 x

x 4,

5.7 x

x 0,

3 x ,

x 4,

x 0,

x 4,

1.2

5.7 x

Вариант № 13.

1. Побудуйте в різних системах координат на проміжку 2; 15 з кроком 1 при a 1.35 , b 8.4 графіки таких функцій:

1.7x

x 7,

6.2 x3

, x 1,

a b

1 x x2

z sin3 x2

x ,

x 7,

sin2

3 / 5

x 0,

6.2 e

x / 6

x 7.

1 x

Вариант № 14.

1. Побудуйте в різних системах координат на проміжку 1; 10 з кроком 1 при a 1.8 , b 0.56 графіки таких функцій:

tg2

e b

x 6,

1.7x

1 x

6x 1

x 0,

x 6,

ex ,

1 x3

1 / 3

x 1,

tg2

1.7x 4 e5 x ,

x 6.

Варіант № 15.

1.Побудуйте в різних системах координат на проміжку 1; 5 з кроком

0.5при a 0.3, b 9.5 графіки таких функцій:

x 0,

2 cos x e

2 sin 3x ,

x 0,

b 1.6

ln4 7.3x

x 4,

9.1 x

1.23

5 x ,

x 4,

17x

lg2 x 4

ln x ,

x 4.

5.2

x 0; 3 з кроком 0.2

2. Побудуйте в одній системі координат при

графіки

наступних

двох

функцій:

y 3cos x cos x sin 4x ,

z cos3 x sin 2 x .

1 / 171 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.12.20184.28 Mб25ms_labs.pdf
#
10.12.20184.58 Mб65ms_lec.pdf
#
10.12.20182.33 Mб37ms_prac.pdf
#
10.12.20181.78 Mб49Генетичні алгоритми.doc