Лекция №6 Расчет зубчатого зацепления на контактную прочность

Рис. 6.1

Расчет сводится к удовлетворению усло­вия, по которому контактные напряжения зубьев не должны превышать допускаемые. Расчет ведут для зацепления в полюсе (рис. 6.1), т.к. выкрашивание начинается у полюсной линии.

В качестве исходной принимают формулу Герца-Беляева для наибольших контактных напряжений при скольжении цилиндров, соприкасающихся вдоль образующей

. (6.1)

Входящие в формулу (6.1) величины известны из предыдущих лекций.

Обозначим - коэффициент, учитывающий механические свойства материала колес. Для стальных колес z_м=275 МПа.

Получим . (6.2)

Здесь - погонная нагрузка, где - длина контактных линий

(в прямозубых передачах );

Так как получаем . (6.3)

Приведенный радиус кривизны . По свойству эвольвенты

, поэтому и

Так как , следовательно

и . (6.4)

Подставив выражения (6.3) и (6.4) в уравнение (6.2), получим

.

Т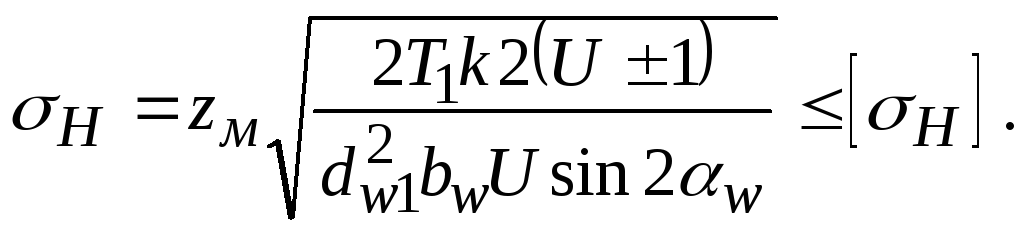 ак как , то

Обозначим - коэффициент, учитывающий форму сопряженных поверхностей ( при коэффициент), тогда

В передачах высокой точности (выше седьмой) вводится коэффициент , учитывающий влияние коэффициента торцевого перекрытия . Этот коэффициент получен экспериментальным путем. При отсутствии необходимости повышенной точности расчета можно принимать , что соответствует .

Окончательно получим

Таким образом, контактная прочность зубчатых колес определяется межосевым расстоянием, передаточным числом и шириной зубчатого венца, но не зависит от модуля.

Проектировочный расчет. Для проектировочного расчета представим ширину зубчатого венца в виде

(6.6)

где -коэффициент ширины зубчатого венца относительно межосевого расстояния .

Начальный диаметр шестерни выразим через передаточное отношение U и межосевое расстояние

(6.7)

Подставив выражения (6.6) и (6.7) в уравнение (6.5) и возведя обе части в квадрат, получим

о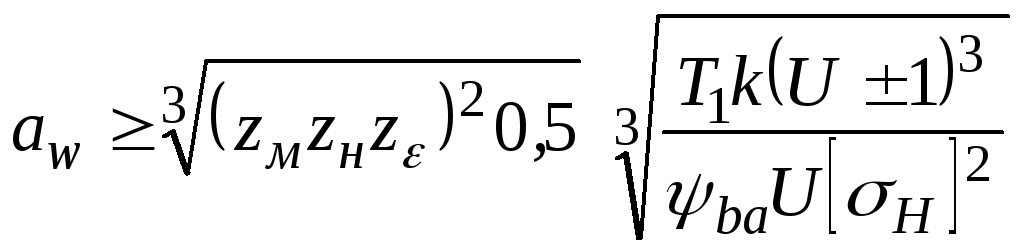 ткуда

или

,

где - вспомогательный коэффициент.

Для зубчатых передач низкой точности среднее значение этого коэффициента определяется по таблицам или графикам, приводимым в справочниках.

Расчет на изгибную прочность

Расчет зубьев на изгиб производится в предположении:

1. Вся нагрузка зацепления передается одной парой зубьев и приложена к вершине зуба, что возможно в том случае, если их деформации (разность основных шагов);

2. Зуб рассматривается как консольная балка, для которой справедливы методы сопротивления материалов;

3. Силами трения пренебрегаем.

Под нагрузкой зуб деформируется (рис 6.2), тогда угол .

Р

Рис. 6.2 Рис. 6.3

ассмотрим отдельно один зуб шестерни (рис.6.3).

Перенесём силу F_n вдоль линии зацепления, что возможно, ибо это окажет действие только на участке переноса, но никак не в опасном сечении по изгибу. Опасным будет сечение а-а' там, где балка равнопрочного сечения, имеющая вид параболы, пересекается с поверхностью зуба. Сила F_t' изгибает, а F_r' сжимает зуб. Согласно эпюре (рис. 6.3) напряжение в наиболее опасной точке a

. (6.8)

Изгибающие напряжения

,

где T_и – изгибающий момент;W– момент сопротивления изгибу в опасном сечении.

Размеры опасного сечения S₀ и b_w, а расстояние от точки приложения усилия до опасного расчетного сечения l₀.

Принимая и , получим

(6.9)

Напряжения сжатия определяются в виде

(6.10)

Подставив выражения (6.9) и (6.10) в равенство (6.8), с учетом концентрации напряжений у ножки зуба (учитывается коэффициентом k_ ), получим

, (6.11).

где ; (6.12)

(6.13)

В опасном сечение принимаем S₀=S’ и , где S’ и l’– безразмерные коэффициенты.

Подставив выражения (6.12) и (6.13) в уравнение (6.11), получим

Обозначим- коэффициент формы зуба. Это безразмерный коэффициент, величина которого зависит только от формы зуба (l’, S’, ’), в том числе и от формы галтели (k_). Ранее было показано, что форма зуба при одинаковом исходном контуре инструмента зависит в основном от числа зубьев колеса z и коэффициента смещения инструмента x,таким образом, Y_F=f(z, x, ).

Для колес с внутренним зацеплением

.

Условие прочности по изгибу будет

.

Учитывая, что , получим формулу для проверочного расчета

. (6.14)

Так как число зубьев шестерни и колеса различно, то различны Y_F1 и Y_F2, поэтому проверочный расчет для шестерни и колеса нужно делать отдельно.

Проектировочный расчет на изгиб. Возможны два варианта решения.

1. Рассмотрим случай, когда из расчета по контактным напряжениям известны a_w и b_w. Из формулы (6.14) выражаем , учитывая,

что , окончательно получаем выражение для модуля

.

2. Если габариты передачи определяются изгибной прочностью и известно z₁, то для некорригированной передачи d_w1=d₁=mz₁.

Обозначим , тогда

.

Откуда получаем выражение для определения модуля при проектировочном расчете

.