33)Поверхности второго порядка: эллипсойды, гиперболойды, парабалойды. Свойства.

O. Поверхностью второго порядка называется множество точек пространства, декартовы координаты которых удовлетворяют уравнению вида: F(x,y,z) = 0 или Ax²+By²+Cz²+Dxy+Exz+Fyz+Gx+Ly+Mz+N = 0 (*),

где A²+B²+C²+D²+E²+F²≠0.

O. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется эллипсоидом.

Свойства эллипсоида:

• Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что

• Эллипсоид обладает центральной симметрией относительно начала координат, осевой симметрией относительно координатных осей, плоскостной симметрией относительно начала координат.

• В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.

O. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, называется эллиптическим параболоидом.

Свойства эллиптического параболоида.

• Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

• Эллиптический параболоид обладает

осевой симметрией относительно оси Oz,

плоскостной симметрией относительно координатных осей Oxz и Oyz.

• В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.

O. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, называется гиперболическим параболоидом.

Свойства гиперболического параболоида.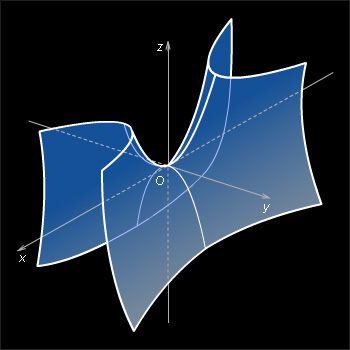

• Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

• Гиперболический параболоид обладает осевой симметрией относительно оси Oz, плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.

• В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается гипербола, а плоскостями, ортогональными осям Ox и Oy, – парабола.

• Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

O. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

a > 0, b > 0, c > 0, называется однополостным гиперболоидом.

Свойства однополостного гиперболоида.

• Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

• Однополостной гиперболоид обладает центральной симметрией относительно начала координат, осевой симметрией относительно всех координатных осей, плоскостной симметрией относительно всех координатных плоскостей.

• В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.

O. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.

Свойства двуполостного гиперболоида.

• Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что и неограничен сверху.

• Двуполостный гиперболоид обладает центральной симметрией относительно начала координат, осевой симметрией относительно всех координатных осей, плоскостной симметрией относительно всех координатных плоскостей.

• В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при получается эллипс, при – точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола.

По аналогии с коническими сечениями существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x2 = 0 описывается пара совпадающих плоскостей, уравнением x2 = 1 – пара параллельных плоскостей, уравнением x2 – y2 = 0 – пара пересекающихся плоскостей. Уравнение x2 + y2 + z2 = 0 описывает точку с координатами (0; 0; 0), уравнение x2 + y2 = 1 – круговой цилиндр, уравнение x2 + y2 = z2 – круговой конус. Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии.