20) Уравнение линии на плоскости. Уравнение прямой на плоскости, заданной точкой и направляющим вектором. Векторно-параметрическое и параметрическое уравнение прямой.

О. Уравнение F(х,у)=0, связывающее координаты х,у наз. уравнением линии L, если координаты х,у всякой точки линии L удовлетворяют этому уравнению, а координаты всякой точки, не лежащей на линии L, не удовлетворяюют уравнению.

Обозначение: L; l; AB

Можно координаты х,у выразить через произвольный параметр t, в виде уравнения:

Х=Х(t)

Y=Y(t) – такие уравнения наз. параметрическими уравнениями линии.

Прямая на плоскости может быть задана точкой M(0,0) и направляющим вектором ={q₁, q₂}:

Возьмем М(х,у)

Вектор М₀М={x-x₀; y-y₀}

Вектор М₀М коллинеарен вектору

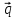
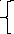
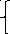Тогда по условии коллинеарности : М₀М= t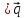

x - x₀­­ = tq_­1 x = x₀­­ + tq_­1

y – y_­0­ = tq_­2­ y = y_­0­ + tq_­2­ – параметрическое уравнение прямой (1) t

t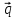 = 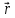– 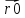- векторно-параметрическое уравнение прямой.

Есл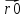и и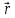 – радиус векторы точки М_{0 ­}и М,

Тогда =–

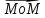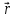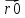
21) Каноническое уравнение прямой на плоскости. Уравнение прямой с угловым коэффициентом. Уравнение прямой, заданной двумя точками. Прямая в «отрезках».

Если q_­1 ­≠ 0 и q_­2 ≠ 0, то получим каноническое уравнение прямой : =

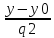
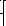Из системы x - x₀­­ = tq_­1

y – y_­0­ = tq_­2­ выразим t :

t = 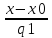, тогда у – у_­0­ =

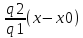
y = y_­0­ +

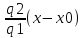
y = kx + y_­0­ – kx_­0

­y = kx + b – уравнение прямой с угловым коэффициентом k

Прямая задана двумя точками M_­1­(x_­1­; y_­1­); M_­2­_­­(x­_­2­; y_­2­) :

= {x_­2 – x₁­; y_­2­ – y_­1­} – направляющий вектор прямой

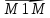= {x - x_­1; y – y_­1}

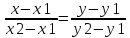– уравнение прямой проходящей через 2 точки

Пусть прямая проходит через А(a;0) и B(0;b)

-

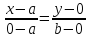
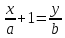
– уравнение прямой в отрезках

22) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение прямой, частные случаи.

M (x, y)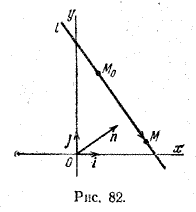

MoM = { x – x_­0­ , y – y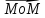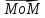_­0­ }

┴, * = 0

A(x – x_­0) + B(y – y_­0) = 0 - уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Ax + By – Ax_­0­ – By_{­0 ­} = 0

Ax + By ­ + C_­ = 0 - общее уравнение прямой

• С = 0, Ах + By = 0 – прямая проходит через начало координат

• А = 0, Ву + С = 0 – прямая параллельна ОХ

• В = 0, Ах + С = 0 - прямая параллельна ОУ

• А = 0 С = 0, Ву = 0, у = 0

23) Взаимное расположение прямых на плоскости. Угол между прямыми.

Тангенс угла между двумя прямыми вычисляется по формуле:

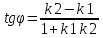
Необходимое и достаточное условие параллельности прямых, заданными уавнениями вида

y = k₁x + b₁ , y = k₂x + b₂ , выражается равенством k₁ = k₂, а условие их перпендикулярности – равенством:

k₁ = -

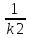
Если уравнения заданы уравнениями :

A₁x + B₁y ­ + C_­1 = 0 (1)

A₂x + B₂y ­ + C_­2 = 0, (2)

То тангенс угла определяется формулой:

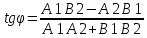
Необходимое и достаточное условие параллельности прямых, заданными уавнениями вида

(1), (2), выражается равенством k₁ = k₂, а условие их перпендикулярности – равенством:

, а условие их перпендикулярности:

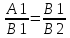- или A₁A₂ + B₁B₂ = 0 .