
- •20) Уравнение линии на плоскости. Уравнение прямой на плоскости, заданной точкой и направляющим вектором. Векторно-параметрическое и параметрическое уравнение прямой.
- •21) Каноническое уравнение прямой на плоскости. Уравнение прямой с угловым коэффициентом. Уравнение прямой, заданной двумя точками. Прямая в «отрезках».
- •22) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение прямой, частные случаи.
- •23) Взаимное расположение прямых на плоскости. Угол между прямыми.
- •24) Нормальное уравнение прямой на плоскости. Расстояние от точки до прямой.
- •25) Кривые второго порядка на плоскости. Эллипс: определение, вывод канонического уравнения, исследование формы, эксцентриситет, фокальные радиусы, дирекрисы, вершины.
- •26) Гипербола: определение, каноническое уравнение, асимптоты, эксцентриситет, директрисы, вершины.
- •27) Парабола: определение, вывод канонического уравнения. Расположение параболы в декартовой системе координат, координаты фокуса и уравнение директрисы. Частные случаи.
- •28) Плоскость в пространстве r3. Уравнения плоскости: по точке и нормальному вектору, общее уравнение плоскости, частные случаи.
- •29) Векторное уравнение плоскости. Уравнение плоскости, проходящей через три заданные точки. Плоскость в «отрезках». Нормальное уравнение плоскости.
- •30) Угол между двумя плоскостями. Взаимное положение плоскостей в пространстве. Расстояние от точки до плоскости.
- •31) Прямая в пространстве r3. Векторное уравнение прямой. Канонические и параметрические уравнения прямой. Уравнения прямой, проходящей через две точки. Общее уравнение прямой.
- •32) Взаимное расположение прямой и плоскости в пространстве r3. Угол между прямой и плоскостью. Условие принадлежности прямой плоскости.
- •33)Поверхности второго порядка: эллипсойды, гиперболойды, парабалойды. Свойства.
- •34) Поверхности второго порядка: конусы, цилиндры. Свойства.
- •35) Полярная система координат и ее связь с декартовой. Примеры кривых в полярной системе координат.
- •36) Цилиндрическая и сферическая системы координат и их связь с декартовой системой координат.
- •37) Высказывания и логические операции над ними. Предикаты, кванторы и связь между ними. Булева алгебра и ее приложения.
- •38) Алгебраические системы. Множества и операции над ними. Терминология и символика теории множеств.Числовые множества. Множества действительных чисел.Верхняя и нижняя границы множеств.
- •39) Множества комплексных чисел. Изображение комплексных чисел на плоскости. Алгебраическая форма записи комплексного числа. Операции над комплексными числами в алгебраической форме.
- •40) Тригонометрическая форма записи комплексного числа. Операции над комплексными числами в тригонометрической форме.
27) Парабола: определение, вывод канонического уравнения. Расположение параболы в декартовой системе координат, координаты фокуса и уравнение директрисы. Частные случаи.
О.
Параболой – называется
геометрическое место точек, равноудаленных
от данной точки F,
наз фокусом
и
данной прямой, наз директрисой.
ОС
= ОF
=

|MK|=|MF|
M(x;y)
K( )
)
|FM|=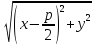
|KM|=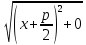
 =
=

y2 = 2px – каноническое уравнение параболы
Если р > 0, то ветви параболы направлены по направлению оси ОХ, если р < 0, то ветви направлены в противоположную сторону.
В
выбранной системе координат фокусом
параболы служит точка , а директриса
имеет уравнение ![]()
![]()
28) Плоскость в пространстве r3. Уравнения плоскости: по точке и нормальному вектору, общее уравнение плоскости, частные случаи.
О. Равенство F(x,y,z) = 0 или z = f(x,y) называется уравнением поверхности S, если координаты всех точек поверхности удовлетворяют этому уравнению, а координаты точек, непринадлежащих поверхности, ему неудовлетворяют.
Уравнения плоскости: точке и нормальному вектору:
M0
 M0
(x0,
y0,
z0)
M0
(x0,
y0,
z0)
 = {A,B,C} M (x, y, z)
= {A,B,C} M (x, y, z)

 ┴
┴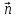 ,
значит
,
значит
 *
*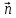 =
0
=
0
 A(x
– xo)
+ B(y – yo)
+ C(z – zo)
= 0 – уравнение
плоскости
A(x
– xo)
+ B(y – yo)
+ C(z – zo)
= 0 – уравнение
плоскости
Упростим уравнение: Ax + By + Cz – Axo – Byo – Czo = 0
Ax + By + Cz + D = 0 – общее уравнение плоскости
Частные случаи общего уравнения плоскости:
1) By + Cz + D = 0 - параллельна оси Ox;
2) Ax + Cz + D = 0 - параллельна оси Oy;
3) Ax + By + D = 0 - параллельна оси Oz;
4) Cz + D = 0 - параллельна оси Oxy;
5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz;
7) Ax + By + Cz = 0 - проходит через начало координат;
8) By + Cz = 0 - проходит через ось Ox;
9) Ax + Cz = 0 - проходит через ось Oy;
10) Ax + By = 0 - проходит через ось Oz;
11) z = 0 - плоскость Oxy;
12) y = 0 - плоскость Oxz;
13) x = 0 - плоскость Oyz.
29) Векторное уравнение плоскости. Уравнение плоскости, проходящей через три заданные точки. Плоскость в «отрезках». Нормальное уравнение плоскости.
Представим
вектор
 ,
через радиус веторы.
,
через радиус веторы.
 =
=

 =
=

( -
-
 ,
,
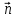 )
= 0
– векторное
уравнение, скалярное произведение
)
= 0
– векторное
уравнение, скалярное произведение
Уравнение плоскости, проходящей через М1(х1, y1, z1), М2(х2, y2, z2), М3(х3, y3, z3)
M1
M
 M
(x,
y, z)
M
(x,
y, z)
 = {x – x1,
y – y1,
z
– z1}
= {x – x1,
y – y1,
z
– z1}

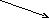
 = {x2
– x1,
y2
– y1,
z2
– z1}
= {x2
– x1,
y2
– y1,
z2
– z1}
 = {x3
– x1,
y3
– y1,
z3
– z1}
= {x3
– x1,
y3
– y1,
z3
– z1}
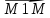 ,
,

 – компланарные
векторы.
– компланарные
векторы.
( ,
,

 )
= 0 –
смешанное
произведение
)
= 0 –
смешанное
произведение

 x – x1
y
– y1
z – z1
x – x1
y
– y1
z – z1
x2 – x1 y2 – y1 z2 – z1 = 0 - уравнение плоскости, проходящей через три точки
x3 – x1 y3 – y1 z3 – z1
Плоскость в «отрезках»
Пусть М1(a, 0, 0), М2(0, b, 0), М3(0, 0, c)
Тогда :

 x – a
y
z
x – a
y
z
– a b 0 = 0
– a 0 c
bc(x - a) + abz + acy = 0
bcx + acy + abz = abc | * (abc)
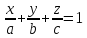 – уравнение плоскости в отрезках
– уравнение плоскости в отрезках
Нормальное уравнение плоскости.
Пусть плоскость задана : Ax + By + Cz + D = 0
A2
+ B2
+ C2
≠ 0
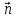 = {A, B, C}
= {A, B, C}
Введем
нормирующий
вектор :
Умножим уравнение плоскости на нормирующий вектор и получим:
cos x
+ cos
x
+ cos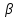 y
+cos
y
+cos z
– p = 0
- нормальное
уравнение плоскости
z
– p = 0
- нормальное
уравнение плоскости
P – расстояние от точки О(0,0,0) до плоскости
