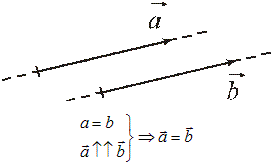Линейные операции над матрицами.

 

1.        Сложение матриц.

 

Определение 3.4. Суммой матриц А и В одинаковой размерности mn называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: 

                       Свойства сложения:

1.        А + В = В + А.

2.        (А + В) + С = А + (В + С) .

3.        Если О – нулевая матрица, то А + О = О + А = А

Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.

Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.

 

Пример.

   

 

2.        Умножение матрицы на число.

 

Определение 3.5. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

                          Свойства умножения матрицы на число:

1.        (km)A=k(mA).

2.        k(A + B) = kA + kB.

3.        (k + m)A = kA + mA.

 

Замечание 1. Справедливость свойств следует из определений 3.4 и 3.5.

 

Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е.        С = А + (-1)В.

 

Пример.

. Тогда  

 

                 Перемножение матриц.

 

Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго.

 

Определение 3.6. Произведением матрицы А размерности mp и матрицы В размерности  называется матрица С  размерности , каждый элемент которой  определяется формулой:  Таким образом, элемент  представляет собой сумму произведений элементов i-йcтроки матрицы А на соответствующие элементы j-го столбца матрицы В.

 

Пример.

. При этом существует произведение АВ, но не существует произведение ВА. Размерность матрицы С=АВ составляет  Найдем элементы матрицы С:  

Итак, 

 

Теорема 3.1 (без доказательства). Определитель произведения двух квадратных матриц равен произведению их определителей.

 

Замечание. Операция перемножения матриц некоммутативна, т.е.  Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей (см. предыдущий пример). Если существуют и АВ, и ВА, то они могут иметь разные размерности (если ).

    Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны.

Однако в некоторых случаях произведения АВ и ВА совпадают.

    Рассмотрим произведение квадратной матрицы А на единичную матрицу Е того же порядка:

Тот же результат получим и для произведения ЕА. Итак, для любой квадратной      матрицы А  АЕ = ЕА =А.

 

                        Обратная матрица.

 

Определение 3.7. Квадратная матрица А называется вырожденной, если , и невырожденной, если .

 

Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .

     Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.

 

Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы  исходная матрица была невырожденной.

 

Доказательство.

1)       Необходимость: так как  то  (теорема 3.1), поэтому 

2)       Достаточность: зададим матрицу  в следующем виде:

                 .

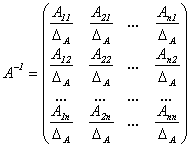Тогда любой элемент произведения   (или ), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны  Таким образом,

               =. Теорема доказана.

 

Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Пример.

Найдем матрицу, обратную к  

следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:

 Не забудем, что алгебраические дополнения к элементам строкиматрицы А образуют в обратной матрице столбец с тем же номером. Итак,  Можно убедиться, что найденная матрица действительно удовлетворяет определению  Найдем

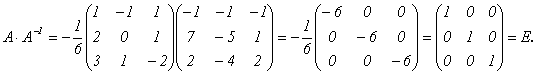
Тот же результат получим и при перемножении в обратном порядке.

 

                  Решение линейных систем с помощью обратной матрицы.

 

Рассмотрим линейную систему (2.3):  и введем следующие обозначения:

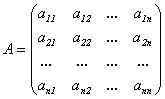- матрица системы, 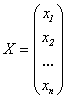- столбец неизвестных,

- столбец свободных членов. Тогда систему (2.3) можно записать в виде матричного уравнения: АХ = В.                                                         (3.1)

Пусть матрица А – невырожденная, тогда существует обратная к ней матрица 

Умножим обе части равенства (3.1) слева на  Получим

                  

Но  тогда , а поскольку          (3.2)

Итак, решением матричного уравнения (3.1) является произведение матрицы, обратной к А, на столбец свободных членов системы (2.3).

 

Пример. Вернемся к системе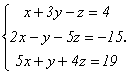 

 Для нее   Найдем :

        Следовательно, 

Таким образом, х = 1, у = 2, z = 3.

Скалярная величина

Скалярная величина (скаляр) – это физическая величина, которая имеет только одну характеристику – численное значение.

Скалярная величина может быть положительной или отрицательной.

Примеры скалярных величин: масса (m), температура (t⁰), путь (S), работа (А), время (t) и т.д.

Математические действия со скалярными величинами – это алгебраические действия.

Векторная величина

Векторная величина (вектор) – это физическая

величина, которая имеет две характеристики – модуль и направление в пространстве.

Примеры векторных величин: скорость (), сила (), ускорение () и т.д.

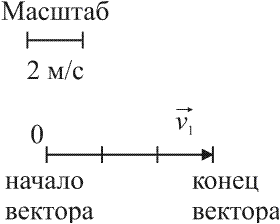
Геометрически вектор изображается как направленный отрезок прямой линии, длина которого в масштабе – модуль вектора.

|| = 6 м/с	|| = 8 м/с

Векторная величина обозначается символом соответствующей физической величины со стрелкой над ней: , , . Модуль вектора обозначается символом без стрелки: || или v.

Действия над векторами подчиняются векторной алгебре. Рассмотрим элементы этой алгебры на примере действий над векторами.

Сравнение векторов

Рассмотрим два вектора и (рис. 44).

Рис. 44

Равные векторы. Два вектора равны, если они имеют:

– равные модули,

– одинаковые направления.

Противоположные векторы. Два вектора противоположны, если они имеют:

– равные модули,

– противоположные направления.

Когда не выполняется одно из условий или оба условия, векторы не равны друг другу.

 

            Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр t.

            Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.

 

Уравнение прямой на плоскости.

 

            Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно, т.е. А² + В²  0. Это уравнение первого порядка называют общим уравнением прямой.

 

            В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

-         C = 0, А  0, В  0 – прямая проходит через начало координат

-         А = 0, В  0, С  0 { By + C = 0}- прямая параллельна оси Ох

-         В = 0, А  0, С  0 { Ax + C = 0} – прямая параллельна оси Оу

-         В = С = 0, А  0 – прямая совпадает с осью Оу

-         А = С = 0, В  0 – прямая совпадает с осью Ох

 

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Расстояние от точки до прямой.

 

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

.

 

            Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:

                                                                                                (1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

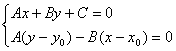
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

            Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

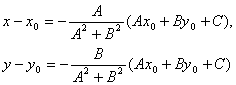
Подставляя эти выражения в уравнение (1), находим:

.

 

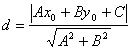Теорема доказана.

 

            Пример. Определить угол между прямыми: y = -3x + 7;  y = 2x + 1.

 

K₁ = -3;   k₂ = 2          tg = ;    = /4.

 

            Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

 

            Находим: k₁ = 3/5,    k₂ = -5/3,  k₁k₂ = -1, следовательно, прямые перпендикулярны.

 

            Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

 

            Находим уравнение стороны АВ: ; 4x = 6y – 6;

2x – 3y + 3 = 0; 

            Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

            Ответ: 3x + 2y – 34 = 0.

 

п.1. Уравнение прямой с угловым коэффициентом.

Пусть дана прямая L на координатной плоскости Оху.

Определение. Углом наклона прямой к оси абсцисс называется уголповорота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.

  

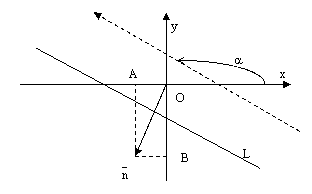
                                              рис.1.

Из определения следует, что угол наклона  прямой L к оси Ох может изменяться от нуля до : . Если прямая , то .

   Пусть

                                                                     (1)

– общее уравнение прямой L, где  – нормальный вектор прямой L и . Тогда  и  (см. рис.1). Выразим у изуравнения (1)

                                    .

                                  , .

Уравнение прямой L принимает вид:

                                            .

Определение. Уравнение прямой вида

                                                                             (2)

называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.

Теорема. В уравнении прямой с угловым коэффициентом

                                            

угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:

                                               .                                (3)

   Доказательство. 1) Если прямая , то  и . С другой стороны, ее нормальный вектор  и .

   Тогда  и, следовательно, , ч.т.д.

2) Пусть , тогда ,  и . Пусть F – точка пересечения прямой L с осью абсцисс. Тогда

                                    , .

Опишем окружность единичного радиуса с центром в точке F , а в точке оси Ох с координатой  проведем касательную m к этой окружности. См. рис.2.

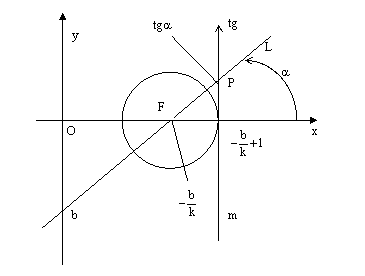
                                                рис.2.

Выберем положительное направление на прямой m, так, чтобы . Тогда ось m является осью тангенсов для данной единичной (тригонометрической) окружности.

   Пусть Р – точка пересечения прямой L с осью тангенсов m. Тогда, с одной стороны, , где  – угол наклона прямой L к оси Ох, а, с другой стороны, точка  и , откуда и следует равенство , ч.т.д.

Теорема доказана.

   Заметим, что приведенное доказательство принадлежит автору этих лекций. Достоинством этого доказательства является то, что оно не зависит ни от величины угла наклона , ни от величины коэффициента .

   В заключение отметим, что коэффициент b в уравнении (2) равен величине отрезка, отсекаемого прямой от оси ординат (см. рис.2).