30) Угол между двумя плоскостями. Взаимное положение плоскостей в пространстве. Расстояние от точки до плоскости.

Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α1 и α2 равен одному из указанных смежных двугранных углов или . Поэтому

Т.к. и , то

Взаимное положение плоскостей в пространстве:

Если плоскости заданы уравнениями

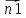= {A₁, B₁, C₁} = {A₂, B₂, C₂}

• Параллельны, и 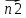коллинеарны, то

• Перпендикулярны, , ┴ , A₁A₂ + B₁B₂ + C₁C₂ = 0

• Пересекаются,

Расстояние от точки до плоскости.

Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:

31) Прямая в пространстве r3. Векторное уравнение прямой. Канонические и параметрические уравнения прямой. Уравнения прямой, проходящей через две точки. Общее уравнение прямой.

Пусть прямая задана т. и 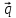= {q₁, q₂, q₃}

Возьмем текущую точку M(x,y,z) прямой l

Тогда = {x – x₀, y – y₀, z – z₀}

||

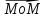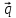
=t

Следовательно, = t – векторное уравнение прямой

x – x₀ = t₁

y – y₀ = t₂

z – z₀ = t₃

x = x₀ + t₁

y = y₀ + t₂ – параметрические уравнения прямой

z = z₀ + t₃

Также : = = – каноническое уравнение прямой

Пусть прямая задается двумя точками: M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂)

= {x₂ – x₁, y₂ – y₁, z₂ – z₁}

M(x, y , z) – текущая точка l

= {x – x₁, y – y₁, z – z₁}

||

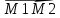
Тогда - уравнение прямой, проходящей через 2 точки

Общее уравнение прямой в пространстве:

Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.

Плоскость в векторной форме может быть задана уравнением:

× + D = 0, где - нормаль плоскости, - радиус- вектор произвольной точки плоскости.

Пусть в пространстве заданы две плоскости, векторы нормали имеют координаты:

(A₁, B₁, C₁), (A₂, B₂, C₂); (x, y, z).

Тогда общие уравнения прямой в векторной форме:

Общие уравнения прямой в координатной форме:

32) Взаимное расположение прямой и плоскости в пространстве r3. Угол между прямой и плоскостью. Условие принадлежности прямой плоскости.

Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке.

Теорема. Пусть плоскость α задана общим уравнением:

а прямая L задана каноническими уравнениями :

или параметрическими уравнениями :

в которых – координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, – координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость в точке, координаты которой можно найти из системы уравнений

(7)

2) если и , то прямая лежит на плоскости;

3) если и ,то прямая параллельна плоскости.

Доказательство. Условие говорит о том, что вектроры n и s не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.

Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.