II. Вычисление производных функции одного аргумента

При вычислении производных применяются следующие правила и формулы:

, с = const,

a = const,

,

, ,

в частности

= 1,

, ,

, ,

,

,

,

,

Пример 11. Найти производную функции

Используя правило дифференцирования произведения и формулы производных и , получим:

Пример 12. Найти производную функции

По правилу дифференцирования частного получаем

Пример 13. Найти производную функции

Применим формулу производной сложной функции. Если бы нужно было вычислить значение при х = х₀, то сначала вычисляли бы 5х₀, затем , затем полученный результат возвели бы в квадрат. То есть является суперпозицией трех функций, поэтому и производная будет равна произведению трех производных

Пример 14. Найти производную функции

Пример 15. Найти производную неявно заданной функции

arctg (x - 2y) + 3y = 2x.

Для дифференцирования функции y = у(x), заданной неявно урав­нением

F(x,y(х)) = 0, существует формула где при вычислении частной производной функции по переменной x, переменная y считается постоянной величиной, а при вычислении частной производной по y , переменная x считается постоянной.

В рассматриваемом примере F (x, y) = arctg (x - 2y)+3y -2x.

,

.

Пример 16. Найти производную функции, заданной параметрически

Для производной функции y (x), заданной параметрически уравнениями

, существует формула .

Для рассматриваемой функции

III. Применение правила лопиталя

Любая из неопределённостей может быть сведена к или , а для раскрытия этих неопределённостей существует правило Лопиталя.

Правило Лопиталя. Если при вычислении предела получается неопределённость или , и существует и равен А, то и предел существует и равен А.

Пример 17. Используя правило Лопиталя, вычислить предел

Подставив вместо нуль, убеждаемся в том, что имеем неопределённость типа . Поэтому можно попытаться применить правило Лопиталя, т.е. найти предел отношения производной числителя данной дроби к производной знаменателя.

.

Можно ещё раз применить правило Лопиталя, а можно вынести в числителе и применить первый замечательный предел.

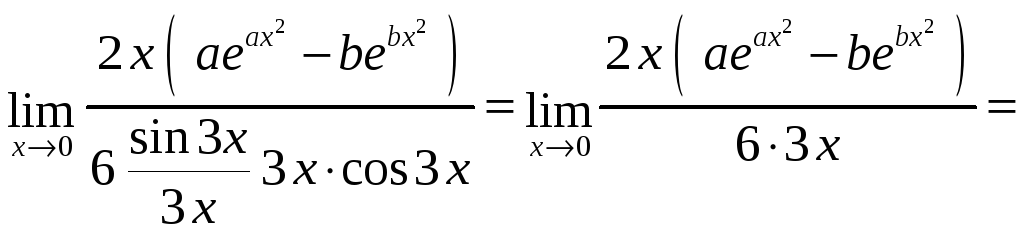
Поскольку предел отношения производных существует, то предел отношения функций также существует и равен полученному значению. То есть,

Пример 18. Найти предел используя правило Лопиталя.

Подставив вместо x единицу, и помня, что , получаем неопределённость .

Её нужно преобразовать к виду или и, лишь потом, применять правило Лопиталя.

Пример 19. Найти предел используя правило Лопиталя.

. Чтобы получить неопределенность или , нужно одну из функций или оставить в числителе, а вторую переместить в знаменатель. Если при применении правила Лопиталя выражение под знаком предела будет усложняться, то нужно вернуться к началу решения и поместить в знаменатель другую функцию.

.

Выражение под знаком предела становится более сложным. Поэтому оставим в числителе другой сомножитель.

IV. Наибольшее и наименьшее значения функции на сегменте

Наибольшее и наименьшее значения функции на сегменте могут достигаться или в экстремальных точках или на концах сегмента. Поэтому, чтобы найти наибольшее и наименьшее значения функции y = f (x) на сегменте [а, b], нужно сделать следующее.

1. Найти производную y' и точки “подозрительные на экстремум”, принадлежащие [a, b]. (Т.е. точки, в которых производная равна нулю или не существует.)

2. Не выясняя вопроса о существовании экстремума в этих точках, вычислить в них значения функции.

3. Вычислить f (a) и f (b).

4. Среди всех полученных значений функции найти наибольшее и наименьшее.

Пример 20. Найти наибольшее и наименьшее значения функции на [1; 5].

Найдём производную y' и точки “подозрительные на экстремум”, принадлежащие [1; 5]:

.

Производная существует на всей числовой оси и равна нулю при x = 0 и x = 4. Точка x=0 не принадлежит [1;5]. Следовательно, единственная точка “подозрительная на экстремум” на сегменте [1;5] – точка x = 4. Вычислим значения функции в этой точке и на концах сегмента.

Итак, наибольшим значением функции на сегменте [1;5] является , а наименьшим