§ 5. Практикум (задачи и решения). Задачи линейного программирования

1. Записать в виде канонической (основной) задачи ЛП следующие задачи:

Решение: Чтобы перейти к ограничениям-равенствам необходимо ввести четыре дополнительные неотрицательные переменные , причем к левым частям неравенств, содержащих знак ≤, дополнительная переменная прибавляется, а из левых частей неравенств, содержащих знак ≥, переменная вычитается. Таким образом, имеем каноническую задачу:

Задачи для самостоятельного решения:

b) c)

2. Записать в виде стандартной (симметричной) следующие задачи ЛП:

a)

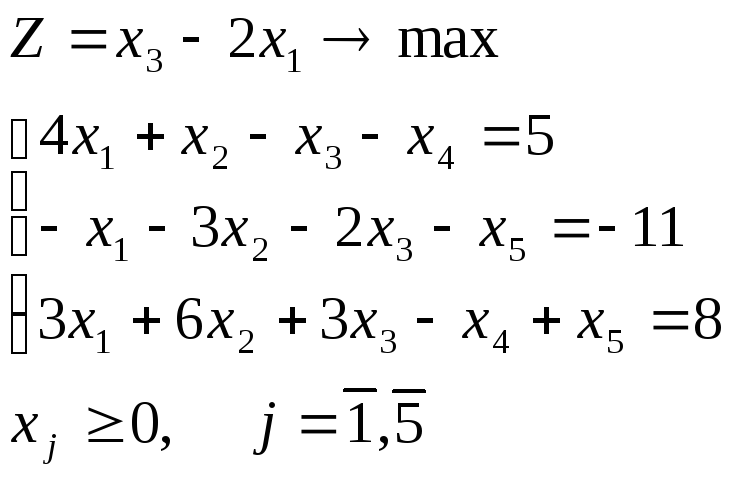
Решение: Используя метод Гаусса, выразим неизвестные через и . Воспользуемся расширенной матрицей системы:

имеем ,

Выразим через и : Получим следующую стандартную задачу ЛП:

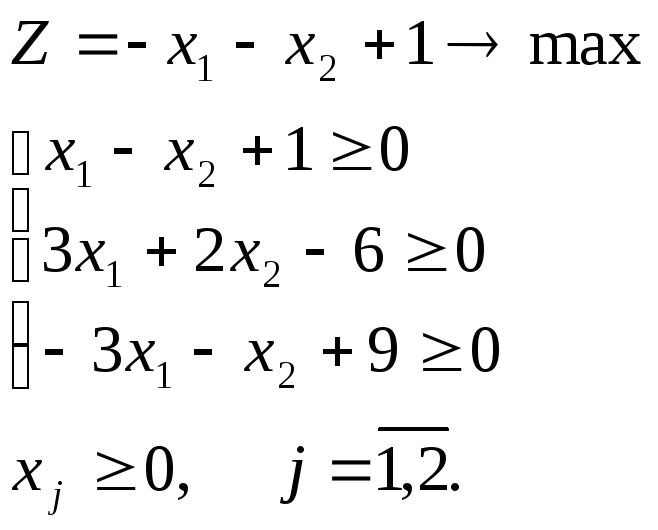
Задачи для самостоятельного решения:

b)

3. Составить двойственные задачи по отношению к следующим задачам ЛП:

a)

Решение: Основная матрица А данной задачи и транспонированная матрица А^Т имеют вид:

Матрица А^Т является матрицей двойственной задачи, число переменных в ней равно числу уравнений в основной задаче, а коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений основной задачи. Таким образом, двойственная задача имеет вид:

Задачи для самостоятельного решения:

b) c)

Геометрическая интерпретация задач линейного программирования

4. Используя геометрическую интерпретацию (графический метод), решить следующие задачи ЛП:

a) Собственник располагает четырьмя видами ресурсов (m=4). Это, например, денежные средства, производственные помещения, оборудование, сырье. Ресурсы необходимо распределить между шестью предприятиями (n=6). Предприятия различаются по экономическим условиям деятельности: месту расположения, системе налогообложения, стоимости энергии, оплате труда и т.д., в связи с чем имеют разные издержки производства. Относительные уровни издержек заданы в таблице.

Относительные уровни издержек на предприятиях

Предприятия	1	2	3	4	5	6
Издержки	0,4	0,5	0,2	0,8	0,6	0,3

Распределение ресурсов по предприятиям сопряжено с необходимостью учета ряда ограничений, которые могут быть описаны системой четырех уравнений с шестью неизвестными:

1–й вид ресурсов 4х₁ + x₄ = 16;

2-й вид ресурсов 2х₂ + х₅ = 10;

3-й вид ресурсов x₃ + 2x₄ + 6х₅ = 76; (4.1)

4-й вид ресурсов 4х₁ + 3х₂ + х₆ = 24;

x_j ≥ 0 (j = 1, 2, …, 4).

Смысл первого уравнения в нашем примере в том, что ресурс вида 1, общий ресурс которого составляет 16 единиц, может размещаться в количестве четырех единиц на предприятии первого типа и одной единицы - на предприятии четвертого типа. Аналогично раскрывается смысл второго и последующих уравнений. Последнее условие говорит о том, что число предприятий не может быть отрицательным.

Необходимо определить, какое количество предприятий каждого типа следует иметь, чтобы общие издержки были минимальными.

В соответствии с таблицей «Относительные уровни издержек на предприятиях» целевая функция, подлежащая оптимизации, примет вид:

у = 0,4x₁ +0,5x₂+ 0,2x₃ + 0,8x₄ +0,6x₅+ 0,3х₆. (4.2)

Решение. Решение задачи сводится к выполнению ограничений, данных уравнениями (4.1), с учетом условия минимизации выражения(4.2).

В нашем примере, когда n - m = 2, каждое из ограничительных линейных уравнений (4.1), а также линейная функция (4.2) могут быть представлены геометрически в двухмерном пространстве (на плоскости).

Чтобы представить ограничения и целевую функцию на графике, необходимо выразить все известные через независимые величины. Например, х₁ и х₂, соответствующие координатным относительно которых будет производиться построение (рис. 4.1).

Из уравнений (4.1) следует: (4.3)

Целевая функция примет вид у = -2,4x₁+0,8x₂ + 22.8 (4.4)

Из сопоставления уравнения (4.3) и последнего из ограничений (4.1) хj> 0 следует:

(4.5)

Рис.4.1

Каждому из неравенств (4.5) на графике рис. 4.1 соответствует полуплоскость, в пределах которой находятся все допускаемые данным неравенством значения переменной величины x_j (j=1, 2, ..., 6).

Так, неравенству x₁ ≥ 0 соответствует полуплоскость вправо от оси х₁ (граница ее заштрихована).

Неравенству x₃ = 8x₁ + 12x₂ - 16 ≥ 0 соответствует полуплоскость вправо и вверх от линии граничного значения данного неравенства (при x₃ = 0). Уравнение этой линии

Таким же образом можно построить границы, определяемые другими уравнениями.

Неравенствам (4.5) соответствует некоторая область-шестиугольник ABCDEF, образованный границами упомянутых выше полуплоскостей. Эта область может быть названа областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям наложенных ограничений (4.1). Из всех допустимых планов нас интересует оптимальный план, при котором функция цели y достигает минимума.

Целевой функции соответствует семейство параллельных прямых. Рассмотрим одну из них, проходящую через начало координат, что будет иметь место при у = 22,8. При этом х₂ = 3x₁.

Интересующая нас прямая у = 22,8, как видно из рис. 4.1, имеет наклон вправо от оси x₂. Задаваясь различными значениями у, получим семейство прямых линий, параллельных прямой у = 22,8, проходящей через точку 0. При этом, чем меньше будет значение у, тем, очевидно, правее будет располагаться соответствующая прямая.

Поскольку мы добиваемся минимального значения у, то нас будет интересовать прямая, расположенная в наибольшем удалении вправо от прямой x=22,8 и проходящая через многоугольник ABCDEF, - прямая у_min.

Единственной точкой, соответствующей оптимальному плану, будет та вершина многоугольника ABCDEF (рис. 4.1), которая одновременно принадлежит области допустимых планов и отвечает требованию минимизации целевой функции у, - вершина C. Из уравнения прямой ВС, проходящей через точку С, следует, что х₁ = 4. Из уравнения прямой DC, проходящей через ту же точку следует, что х₂ = 0.

Подставляя полученные значения х₁ = 4 и х₂ = 0 в уравнение (4.3), определим величины остальных переменных, составляющих оптимальный план:

Таким образом, оптимальный план будет следующим:

(4.6)

Линейная форма (величина издержек) при этом будет минимальной: (4.7)

Задачи для самостоятельного решения:

5. Используя геометрическую интерпретацию (графический метод), решить следующие задачи ЛП:

b) c)d)

e) f)

6. Записать задачу в форме стандартной задачи ЛП и решить её графическим способом:

7. Используя графический метод для двойственной задачи, решить следующую задачу ЛП:

8. На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки 3-х видов в количестве 24, 31 и 18 штук. Каждый лист фанеры может быть разрезан на заготовки двумя способами. В таблице указано количество получаемых заготовок при данном способе раскроя и величина отходов с одного листа фанеры. Сколько листов фанеры, и по какому способу следует раскроить так, чтобы было получено не меньше нужного количества заготовок при минимально возможных отходах.

   Вид заготовок	Количество заготовок при раскрое по способу
   	1	2
   I	2	6
   II	5	4
   III	2	3
   Величина отходов (см2)	12	16

9. Для производства двух видов изделий А и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида приведены в таблице. В ней же указан общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия. Найти оптимальный план выпуска изделий А и В, обеспечивающий максимальную прибыль от их реализации.

Тип оборудования	Затраты времени на обработку одного изделия (станко/час)		Общий фонд полезного рабочего времени (час)
	А	В
фрезерное	10	8	168
токарное	5	10	180
шлифовальное	6	12	144
Прибыль от реализации одного изделия (руб)	14	18