
- •Кластерный анализ
- •2.1. Введение
- •2.2. Признаки объекта
- •2.3. Мера сходства объектов и классов. Расстояния.
- •2.3.1 Метрика Махалонобиса
- •2.3.1.1. Центр класса, дисперсия и среднеквадратичное отклонение
- •2.3.1.2. Скейлинг (масштабное преобразование) и стандартизованное расстояние
- •2.3.1.3 Ковариационная матрица
- •2.3.1.4 Алгоритм вычисления расстояния по Махалонобису
- •2.3.2. Функции сходства.
- •2.3.3 Расстояние между списками
- •2.4. Общая схема классификации и распознавания образов
- •2.4.1. Понятие об обучении. Обучение с учителем и без учителя.
- •2.4.2. Общая схема системы классификации
- •2.5. Разделяющие поверхности и разделяющие функции
- •2.5.1 Линейные и кусочно-линейные разделяющие функции
- •2.6. Методы классификации. Алгоритмы классификации.
- •2.6.1. Алгоритм максимина
- •2.6.2. Алгоритм к-средних
- •2.6.3. Нечеткий алгоритм к-средних (Fuzzy k-means)
- •Алгоритм изодата
2.3. Мера сходства объектов и классов. Расстояния.
В общих чертах, процедура классификации заключается в том, чтобы отнести каждый предъявляемый объект к тому или иному классу. Сами классы могут быть либо заданы заранее, либо могут устанавливаться системой классификации в процессе ее обучения, а именно: в ходе применения решающих правил к некоторому количеству предъявляемых объектов, принадлежность которых к определенному классу уже известна.
Рассмотрим одно исключительно важное понятие, которое будет широко использоваться в дальнейшем при рассмотрении различных методов классификации, а именно: понятие расстояния. Интуитивно ощущается, что понятие расстояния - это наиболее естественное средство оценки того, насколько близки между собой объект и данный класс, два класса, или два объекта. Это связано с тем, что понятие расстояния между объектами и классами отражает степень сходства двух рассматриваемых объектов, если отображать их точками в пространстве существенных признаков. Для определения понятия расстояния в задачах распознавания используется большое число различных математических выражений. Это связано со многими причинами: скорость выполнения вычислительных операций на ЭВМ; в некоторых задачах классификации значения признаков могут быть двоичного типа («да» или «нет») и т. д.
Прежде чем использовать расстояние в качестве меры сходства объектов, рассмотрим следующие понятия.
Метрическим пространством называется
пара
![]() ,
состоящая из множества элементов
,
состоящая из множества элементов
![]() и расстояния
и расстояния
![]() - неотрицательной, однозначной,
действительной функции
- неотрицательной, однозначной,
действительной функции
![]() ,
определенной для всех
,
определенной для всех
![]() и удовлетворяющей трем условиям
(аксиомам):
и удовлетворяющей трем условиям
(аксиомам):
-
 ,
тогда и только тогда, когда
,
тогда и только тогда, когда
 ;
; -
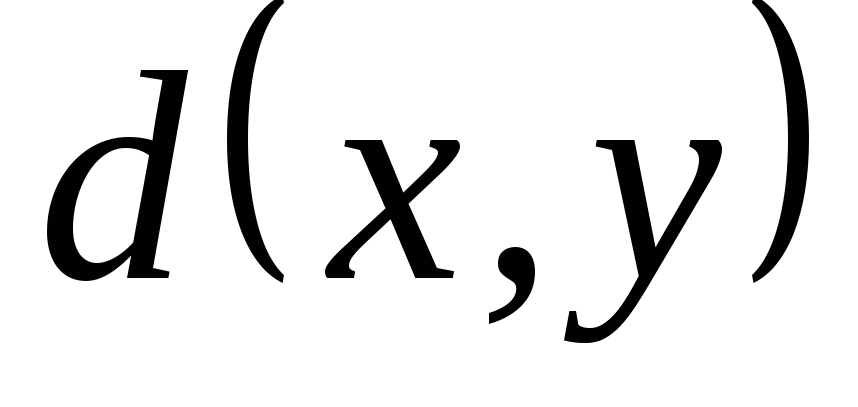 =
= - условие (аксиома) симметричности;
- условие (аксиома) симметричности; -
 - неравенство треугольника.
- неравенство треугольника.
Например, евклидово двумерное пространство
![]() является метрическим, поскольку
расстояние между двумя точками
является метрическим, поскольку
расстояние между двумя точками
![]()
удовлетворяет всем трем условиям, в чем легко убедиться.
Применительно к задачам классификации,
в которых используется расстояние
необходимо рассмотреть еще два важных
понятия, а именно: точных верхней и
нежней граней. Пусть задано некоторое
линейно упорядоченное множество чисел
![]() (множество на котором выполняется
отношение нестрого порядка).
(множество на котором выполняется
отношение нестрого порядка).
Если для рассматриваемого множества
существует такое число
![]() ,
что
,
что
![]() выполняется неравенство
выполняется неравенство
![]() ,
то говорят, что
,
то говорят, что
![]() ограничено сверху числом
ограничено сверху числом
![]() ,
а само это число называют верхней гранью
множества
,
а само это число называют верхней гранью
множества
![]() .
Очевидно, что любое число
.
Очевидно, что любое число
![]() ,
так же является верхней гранью множества
,
так же является верхней гранью множества
![]() .
Другими словами, существует множество
.
Другими словами, существует множество
![]() всех верхних граней множества
всех верхних граней множества
![]()
![]() .
.
Наименьшая из всех верхних граней
называется точной верхней гранью
множества
![]() и обозначается
и обозначается
![]() (читается супремум
(читается супремум
![]() ).
).
Аналогичным образом, множество
![]() может быть ограничено снизу, т.е.
существует такое число
может быть ограничено снизу, т.е.
существует такое число
![]() ,
что выполняется неравенство
,
что выполняется неравенство
![]() ,
которое называют нижней гранью множества
,
которое называют нижней гранью множества
![]() .
.
Наибольшая из всех нижних граней
называется точной нижней гранью множества
![]() и обозначается
и обозначается
![]() (читается инфинум
(читается инфинум
![]() ).
).
Примеры:
-
для множества

 ,
а
,
а
 ,
т.е. точные грани данного множества
являются его элементами;
,
т.е. точные грани данного множества
являются его элементами; -
для множества

 ,
а
,
а
 ,
т.е. точные грани данного множества не
являются его элементами;
,
т.е. точные грани данного множества не
являются его элементами;
Пусть
![]() -
множество классов. Будем называть
расстоянием между объектом
-
множество классов. Будем называть
расстоянием между объектом
![]() и некоторым классом
и некоторым классом
![]() величину
величину
![]() определяемую выражением
определяемую выражением
![]() (2.1)
(2.1)
Расстояние между двумя классами
![]() и
и
![]() определяется величиной
определяется величиной
![]() ,
которая вычисляется аналогичным образом:
,
которая вычисляется аналогичным образом:

 .
(2.2)
.
(2.2)
Как правило, на практике определение расстояния между объектом и классом определяется из соотношения
![]() (2.1а)
(2.1а)
а между классами
 .
(2.2а)
.
(2.2а)
Очевидно, что, чем меньше расстояние между двумя объектами, то тем больше сходство между ними. Это утверждение справедливо лишь в случае «правильно» выбранных признаков, что выполняется далеко не всегда.
Проиллюстрируем это на примере сравнения
двух отрезков, (смотри рис. 2.5.). Отрезки
![]() и
и
![]() имеют разную длину
имеют разную длину
![]() ,
а их проекции на плоскость
,
а их проекции на плоскость
![]() одинаковы. Поэтому, если в качестве
существенных признаков, рассматривать
только проекции этих отрезков на
плоскость
одинаковы. Поэтому, если в качестве
существенных признаков, рассматривать
только проекции этих отрезков на
плоскость
![]() ,
то можно сделать неправильный вывод:
отрезки
,
то можно сделать неправильный вывод:
отрезки
![]() и
и
![]() равны. Что не соответствует действительности.
равны. Что не соответствует действительности.
С другой стороны, установление значений существенных признаков объектов, как правило, связано с различного рода измерениями. Известно, что любая процедура измерений вносит в результат два типа ошибок – систематическую и случайную. Систематическая ошибка обусловлена конструктивными особенностями измерительного прибора (в частности, это может быть точность измерений присущая данному прибору). Например, если измерять расстояние с помощью линейки, то систематическая ошибка по порядку величины будет равна толщине линий деления на линейке (чем толще линия деления, тем больше систематическая ошибка). Случайные ошибки, напротив, связаны с неконтролируемыми факторами, которые оказывают случайное влияние на результаты измерений. Наличие ошибок измерений приводит к тому, что уже нельзя однозначно утверждать к какому из классов относится рассматриваемый объект, можно говорить только о вероятности его принадлежности к тому или иному из классов.
Вернемся к задаче классификации
треугольников. Пусть значения углов
треугольников измеряются с абсолютной
погрешностью
![]() .
Тогда значения углов треугольников
будут определяться из соотношения
.
Тогда значения углов треугольников
будут определяться из соотношения
![]() ,
,
з десь,
десь,
![]() -это
-это
![]() -тое
измерения значения
-тое
измерения значения
![]() -
того угла треугольника. В этом случае,
к примеру, класс равнобедренных
треугольников в пространстве измерений
углов треугольников будет отображаться
уже не точкой, а сферической областью
(см. рис. 2.6.). Таким образом, из-за наличия
ошибок измерений, изменяются и границы
классов.
-
того угла треугольника. В этом случае,
к примеру, класс равнобедренных
треугольников в пространстве измерений
углов треугольников будет отображаться
уже не точкой, а сферической областью
(см. рис. 2.6.). Таким образом, из-за наличия
ошибок измерений, изменяются и границы
классов.
Из этих примеров следует, что выбор существенных признаков, которые обеспечивали бы достоверное распознавание, не всегда легко достигается на практике, и в некоторых случаях приходится прибегать к привлечению других методов, чаще всего – это методы математической статистики, «нечеткие» множества и «нечеткие» вычисления.
В задачах распознавания образов для вычисления расстояния кроме понятия евклидова расстояния, обозначим его
 (2.3)
(2.3)
используются
и ряд других соотношений. В общих чертах,
это связано с тем, что при вычислении
расстояния
![]() используется достаточно большое
количество операций, что может существенно
увеличить время обработки данных на
ЭВМ, и, следовательно, автоматизированная
система классификации может оказаться
не эффективной, для использования в
реальных условиях. Поэтому, с одной
стороны, специально для уменьшения
количества операций и повышения
быстродействия вычислений на ЭВМ были
и предложены другие определения понятия
«расстояние». Другой важный момент,
определяющий выбор той или иной метрики,
связан с тем, что в одной метрике классы
могут быть пересекающимися, а в другой
нет. Приведем некоторые из них, которые
используются для вычисления расстояния
в задачах классификации:
используется достаточно большое
количество операций, что может существенно
увеличить время обработки данных на
ЭВМ, и, следовательно, автоматизированная
система классификации может оказаться
не эффективной, для использования в
реальных условиях. Поэтому, с одной
стороны, специально для уменьшения
количества операций и повышения
быстродействия вычислений на ЭВМ были
и предложены другие определения понятия
«расстояние». Другой важный момент,
определяющий выбор той или иной метрики,
связан с тем, что в одной метрике классы
могут быть пересекающимися, а в другой
нет. Приведем некоторые из них, которые
используются для вычисления расстояния
в задачах классификации:
1.
![]() -
расстояние по Манхэттену («метрика
городских кварталов»)
-
расстояние по Манхэттену («метрика
городских кварталов»)
![]() (2.4)
(2.4)
2.
![]() -
Чебышевское расстояние
-
Чебышевское расстояние
![]() (2.5)
(2.5)
В этих выражениях
этих выражениях
![]() и
и
![]() -
векторы существенных признаков объектов,
между которыми вычисляется расстояние,
а
-
векторы существенных признаков объектов,
между которыми вычисляется расстояние,
а
![]() - значение
- значение
![]() -того
признака
-того
признака
![]() -го
объекта.
-го
объекта.
В
метрическом пространстве объекты,
принадлежащие одному классу, занимают
определенную область. Поверхность,
которая охватывает эту область, называется
разделяющей поверхностью, так как она
разделяет это пространство на отдельные
области-классы. Такая поверхность
представляет собой геометрическое
место точек удовлетворяющих уравнению
![]() .
На плоскости это уравнение, в общем
случае, определяет некоторую кривую.
.
На плоскости это уравнение, в общем
случае, определяет некоторую кривую.
В
качестве примера таких разделяющих
линий на плоскости
![]() рассмотрим геометрическое место точек,
равноудаленных от начала координат на
расстояние, равное единице в различных
метриках (рис. 2.7). Для трех вышеприведенных
определений расстояния получим:
рассмотрим геометрическое место точек,
равноудаленных от начала координат на
расстояние, равное единице в различных
метриках (рис. 2.7). Для трех вышеприведенных
определений расстояния получим:
X2 X2 X2![]()
Рассмотрим еще один способ вычисления расстояний: расстояние в метрике Камберра
![]() (2.6.)
(2.6.)
Геометрическое место точек, равноудаленных
от заданной, для
![]() будет изменяться в зависимости от
выбранной опорной или базовой точки.
Например, геометрическое место точек
на плоскости, удаленных на расстояние
будет изменяться в зависимости от
выбранной опорной или базовой точки.
Например, геометрическое место точек
на плоскости, удаленных на расстояние
![]() от опорной точки
от опорной точки
![]() с координатами
с координатами
![]() ,
задается уравнением
,
задается уравнением
![]()
Р ассмотрим
частный случай
ассмотрим
частный случай
![]() .
Тогда геометрическое место точек,
удаленных на расстояние, равное 1, от
опорной точки с координатами
.
Тогда геометрическое место точек,
удаленных на расстояние, равное 1, от
опорной точки с координатами
![]() можно определить по формуле (см. рис.
2.8)
можно определить по формуле (см. рис.
2.8)
![]()
Для конкретного случая классификации объектов, выбирают ту или иную метрику с тем, чтобы с одной стороны уменьшить вычислительную сложность задачи классификации, а, с другой стороны, выбранная метрика должна обеспечивать «наилучшее» разбиение на классы.
П роиллюстрируем
последнее утверждение на простом примере
(см. рис. 2.9.). Как видно из рисунка, классы
в метрике Евклида являются пересекающимися,
что существенно усложняет классификацию
объектов. В таком случае лучше использовать
метрику Чебышева, которая позволяет
достаточно просто разбить множество
существенных признаков на сепарабельные
классы, и тем самым обеспечить эффективную
и достоверную классификацию объектов.
роиллюстрируем
последнее утверждение на простом примере
(см. рис. 2.9.). Как видно из рисунка, классы
в метрике Евклида являются пересекающимися,
что существенно усложняет классификацию
объектов. В таком случае лучше использовать
метрику Чебышева, которая позволяет
достаточно просто разбить множество
существенных признаков на сепарабельные
классы, и тем самым обеспечить эффективную
и достоверную классификацию объектов.
