2.6.3. Нечеткий алгоритм к-средних (Fuzzy k-means)

Процедуру алгоритма К-средних часто называют «четкой» классификацией. В этом алгоритме каждый объект выборки либо принадлежит, либо не принадлежит к определенному классу. Алгоритм К-средних может успешно применяться в случае непересекающихся классов, т.е. в случае, когда между классами можно провести четкие границы. В противоположность этому нечеткий алгоритм К-средних реализует «мягкую» или «нечеткую» классификацию и используется в тех случаях, когда не представляется возможным однозначно установить принадлежность объекта к определенному классу. В этом случае говорят, что каждый объект может иметь определенную степень принадлежности к каждому из классов. Например, объект может принадлежать на 20% к первому классу, на 65% ко второму и на 15% к третьему классу, а объект - на 70% к первому, на 10% ко второму и на 20% к третьему.

Нечеткий алгоритм К-средних широко применяется для распознавания и классификации объектов с «нечеткими» признаками, например, в системах компьютерной обработки и распознавания цветных изображений, географии и геодезии при классификации почв и ландшафтов, метеорологии при предсказаниях изменений климата и др.

Идея нечеткого алгоритма К-средних основана на минимизации суммарной взвешенной среднеквадратичной ошибки

(2.24)

при следующих условиях:

для любого ;

для любого ; (2.25)

для любых и .

Здесь – количество объектов в выборке; – количество классов; - «функция принадлежности», т.е. функция, значение которой равно степени принадлежности -го объекта к -му классу; - квадрат расстояния между -м объектом и центром -го класса в выбранной метрике (в дальнейшем эту величину будем обозначать просто ) .

Параметр в показателе степени в (2.24) определяет собой «степень нечеткости», «степень размытия» классов, или степень перекрытия классов в конечном решении задачи классификации. При получится “четкая” классификация, а при решение приближается к максимальной степени нечеткости. Выбор параметра достаточно произволен и при использовании данного алгоритма обычно требуется многократно провести процедуру классификации для различных , а затем выбрать наилучший результат. Однако следует иметь ввиду, что очень большие значения приводят к тому, что каждый объект будет иметь одинаковую степень принадлежности ко всем классам и классы станут вообще неразличимы. Кроме того, при использовании различных метрик наилучшие результаты будут получаться при различных значениях параметра . Так, например, для метрики Евклида вначале рекомендуется выбирать , а для метрики Махаланобиса вначале нужно взять меньшее значение .

Минимизация функции с использованием условий (2.25) приводит к следующему выражению для функции принадлежности :

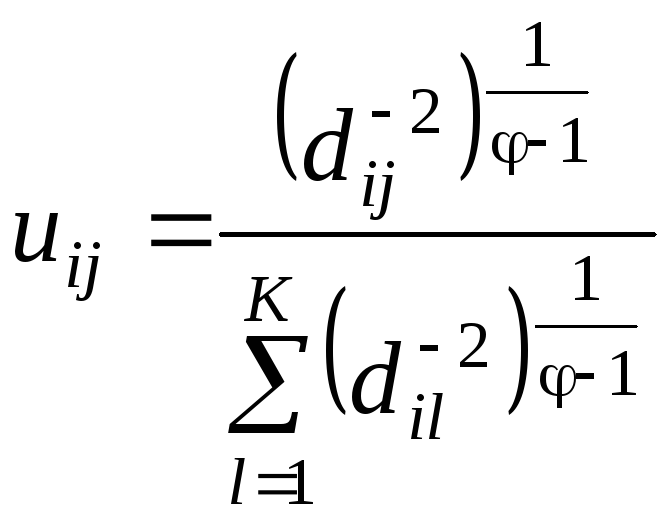для всех и . (2.26)

Тогда положения центров классов вычисляются следующим образом:

для всех . (2.27)

Перейдем теперь непосредственно к изложению словесного описания нечеткого алгоритма К-средних.

1. Зададим количество классов , значение для параметра нечеткости () и выберем метрику для вычисления расстояний в пространстве существенных признаков.

2. Задать точность вычислений . Этот параметр используется для прекращения вычислений. Если положения центров всех классов на некоторой итерации изменились по сравнению с их положениями на предыдущей итерации на величину, меньшую , то вычисления заканчиваются.

3. Задать максимально допустимое число итераций . Этот параметр также используется для прекращения вычислений. Если требуемая точность еще не достигнута, но количество проведенных итераций стало равно , то вычисления прекращаются, и выводится сообщение о невозможности достигнуть заданной точности при данном числе итераций . Зададим начальное значение счетчика итераций .

4. Выбираем начальные положения центров классов . Как и в «четком» алгоритме К-средних в качестве можно выбрать первых объектов выборки, т.е. , и т.д., либо случайным образом выбрать произвольных объектов.

5. Вычисляем все компоненты функции принадлежности по формуле

.

Для этого нужно предварительно вычислить в выбранной метрике квадраты расстояний между всеми объектами и всеми центрами классов, т.е. величины для всех и . Если какая-либо из величин или , где некоторое наперед заданное положительное число , то для данных и следует положить .

6. Вычислив компоненты функции принадлежности для всех объектов, распределяем их по классам. Объект принадлежит к классу , если 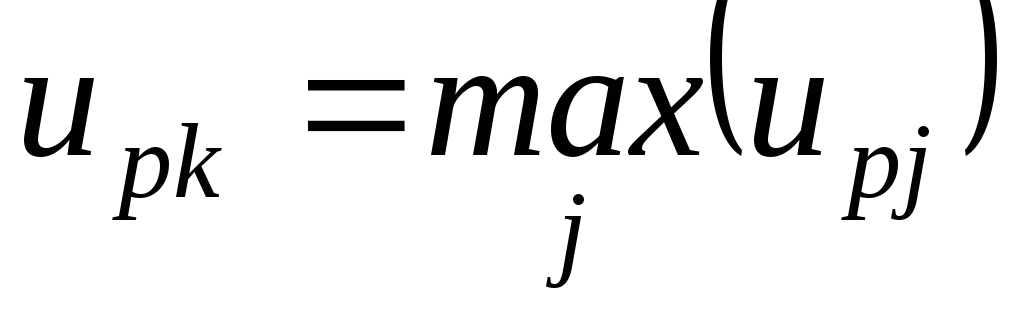, то есть значение функции принадлежности объекта для данного класса наибольшее.

7. Увеличим счетчик итераций на единицу . Вычислим новые положения центров классов по формуле

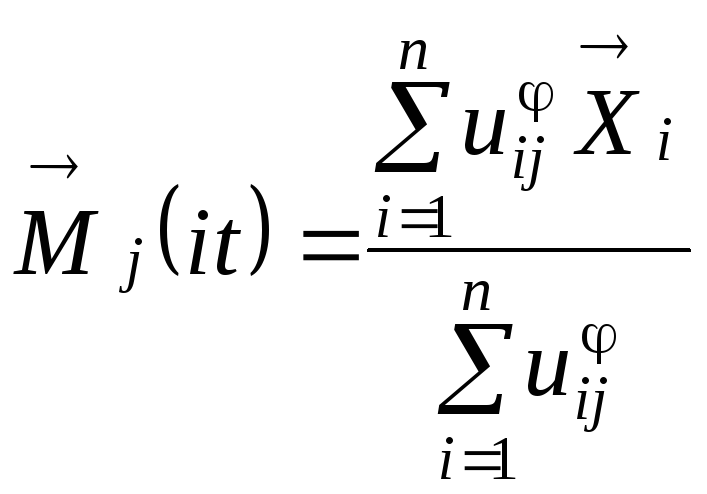для всех .

Для вычисления центров классов используется функция принадлежности , вычисленная на шаге 5.

8. Вычислим расстояние между положением центра класса на данной и предыдущей итерации для всех центров, т.е. величины для всех .

9. Если , то вычисления закончены с выводом дополнительного сообщения о невозможности достигнуть заданной точности при данном .

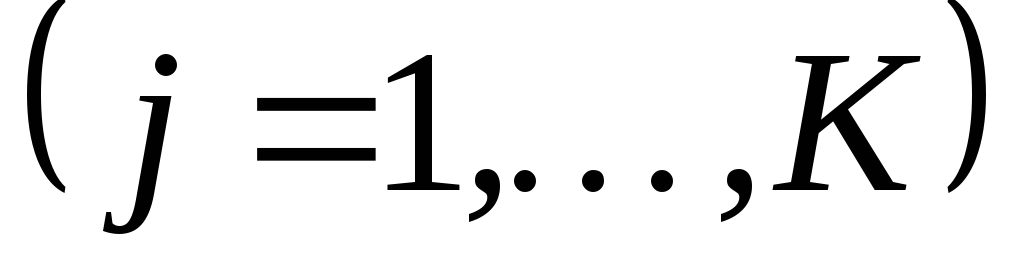10. Если , то вычисления закончены, иначе перейти к шагу 5.

Результатом выполнения алгоритма является функция принадлежности - матрица , которая содержит данные о степени принадлежности -го объекта к -му классу. Пусть, например, для пяти объектов и трех классов эта матрица имеет вид:

j i	1	2	3
1	0,78	0,15	0,07
2	0,92	0,08	0,00
3	0,15	0,05	0,8
4	0,00	0,05	0,95
5	0,09	0,87	0,04

Естественно считать, что объект принадлежит к тому классу для которого функция принадлежности имеет максимальное значение. Таким образом, для данного случая первый объект принадлежит к первому классу ; второй объект принадлежит к первому классу; третий объект принадлежит третьему классу и т.д.