2.6.2. Алгоритм к-средних
Для систем автоматической классификации является характерным то, что предполагается заранее известным либо количество классов, либо объекты – представители классов. Для реализации систем автоматической классификации, при известном или заданном количестве классов, используется алгоритм К-средних.
Алгоритм К-средних отличается от
алгоритма Максимина, в первую очередь
тем, что заранее известно или задано
количество классов
.
В качестве представителей этих классов
могут использовать либо
первых элементов из обучающей выборки,
либо любые
элементов. Классификации в этом случае
заключается в поиске центров заданного
количества классов
.
Установив центры классов необходимо
провести первый этап классификации,
который заключается в распределении
объектов обучающей выборке по заданным
классам по принципу наименьшего
расстояния. Это означает, что объект
относят к тому классу, для которого
является наименьшим. Распределив все
объекты обучающей выборки по классам,
находят новые центры классов. Новые
положения центров классов в пространстве
существенных признаков определяют из
условия минимума среднеквадратического
отклонения объектов данного класса от
его центра
здесь
-
вектор соответствующий центру
-го
класса.
Отсюда следует что положение центра
-того
класса определяется из соотношения
.
Тогда получим, что
,
здесь
-
количество объектов в
-
том классе. Другими словами, центр класса
– это средний вектор объектов принадлежащих
данному классу.
Определив новые положения центров всех классов, повторяют процедуру распределения объектов по классам. Определение новых положений центров классов и распределение объектов по классам с новыми центрами продолжают до тех пор, пока положения центров классов не перестанут изменяться.
Рассмотрим словесное описание алгоритма К–средних. Он состоит из следующих шагов.
-
Задать количество классов
и параметр
.
-
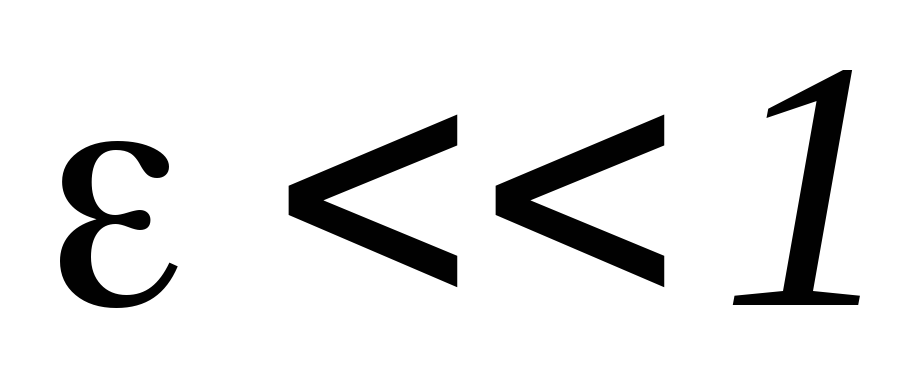На первой итерации (
)
выбирают в качестве экземпляров классов
первые
элементов обучающей выборки:
-
Распределить объекты обучающей выборки по классам. Классы формируют следующим образом. Пусть необходимо установить к какому из классов принадлежит объект
.
Вычислим расстояния между данным
объектом и центрами классов в выбранной
метрике (например, пусть это будет
метрика Евклида)
.
Здесь
-количество
существенных признаков,
- существенный признак или
-ая
координата объекта в пространстве
существенных признаков,
-
координаты центра
-го
класса. Во множестве расстояний
найдем наименьшее из них
,
запомним соответствующий номер класса
-
.
Отнесем объект
к классу с номером
.
Классы считаются сформированными, если
обработаны все объекты обучающей
выборки.
-
Положить
и вычислить новые положения центров
классов
,
то есть для определения новых центров
классов необходимо вычислить
средних значений (отсюда и происходит
название алгоритма).
-
На этом шаге используется процедура, которая позволяет установить окончание алгоритма (окончание процесса обучения системы классификации). Для этого необходимо вычислить расстояния в выбранной метрике между центрами одноименных классов на
-ой
и
итерациях
.
Если при этом выполняется условие
,
то есть отклонение новых положений центров классов лежит в пределах заданной точности вычислений, то алгоритм закончен. В противном случае, когда
нужно вернуться к шагу 3.
Рассмотрим
реализацию этого алгоритма на примере,
когда количество объектов равно
,
а количество существенных признаков
равно
.
Для
удобства вычислений будем использовать
четыре таблицы. Первая – это таблица
значений существенных признаков объектов
(номер строки – номер объекта номер
столбца – номер существенного признака).
Следует отметить, что при разработке
программного обеспечения реализующего
систему классификации на базе алгоритма
К-средних, каждая из таблиц в программе
заменяется соответствующим массивом.
-
Y(i,j)
1
2
1
4
12
2
4
14
3
13
11
4
16
14
5
6
4
6
7
4
Вторая таблица – таблица пометок объектов. Если объект – это центр класса, то ему присваивают отрицательную пометку (номер класса с отрицательным знаком) или положительную пометку равную номеру класса, к которому отнесён данный объект.
-
Pm(i)
1
2
3
4
5
6
Третья таблица - это расстояния в выбранной метрике между координатами центров классов и непомеченными объектами.
-
d(i,j)
№ об.
№ кл.
1
2
3
4
5
6
1
2
3
Четвертая таблица – координаты центров классов.
-
N(i,j)
j
i
1
2
1
2
3
Зададим
желаемое число классов
и параметр
.
Выберем в качестве экземпляров первого,
второго и третьего класса соответственно
первый, второй и третий объекты обучающей
выборки.
-
N(i,j)
j
i
1
2
1
4
12
2
4
14
3
13
14
и присвоим им отрицательные пометки в таблице пометок
-
Pm(i)
1
2
3
4
5
6
-1
-2
-3
Вычислим расстояние между центрами классов и всеми непомеченными объектами (в метрике Манхэттена).
-
d(i,j)
1
2
3
4
5
6
1
14
10
11
2
12
12
13
3
6
14
13
Найдем
минимальные расстояния между центрами
классов и всеми непомеченными объектами,
т.е. минимальные значения в каждом
столбце таблицы
.
Классифицируем объекты по критерию
минимального расстояния и заполняем
таблицу пометок:
следовательно объект
принадлежит классу
.
В итоге получим
-
Pm(i)
1
2
3
4
5
6
-1
-2
-3
3
1
1
Здесь
объекту с номером
присваивается положительная пометка,
равная номеру класса, расстояние до
которого от данного объекта минимально.
Вычислим
новые значения координат центров. С
этой целью поставим в соответствие всем
объектам каждого класса, включая центры,
векторы в пространстве существенных
признаков. Например, для первого класса
это будут векторы
,
и
.
Новое положение центра первого класса
вычисляется по формуле
.
В координатном представлении:
.
Поступая
аналогичным образом, найдем центры
оставшихся классов:
и
.
Найдем расстояния между новыми и предыдущими центрами одноименных классов:
,
и
.
Найдем
наибольшее из них
.
Поскольку
,
то необходимо повторить процедуру
распределения объектов по классам с
новыми центрами. Для этого необходимо
выполнить следующие действия. Поскольку
положения центров первого и третьего
классов изменилось, то изменим знаки
их пометок:
и
.
Для второго центра координаты не изменились, поэтому его пометку не изменяем.
-
Pm(i,j)
1
2
3
4
5
6
1
-2
3
3
1
1
Занесем новые координаты центров в соответствующую таблицу.
-
N(i,j)
j
i
1
2
1
6
7
2
4
14
3
15
13
Обнуляем все положительные пометки. В данном случае таблица пометок примет вид:
-
Pm(i,j)
1
2
3
4
5
6
0
-2
0
0
0
0
Вычисляем расстояния между центрами классов и непомеченными объектами
-
d(i,j)
1
2
3
4
5
6
1
7
11
17
3
4
2
2
12
12
12
13
3
12
4
2
18
17
Находим наименьшие расстояния в столбцах этой таблицы. Классифицируем объекты и заполняем таблицу пометок
-
Pm(i)
1
2
3
4
5
6
2
-2
3
3
1
1
Вычисляем
новые координаты центров
,
,
,
сравниваем их с предыдущими значениями.
Положение центра
изменилось и его предыдущая пометка
отрицательная, поэтому изменим ее
знак:
.
-
Pm(i)
1
2
3
4
5
6
2
2
3
3
1
1
Заносим координаты новых центров в таблицу, если они изменились
-
N(i,j)
1
2
1
7
4
2
4
13
3
15
13
Координаты центров поменялись, выполняем следующую итерацию. Обнуляем все положительные пометки.
-
Pm(i)
1
2
3
4
5
6
0
0
0
0
0
0
Вычисляем расстояния от новых центров классов до всех объектов
-
d(i,j)
1
2
3
4
5
6
1
11
13
13
19
1
0
2
1
1
11
13
11
12
3
12
12
4
2
18
17
Классифицируем объекты:
-
Pm(i)
1
2
3
4
5
6
2
2
3
3
1
1
Вычисляем координаты новых центров и сравниваем их с предыдущими значениями.
-
N(i,j)
1
2
1
7
4
2
4
13
3
15
13
Поскольку координаты центров не изменились, то алгоритм закончен. Таблица пометок содержит всю информацию о распределении объектов между классами.