Определение устойчивости по критерию Гурвица:

Из характеристического уравнения имеем

а₀=2, а₁=65, а₂=425, а₃=1250, а₄=5568,75

А1 = а₁ = 65

–главный определитель Гурвица

a₀=2, 65,25130,7878000,43870000000

Определители Гурвица низшего порядка имеют тот же знак, что и a₀, следовательно, система устойчива.

Определение устойчивости по критерию Михайлова:

D(p)= =0 – характеристическое уравнение системы

Подставляем p=j и находим вещественную и мнимую функции Михайлова:

X()=2⁴–425²+5568,75=0

Y()=(–65²+1250)=0

Корни уравнения Y()=0 ₁=0, ₂=4,385

Корни уравнения X(ω)=0 ω₁=14,03 ω₂=198,47

а) б)

Рис.4 - Годограф Михайлова.

Согласно критерию Михайлова , для устойчивости системы автоматического регулирования необходимо и достаточно, чтобы годограф характеристического вектора D(p), где , начинаясь прина действительной оси, с ростомотобходил последовательно, следуя против часовой стрелки, 4 квадранта, нигде не обращаясь в ноль.

Кривая проходит через четыре квадранта, и при этом вектор D(p) нигде не обращается в ноль, значит система устойчива.

Определение устойчивости по критерию Найквиста:

–передаточная функция разомкнутой цепи

Заменив p на j, получаем

откуда

Рис.5 – АФЧХ разомкнутой системы

По критерию Найквиста, для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы при измененииотне охватывал точку (-1;j0).

Построив годограф, мы видим, что он не огибает точку (–1; j0), следовательно, по критерию Найквиста система устойчива.

Запасы устойчивости по амплитуде и по фазе.

Рис.6 - АФЧХ разомкнутой системы

Запас устойчивости по амплитуде 0.25( отрезок, заключенный между точкой (–1; j0)

запас по устойчивости по фазе =22.72

5. ЛАХ разомкнутой исходной системы, желаемая ЛАХ,

ЛАХ и передаточная функция корректирующего устройства.

W_раз(p)= , откуда

T₁=0.2, T₂=0.04

₁=5 ₂=25

lg₁=0.69 lg₂=1.39

K₁=33,3

, (10)

. (11)

Первая низкочастотная асимптота до частоты ₂ имеет наклон –20 дБ/дек, от ₂ до ₃ наклон –40 дБ/дек, от ₃–60 дБ/дек.

Графики ЛАЧХ и ЛФЧХ даны в приложении.

Построение желаемой лачх с учетом требуемых значений быстродействия, перерегулирования и точности.

Построение желаемой ЛАЧХ производится из следующих условий быстродействия, перерегулирования и точности: σ=20%, t_р=2 c.

Требуемое значение запаса по модулюдБ и запаса по фазе.

Из полученных условий строим желаемую ЛАЧХ. Отметим точку и проведем через нее прямую с наклоном –20дБ/дек, которая представляет собой среднечастотную амплитуду желаемой ЛАЧХ. Продолжим прямую до тех пор, пока ординаты не станут равными L₁ и L₂. Этим точкам соответствуют частоты и:,. Из этих данных определяем,. Низкочастотная область желаемой ЛАЧХ совпадает с исходной ЛАЧХ:.

Высокочастотную область проводят так, чтобы через каждую 0,2 дек ломать на 20 дБ/дек, чтобы наклон желаемой ЛАЧХ в конце совпало с исходной ЛАЧХ: Она представлена в приложении.

Составим передаточную функцию разомкнутой системы для желаемой САУ, получим:

. (11)

После этого построим ЛФХ желаемой системы (см. приложение) и определим запасы устойчивости по амплитуде и по фазе, и сравним их с запасами устойчивости, полученными из номограммы.

,

Запас по фазе , запас устойчивости по амплитуде равен. Требуемые запасы выполняются.

График желаемой ЛАЧХ представлен в приложении.

6. Построение ЛАЧХ корректирующего устройства, нахождение его передаточной функции, расчет параметров.

Выбираем последовательное включение корректирующего устройства в прямую цепочку САУ.

Рис.7 - Схема включения корректирующего устройства в исходную систему.

ЛАЧХ корректирующего устройства получается вычитанием ординат L_исх(w) из L_жел(w).

По графику полученной ЛАЧХ (приложение) находим сопрягающие частоты:

Передаточная функция корректирующего устройства имеет вид:

Корректирующее устройство можно представить в виде последовательных динамических звеньев, разделенных усилителями.

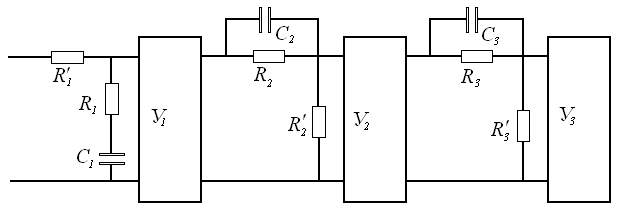
Рис.8 - Схема корректирующего устройства

Рассчитаем параметры каждого звена.

1 звено – интегрирующее. Его передаточная функция имеет вид:

Так как

То мкФ

кОм

кОм

2 звено – дифференцирующее. Его передаточная функция имеет вид:

Так как

То мкФ

кОм

кОм

Коэффициент передачи

3 звено также является дифференцирующим. Его передаточная функция имеет вид:

Параметры находятся аналогично 2 звену.

мкФ

кОм

кОм

Коэффициент передачи

Рассчитаем параметры усилителя.

Необходимо, чтобы коэффициент передачи исходной системы сохранялся, поэтому

Пусть , тогда

Передаточная функция скорректированной системы находится по формуле

Тогда

7. Статическая, скоростная и по ускорению ошибки исходной и скорректированной систем. Запасы устойчивости по амплитуде и фазе.

Статическая, скоростная и по ускорению ошибки.

Передаточная функция ошибки замкнутой системы вычисляется по формуле:

Тогда для исходной системы

W_исх(p) =

Статическая ошибка:

Скоростная ошибка:

Ошибка по ускорению:

Для скорректированной системы

Статическая ошибка:

Скоростная ошибка:

Ошибка по ускорению:

Для скорректированной системы коэффициенты ошибок значительно меньше, чем для исходной.