
курсовая работа / KP_Fox
.DOC



БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА УИТ
КУРСОВАЯ РАБОТА
по дисциплине
Теория автоматического управления
Исследование устойчивости стационарных и нестационарных линейных и непрерывных и дискретно-непрерывных систем автоматического управления
Выполнил ст. гр. УИТ-41
Удалов C.В.
Принял доцент каф. УИТ
Скоробогатова Т.Н. _______
“______” ___________2003
2003

СОДЕРЖАНИЕ
Часть 1 Линейная САУ
1 Техническое задание
2 Упрощение структурной схемы САУ
3 Анализ устойчивости САУ
4 Построение переходных характеристик
5 Анализ качества управления
Часть 2 Нелинейная САУ
1 Техническое задание
Вывод
Список используемой литературы
Вариант № 19
ЧАСТЬ 1
1 Техническое задание
Исходная схема САУ изображена на схеме 1
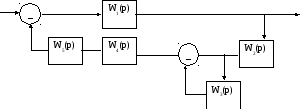
Схема 1
Передаточные функции звеньев:
W1(p)=![]() ;
;
W2(p)=
![]() ;
;
W3(p)=![]() ;
;
W4(p)=1,4147;
W5(p)=
![]() ;
;
2 Упрощение структурной схемы САУ
Проведя преобразования, получим схему 2.
W1(p)
W2(p)
W7(p)
W6(p)






Схема 2
Упростим:
W6(p)=W4(p)· W5(p)
W 7(p)=
7(p)=![]()
W8(p)= W2(p)· W6(p) W7(p)
W(p)=
![]()
Упростим:
W(p)=![]() =
=

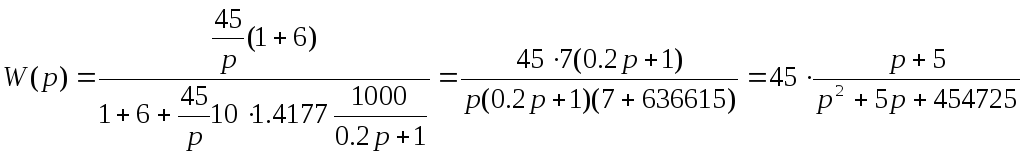
3 Анализ устойчивости САУ
Запишем характеристическое уравнение системы:
![]()
a0=1; a1=5; a2=454725;
Теперь можно составить главный определитель Гурвица
![]()
Теперь посчитаем определители:
1.
![]()
2.
![]()
Согласно критерию Гурвица, система устойчива, т.к. определители имеют один знак с a0=1
4 Построение переходных характеристик
Для большинства характеристик потребуется определить вещественную и мнимую части комплексной передаточной функции, что и проделаем.
Исходная передаточная функция имеет вид:
![]()
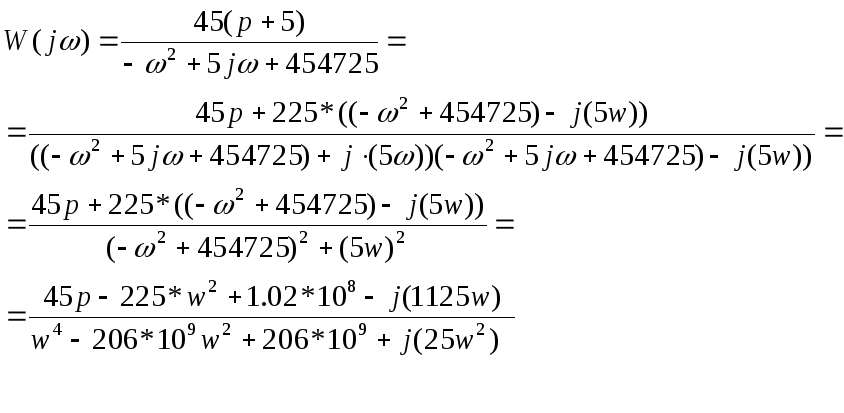
Соберем коэффициенты и выделим вещественную и мнимую части.
![]()
![]()
![]()
![]() =
=![]()
4.1 Построение АЧХ
АЧХ системы
определяется по формуле
![]()
Исходя из представленных формул АЧХ примет вид:
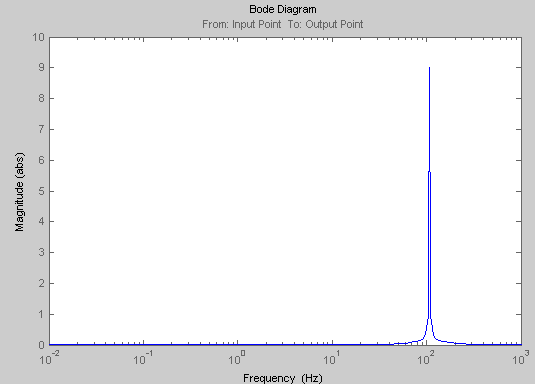
График 1
4.2 Построение ФЧХ
Фазовая характеристика находится по формуле:
![]()
График 2
4.3 Построение АФЧХ, ЛАЧХ и ЛФЧХ системы
Построение АФЧХ заключается в отображении на координатных осях U(ω) и V(ω).
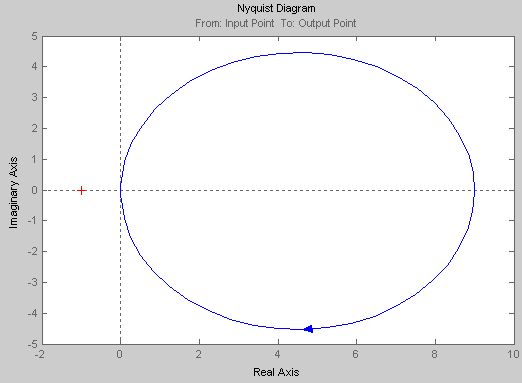
График 3
Актуализируем участок (-1;0)

График 4
Совместное построение ЛАЧХ и ЛФЧХ
ЛФЧХ есть ФЧХ рассматриваемая как функция ln(ω)

График 5
Суммируя данные из графиков 4 и 5, определим:
запас устойчивости по фазе составляет γС=
запас устойчивости по амплитуде LЗАП=134 дБ
4.4 Построение графика переходного процесса
Переходный процесс в системе, это реакция на единичное ступенчатое воздействие
Передаточная функция системы записывается как:
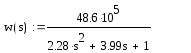
По данной переходной функции построим переходную характеристику (график 6)

График 6
5 Анализ качества управления
Используя график 6, определим следующие величины:
1) Установившееся значение hУСТ=4.756*106
2) Время переходного процесса tП=13.7 c
3) Перерегулирование
![]()
4) Период колебаний Т=∞
5) Частота колебаний ω=0
6) Колебательность n=0
7) Время нарастания регулируемой величины tН=∞
8) Время первого согласования tПС=∞
Это мы определили прямые оценки качества, теперь определим косвенные оценки качества, которые проводятся по амплитудно-частотной характеристики
ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ САУ
1 Техническое задание
Рисунок нелинейной САУ приведена на рисунке
W1(p)



W2(p)
W4(p)
W5(p)






W3(p) NE

Передаточные функции звеньев:
W1(p)=![]() ;
;
W2(p)=
![]() ;
;
W3(p)=![]() ;
;
W4(p)=1,4147;
W5(p)=
![]() ;
;
График, описывающий нелинейный элемент NLE приведен на рис.
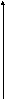 y
y

 1000
1000
 0
0
x
 -1000
-1000
2 Упрощение структурной схемы САУ
Разорвем цепь перед нелинейным элементом и получим схему
NLE
W6(p)
W7(p)
W1(p)
W3(p)
W2(p)
W4(p)
W5(p)









В цепи рисунка можно четко выделить линейную и нелинейную части, преобразуем его.

Обозначение: W8(р)= W6(p)·W7(p)· W1(p)·W2(p)·W3(p)·W4(p) ·W5(p)
Передаточная функция линейной части запишется в виде
![]()
3 Построение фазового портрета
Передаточная
функция есть
![]() или
или
![]() .
Получим:
.
Получим:
![]()
Приведем к виду:
(![]() )*x=
)*x=
![]() *x1
*x1
Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.
Введем замену pix=yi и исключим из правой части уравнения производную
Получим систему уравнений:
Для участка [-∞;0] и [0;+∞]:
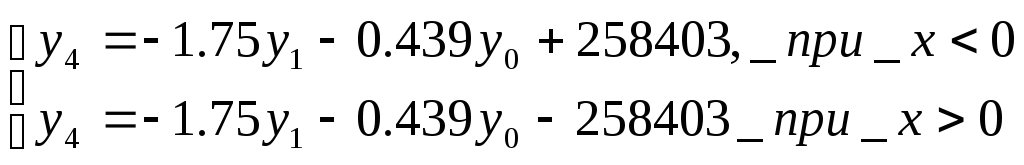
Создадим матрицу для решения дифференциального уравнения:

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:
![]()
Возьмем количество
точек равным 1000 и конечное время
интегрирования 100, то матрица решений
запишется как:
![]() .
.
По введенным данным получим фазовый портрет
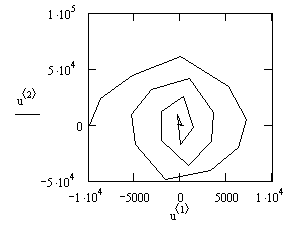
Вывод: на рисунке представлен фазовый портрет нелинейной системы. Это типовой вид кривой. До перехода через точку 0 работает первое уравнение системы, при переходе через эту точку начинает работать второе уравнение. Характер фазовой линии такой, что она постоянно приближается к началу координат, т.е. нелинейная система с релейным элементом устойчива. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается, а частота переключения растет. Получаем, что амплитуда колебаний в итоге примет нулевое значение, а частота колебаний станет бесконечно большой.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1 Основы автоматического регулирования/Под ред. В.С. Пугачева. – М.: Наука, 1974. – 720 с.: ил.
2 Теория автоматического управления/Под ред. А. В. Нетушила.– М.: Высшая школа, 1976. – 400 с.: ил.
3 Основы теории автоматического регулирования/А.А. Воронов и др. – М.: Высшая школа, 1977. – 519 с.: ил.
4 Автоматические приборы и регуляторы/ Кошарский Б.Д., Бек В.А., и др. – М.: Машиностроение, 1964. – 704 с.: ил.
5 Автоматизация производства и промышленная электроника/Берг А.И., Трапезников В.А. – М.: Советская энциклопедия, 1962. – 544 с.: ил.
