Найдем критерии устойчивости замкнутой системы по критериям Найквиста.

Критерий Найквиста дает возможность судить об устойчивости замкнутой системы посредством исследования разомкнутой. Руководствуясь формой и расположен на комплексной плоскости амплитудно-фазовой характеристики разомкнутой системы, можно судить о динамических свойствах замкнутой системы.

– частотная функция разомкнутой системы

Re W(=

Годограф строится на комплексной плоскости, т.е. вещественная часть откладывается по оси абсцисс, а мнимая по оси ординат – рис. 8.

Значения вещественной и мнимой части при различных частотах приведены в таблице 3.

Согласно критерию устойчивости Найквиста, для того чтобы замкнутая система регулирования была устойчива, нужно, чтобы соблюдалось условие:

А

мплитудно-фазовая характеристика системы, полученная при изменении частотыω от -∞ до +∞ , не должна охватывать точку (-1; jo).⁴

Рисунок – 8 Годограф Найквиста

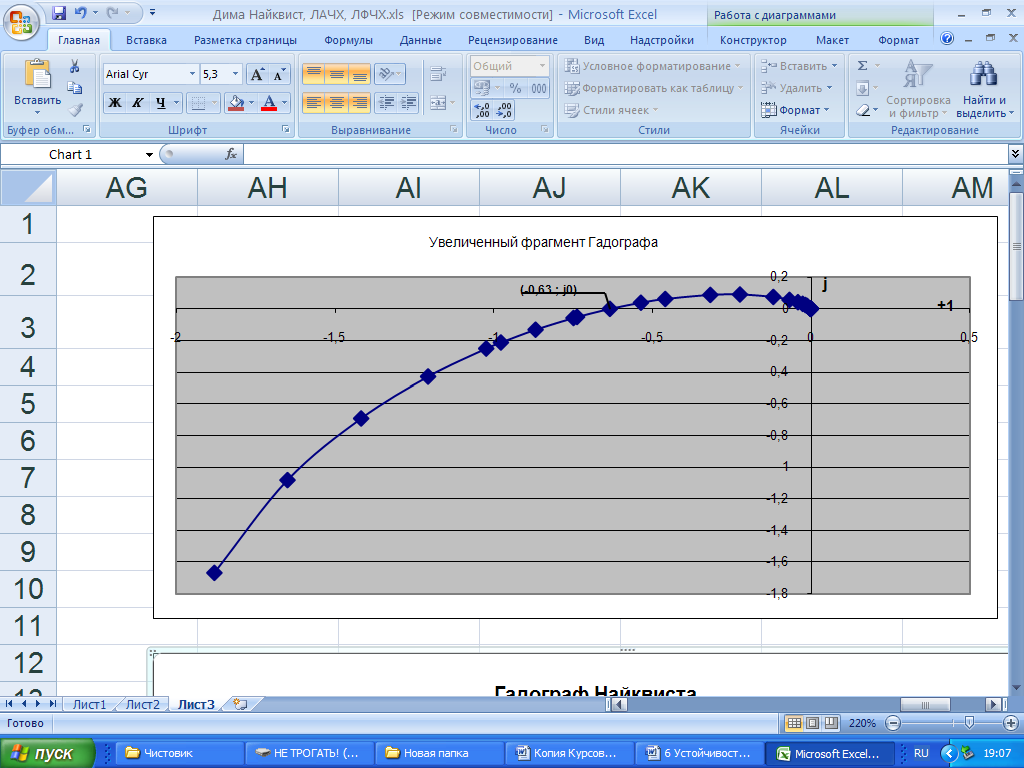
Рисунок – 9 Увеличенный фрагмент годографа Найквиста

Из увеличенного фрагмента годографа Найквиста рис. 9 видно, что годограф исследуемой системы не охватывает точку (-1; jo), следовательно, согласно критерию Найквиста система устойчива.

6. Логарифмические частотные характеристики разомкнутой сау, запасы устойчивости по амплитуде и фазе.

В

ыражениеназывают комплексной частотной функцией разомкнутой системы. Эту функцию можно представить в декартовых координатах на комплексной плоскости как комплексную суммуиили же её можно также представить в полярных координатах в показательной форме с модулеми фазой.

A()

Где А()= Q()=arctg

Величина A( - определяет измерение амплитуды

Величина Q( -) определяет измерение фазы колебания

Тогда ЛАЧХ будет иметь вид L(=20 lg A(

L(=20 lg

ЛАЧХ – характеристика построена в логарифмическом масштабе

ЛФЧХ – характеристика построена в логарифмическом масштабе и в обычном масштабе для фазы по оси ординат

ЛФЧХ имеет вид Q()=arctg

Построение асимптотическую логарифмическую частотную характеристику

Рисунок - 10. Схема системы управления

1. - асимптотическое звено. Асимптотическую логарифмическую частотную характеристику можно представить в виде двух отрезков прямых. Первый параллельный оси обцисе и расположении на расстоянии 20дб/дек. Эти отрезки сопрягаются при

ωт==2,3256

Частота ωт называется сопрягающей

2. – колебательное звено.

Асимптотическая ЛАХ можно представить в виде двух отрезков прямых. Первые параллельные оси обцисе и расположении на расстоянии 20 lg 0,46. Второй имеет наклон минус 40 дб/дек. Эти отрезки сопрягаются при

⇒

- безинертное звено. Асимптотическая ЛАХ можно представить собой прямую параллельна оси обцисе и проходит на расстоянии 20 lg от оси.

20 lg = 20 lg =18,06

20 lg = 20 lg = 13,98

20 lg 0,46 = -6,74

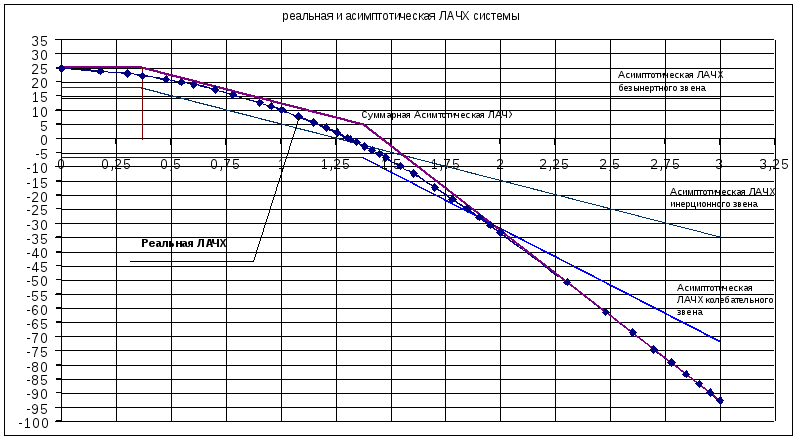
Рисунок – 11 Реальная ЛАЧХ

Построение асимптотическую фазно-частотную характеристику

Рисунок - 10. Схема системы управления

1. – безинертное звено. Его асимптотическая фазно-частотная характеристика показывает отсутствие фазного сдвига – прямая принадлежит оси обцисе.

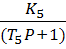2. - колебательное звено. Его асимптотическая фазно частотная характеристика представляет собой кривая графика определяется по формуле

Q()=arctg(*)

3. - колебательное звено.

Приближенная фазовая характеристика может быть по следующей формуле

Q()=arctg=- arctg

общий вид колебательного звена

=

Рисунок – 12 Асимптотическая ЛФЧХ