3. Передаточные функции замкнутой сау

Рисунок – 5 Схема разомкнутой системы

Передаточная функция разомкнутой системы имеет вид:

А. Передаточная функция замкнутой системы:

Б. Передаточная функция по ошибки:

В. Передаточная функция по возмущению.

4. Область устойчивости замкнутой системы, построенная методом d-разбиения по неизвестному коэффициенту усиления.

В том случае, когда требуется выяснить влияние на устойчивость только одного параметра при заданных значениях остальных параметров, целесообразно ввести вместо этого параметра ввести комплексную величину, вещественная часть которой равна исследуемому параметру.

Построим область устойчивости по коэффициенту ;

Найдем, максимальное значение разомкнутой системы при которомзамкнутая система теряет устойчивость. Характеристический полином системы приводят к следующему виду

Запишем характеристическое уравнение замкнутой системы

В том случае когда требуется выяснить влияние на устойчивость только одного параметра при заданных остальных, целесообразно ввести вместо этого параметра комплексную величину Р=jω

Вещественная часть Х()=

Мнимая часть У()=

При Х()= У()= следовательно годограф проходит через точку (-0,2625;0)

Найдем точки перехода комплекса К() с отдельными координатами

1. У(=0

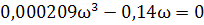
Тогда Х()=0,0121*669,85-0,2625=7,842

2. Х(=0

1,21

Тогда У(=0,000209*101,028-0,14*4,657=-0,63

При У(= ±0,63

Построим кривую годографа.

Таким образом область устойчивости является отрезок вещественной оси заключенный между точками с координатами [-0,2625; jω) и [7,842; j0)

Следовательно граничное значение коэффициент передачи разомкнутой системы К*=7,842

Рисунок – 6 Годограф АФЧХ

2.4 Оценка устойчивость разомкнутой сау по критерию Гурвица.

Наиболее распространенная в технической практике форма алгебраического критерия устойчивости известна под названием критерия Гурвица. Этот критерий формулирует условия устойчивости в форме определителей.

Передаточная функция разомкнутой системы имеет вид:

Характеристика полином замкнутой системы

Д

ля системы третьего порядка , необходимо и достаточно , чтобы все коэффициенты характеристического уравнения были положительны и чтобы определитель второго порядка был положителен.

Условие устойчивости: 1)

2)

Составим определитель 3-го порядка из коэффициентов

⇒ 0,0077

0,0077(9,66+*36,8<2,308

0,0743+0,283<2,308

Поскольку первое условие устойчивости выполняется, то система будет устойчива при

0<<7,89

5. Исследование устойчивости замкнутой сау по критериям Михайлова и Найквиста.

Критерий устойчивости Михайлова позволяет судить об устойчивости системы по виду её частотной характеристики. Критерий устойчивости Михайлова предполагает построение характеристического годографа системы D(jω)

(где коэффициент К₁=5 взят из области устойчивости, найденной методом D разбиения, и исследованием устойчивости системы по критерию Гурвица.)

Характеристический полином замкнутой системы имеет вид

Произведем замену Р=jω

+

+

Выделяем вещественную и мнимую части

Вещественная часть - ReД(=

Мнимая часть -

Кривая годографа строится в комплексной плоскости - рис. 7.

Рисунок – 7 Кривая Михайлова

Кривая годографа строится в комплексной плоскости, т.е. По оси абсцисс откладывается вещественная часть, по оси ординат мнимая часть рисунок 7. Значения вещественной и мнимой части при различных частотах приведены в таблице 2.

С

огласно критерию Михайлова, для устойчивости системыn порядка необходимо и достаточно, чтобы годограф Михайлова при изменении частоты ω от 0 до +∞ начинался на вещественной положительной полуоси и последовательно обходил n квадрантов комплексной плоскости в направлении против часовой стрелки.

Исследуемая в этой курсовой работе система управления - система третьего порядка. Годограф исследуемой системы при изменении частоты ω от 0 до +∞ начинается на вещественной положительной полуоси, в точке (193,66 ; 0) и последовательно обходит 3 квадранта комплексной плоскости в направлении против часовой стрелки.

Годограф располагается на комплексной плоскости. Годограф устойчив системы n-го порядка, кривая проходит без пропусков последовательно n квадратов справа на лево. Данное условие выполняется ⇒ система устойчива.

Условие устойчивости выполняются, следовательно, согласно критерию Михайлова система устойчива!