4. Структурное упрощение сау.

1 этап: перенос сумматора через звено W₁ по ходу сигнала.

2 этап: параллельное соединение звеньев.

3 этап: перенос сумматора через звено W₃· K_пi ·W₂.

4 Этап: перенос узла через звено w7 против хода сигнала. Параллельное соединение звеньев.

5 этап: Встречно параллельное соединение звеньев W₇, W₈, W₉.

6 этап: получение конечной передаточной функции по каналу напряжению

Характеристическое уравнение системы имеет вид:

где

5. Исследование устойчивости сау

Основной динамической характеристикой автоматической системы является ее устойчивость. Устойчивостью называют способность системы возвращаться в исходное состояние равновесия (асимптотическая устойчивость) или переходить в новое установившееся состояние (нейтральная устойчивость) после исчезновения внешнего воздействия (возмущающего или управляющего).

В зависимости от переходного процесса системы различают три основных случая поведения системы после возмущающего воздействия.

1. Система не может восстановить равновесного состояния, значение управляемой переменной все больше отклоняется от заданного; такой процесс называется расходящимся, а система – неустойчивой;

2. Система возвращается к равновесному состоянию, значение управляемой переменной отличается от заданного на величину статической погрешности системы; такой переходный процесс будет сходящимся, а система – устойчивой;

3. Система характеризуется установившимся периодическим движением; такой процесс называется незатухающим колебательным, а система будет находиться на границе асимптотической устойчивости.

Первая теорема А.М.Ляпунова:

Если корни характеристического уравнения системы отрицательные, то движение в системе устойчиво асимптотически. В противном случае могут иметь место частные варианты.

Вторая теорема А.М.Ляпунова:

Если в характеристическом уравнении имеются особые корни (равные нулю или бесконечности, мнимые), то система может оказаться на границе устойчивости и для окончательного суждения необходимо учитывать нелинейность.

Таким образом анализ устойчивости требует решения корней характеристического уравнения.

1. 1+W_раз(р)=0

2. N(p)+M(p)=0

1. Критерий Михайлова.

Система будет устойчива, если при 0≤ω≤∞ вектор A(jω)=1+W(jω), начав движение от вещественной оси комплексной плоскости, вращаясь против часовой плоскости и нигде не обращаясь в ноль, обходит последовательно n квадрантов (где n – степень характеристического уравнения).

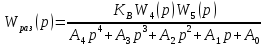
Осуществим замену p=jω:

Изменяя частоту ω=0÷500, получим годограф Михайлова.

Рис.14. Годограф Михайлова на комплексной плоскости.

Из графика видно, что функция В(ω) проходит последовательно через все четыре квадранта против часовой стрелки, следовательно, система устойчива.

2. Критерий Найквиста.

Критерий Найквиста позволяет судить об устойчивости замкнутой САУ по форме амплитудно-фазовой характеристики (АФХ) разомкнутой САУ с единичной обратной связью.

Если система устойчива в разомкнутом состоянии, то для устойчивости соответствующей замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы для 0≤ω≤∞ не охватывала точку с координатами (-1, j0). Только в этом случае приращение аргумента вектора F(jω) будет равно нулю.

АФХ разомкнутой системы:

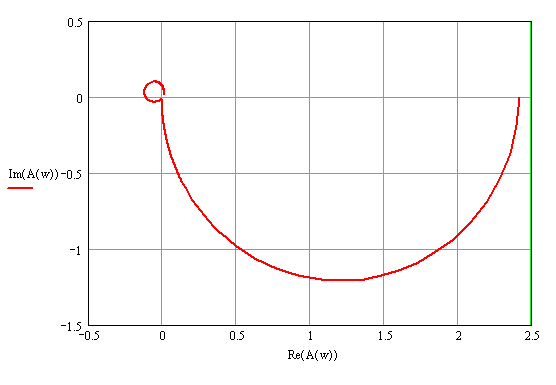
Рис. 15.Критерий Найквиста на комплексной плоскости.

Как видно из графика, A(ω) не охватывает точку [-1;0], следовательно, система устойчива.