Лекция №21

АНАЛИЗ ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ.

План лекции:

1.Понятия свободного и вынужденного движения в импульсной системе.

2. Аналитическое выражение для вынужденного движения.

3. Анализ точности при полиномиальных (степенных) воздействиях.

4. Коэффициенты ошибок дискретной системы.

21.1.Свободный и вынужденный процессы в импульсных системах.

Точность воспроизведения входных воздействий является одной из наиболее важных характеристик импульсных систем. При исследовании точности автоматических систем обычно рассматривают вынужденные процессы, то есть процессы устанавливающиеся по истечении бесконечно большого промежутка времени после подачи входного воздействия. Рассмотрим, как определяются вынужденные процессы в импульсных системах.

Реакция импульсной системы (безразлично, замкнутой или разомкнутой) на входное воздействие f[kT] определяется соотношением:

, (21.1)

где w[kT] - импульсная переходная функция системы, связанная с ее z- передаточной функцией зависимостью:

w[kT]=Z^-1{w(z)}.

Формула (21.1) записана в предположении, что входное воздействие приложено в момент времени k=0. Если же входное воздействие приложено в произвольный момент времени k=k₀, то выражение (21.1) примет вид:

.

Пусть , то есть между моментом приложения входного воздействия и моментом наблюдения прошло бесконечно большое время. Такой процесс в системе мы назовем вынужденным и обозначим его черезx_в[kT]. Тогда:

. (21.2)

Проведем замену переменных по формуле k-i=j. Тогда выражение (21.2) трансформируется в следующее выражение для вынужденного процесса:

. (21.3)

Разность между общим процессом (21.1) и вынужденным процессом (21.3) определяет свободный процесс импульсной системы x_c[kT]:

x_c[kT]=x[kT]-x_в[kT],

или, с учетом (21.1) и (21.3):

.

Таким образом, свободный процесс определяет отклонение общего процесса в импульсной системе от вынужденного.

Вернемся к формуле (21.3). Разложим входное воздействие в ряд Тейлора по переменной j в окрестности точки kT:

, (21.4)

где .

Подставив выражение (21.4) в формулу (21.7), получим:

.

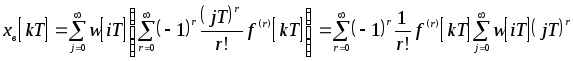Обозначим: и назовем эту величину моментом второго порядка весовой характеристикиw[kT].

Тогда выражение для вынужденного процесса в системе приобретает вид:

. (21.5)

Числа d₀, d₁, ... характеризуют дискретную систему и могут быть вычислены заранее. Производные также легко определяются (особенно это просто делается для степенных входных воздействий) и, таким образом, зависимость (21.5) позволяет построить вынужденные процессы в системе.

Для определения моментов d₀, d₁, ... можно использовать следующую формулу:

, гдеW^*(p) - передаточная функция импульсной системы, соответствующая дискретному преобразованию Лапласа:

Указанная зависимость получается r- кратным дифференцированием формулы D- преобразования функции w[kT] :

с последующей подстановкойp=0 .

Протекание переходных процессов в ИС имеет свои особенности. В частности, здесь оказываются возможными процессы, затухающие за конечное время, так называемые процессы конечной длительности. Определим условия их возникновения в дискретной системе с передаточной функцией W(z). Рассмотрим импульсную передаточную функцию w[kT] и установим, когда возможно выполнение равенства:

w[kT]=0, k>k₀ . (21.6).

Пусть передаточная функция W(z) является дробно-рациональным выражением, то есть:

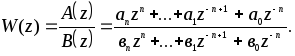
Функции w[kT] и W(z) связаны между собой z- преобразованием, то есть с учетом равенства (21.6):

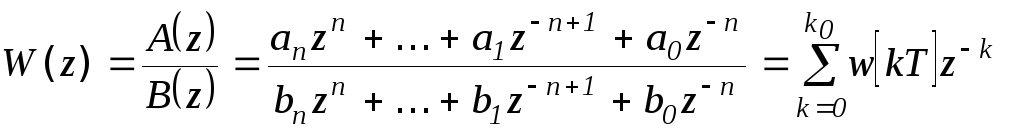. (21.7)

Очевидно, что равенство (21.7) возможно при выполнении условий:

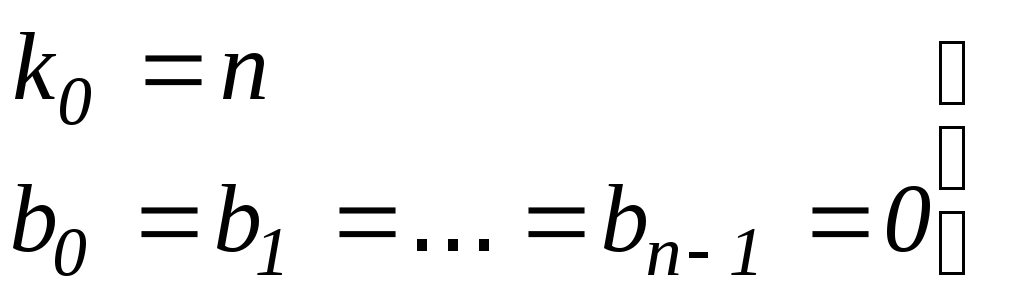. (21.8)

Таким образом, выполнение условий (21.8) влечет за собой выполнение равенства (21.6). С учетом равенства (21.6) при k₀=n из выражения (21.1) имеем:

x_c[kT]=0, k=n,n+1...,

то есть свободные процессы в системе заканчиваются за n- шагов квантования, где n- порядок системы.

После этого в системе устанавливается вынужденный процесс x_в[kT]. Наличие процессов с конечной длительностью, то есть выполнение условий (21.8), обеспечивается надлежащим выбором параметров исходной системы или параметров дополнительного корректирующего устройства. Отметим, что характеристическое уравнение такой системы имеет вид:

в_nzⁿ=0,

то есть устойчивость такой системы гарантируется.