ЛЕКЦИЯ № 23

ИМПУЛЬСНАЯ КОРРЕКЦИЯ ДИСКРЕТНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ

План лекции:

1. Общие сведения об импульсной коррекции дискретных систем.

2. Определение передаточной функции корректирующего устройства.

23.1 Общие сведения об импульсной коррекции дискретных систем.

В предыдущей лекции отмечалось, что реализация желаемых ЧХ дискретной системы с помощью непрерывного фильтра имеет ряд существенных недостатков

От этих недостатков свободен способ импульсной коррекции, к рассмотрению которого мы переходим

При реализации импульсного способа коррекции в систему вводится дискретный фильтр, преобразующий последовательность дискретных входных величин в выходную последовательность импульсов, то есть функциональная схема этого устройства имеет вид, приведенный на рис.23.1.

Рис.23.1.

Структурную схему импульсной системы с последовательно – включенным дискретным КУ можно представить в виде (рис.23.2):

Рис.23.2.

Здесь - передаточная функция приведенной непрерывной части ДКУ;

- передаточная функция приведенной непрерывной части объекта управления

Таким образом, из предыдущей схемы следует, что - передаточная функция разомкнутой скорректированной системы определяется выражением:

,

где - передаточные функции ДКУ и объекта управления соответственно, те

;

23.2 Определение передаточной функции КУ.

Определение ПФ ДКУ осуществляется по желаемой - ПФ разомкнутой системы с учетом места установки ДКУ в контуре управления

Так, структурная схема ИС с последовательной коррекцией представлена на рис.23.3.

Рис.23.3.

Здесь - ПФ приведенной НЧ дискретного фильтра, - ПФ приведенной НЧ исходной системы. Тогда для определения Z – ПФ ДКУ легко получить зависимость

. (23.1)

В выражении (23.1) - желаемая ПФ системы, соответствующая желаемым ЛАФЧХ , Z – ПФ исходной системы (располагаемая Z – ПФ) Соотношение (23.1) может быть сразу записано и для ЧХ в виде:

Включение ДКУ при параллельной коррекции показано на рис.23.4.

Р ис.23.4.

Структурные преобразования показаны на рис.23.5.

Р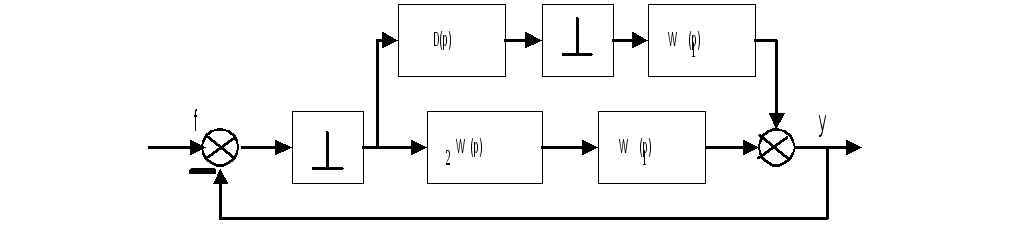 ис.23.5.

Здесь ПФ приведенной НЧ исходной системы определяется ПФ произведением  Тогда определяя ПФ разомкнутой системы и приравнивая ее к желаемой Z – ПФ , получим:

где ;

Тогда ПФ дискретного фильтра определится зависимостью:

(23.2)

Возможны и другие варианты включения ДКУ в контур управления Они рассмотрены в ряде учебников

При определении - ПФ дискретных фильтров следует обязательно проверять условия их физической реализуемости, то есть степень числителя не должна превосходить степень знаменателя

При импульсной коррекции особенно удобно использовать метод ЛАПЧХ При этом частотные характеристики КУ определяются графически точно также, как и при синтезе непрерывных КУ

тк , поделим числитель и знаменатель на , получим

Отсюда хорошо видна сущность условия физической реализуемости

И так, повторим шаги, которые необходимо выполнить при синтезе дискретных систем.

1. Находим ПФ располагаемой приведенной непрерывной части без коррекции:

.

2. Используя билинейное преобразование, переходим к новой переменной:

,

то есть определяем .

3. Переходим к псевдочастоте в результате замены .

4. Строим располагаемые ЛАФПЧХ:

5. Исходя из требуемой точности определяем запретную область (рис.22.2).

6. Определяем псевдочастотную передаточную функцию корректирующего звена.

7. Переходим к эквивалентному конечно-разностному уравнению, реализующему синтезированный корректирующий фильтр.

23.3 Некоторые вопросы реализации импульсных фильтров.

При синтезе ИС мы можем определить - ПФ дискретного фильтра Она определяется, например, из формул (23.1) и (23.2) или после нахождения ЛАФЧХ фильтра  Пусть передаточная функция является дробно-рациональной функцией, те

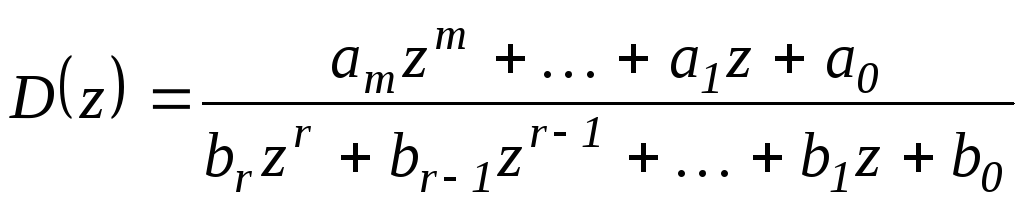(23.3)

где  По ПФ (23.3) легко составить разностное уравнение фильтра:

,

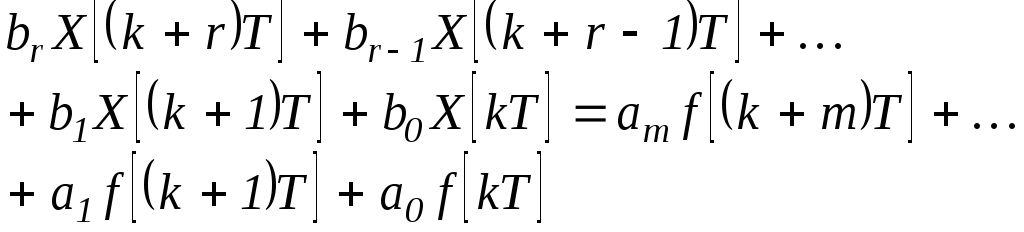(23.4)

где и - соответственно входная и выходная переменные дискретного фильтра

Реализацию ИФ можно осуществить двумя основными способами

Первый способ состоит в том, что подбирается приведенная непрерывная часть фильтра, обеспечивающая получение необходимой - ПФ. При втором способе выполняется непосредственное решение разностного уравнения (7.8) с помощью ЦВМ

Рассмотрим первый способ

При определении ПФ приведенной непрерывной части по известной - ПФ можно воспользоваться обратным - преобразованием , те:

Недостаток этого подхода заключается в том, что определяемая таким способом ПФ может оказаться слишком сложной Поэтому имеются специальные способы реализации ИФ с помощью непрерывных элементов В частности, отметим один из способов, заключающийся в построении системы, состоящей из элементов задержки и суммирующих усилителей При этом из указанных элементов составляется схема моделирования, аналогичная тому, как это делалось ранее при выборе переменных состояния системы При составлении схемы могут применяться способы прямого, параллельного и последовательного программирования

Вторым часто используемым способом реализации импульсного фильтра является решение разностного уравнения (23.4) с помощью ЦВУ (цифрового фильтра) В этом случае непрерывный сигнал подвергается аналого–цифровому преобразованию (АЦП), те переводится в цифровой код, а решение , получаемое в ЦВУ в реальном масштабе времени вводится в непрерывную часть системы через ЦАП Алгоритм работы цифрового вычислительного устройства представлен на рисунке 23.6.

Реализация данного способа коррекции предполагает последовательное выполнение операций квантования по уровню и по времени, решение разностного уравнения в ЦВУ и формирование непрерывного сигнала из дискретного с помощью экстраполятора нулевого порядка Второй ИЭ вводится для того, чтобы учесть дискретный по времени характер выдачи информации

При условии в формуле (23.4) значение определяется предыдущими значениями входного сигнала 



Чтобы сохранить в ЦВУ эти предыдущие значения, его быстродействие должно быть таким, чтобы за время, не превышающее Т, выполнить все необходимые расчеты При быстродействие ЦВУ должно обеспечивать проведение расчетов за время, пренебрежимо малое в сравнении с интервалом квантования или же необходимо учитывать запаздывание, вносимое ЦВУ

Рис.23.6.

Если число разрядов АЦП достаточно велико, то нелинейностью, вносимой квантованием по уровню, можно пренебречь Тогда получится обычная схема импульсного фильтра, представленная на рис.23.7.

Рис.23.7.

РАССМОТРИМ ПРИМЕР

Рассмотрим пример синтеза дискретного корректирующего устройства, включаемого последовательно с неизменяемой частью системы Передаточная функция приведенной непрерывной части исходной системы имеет вид:

,

где



Желаемая ЛАЧХ () системы представлена на рис.23.8. 

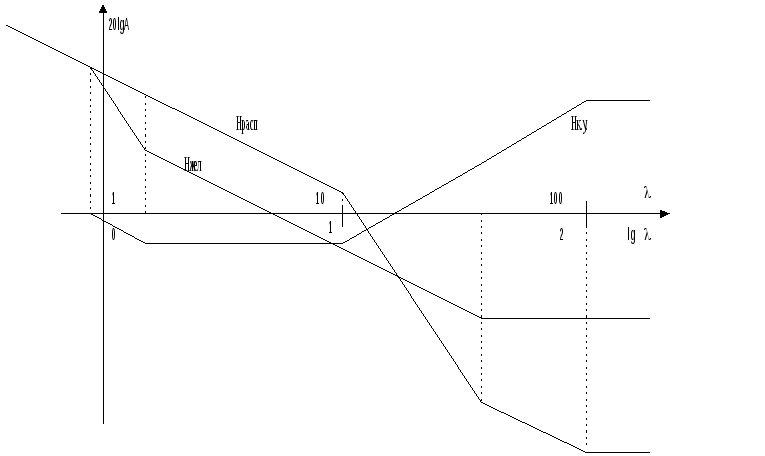
Рис.23.8.

Найдем располагаемую ЛАЧХ импульсной системы, для чего по передаточной функции:

определим - передаточную функцию 

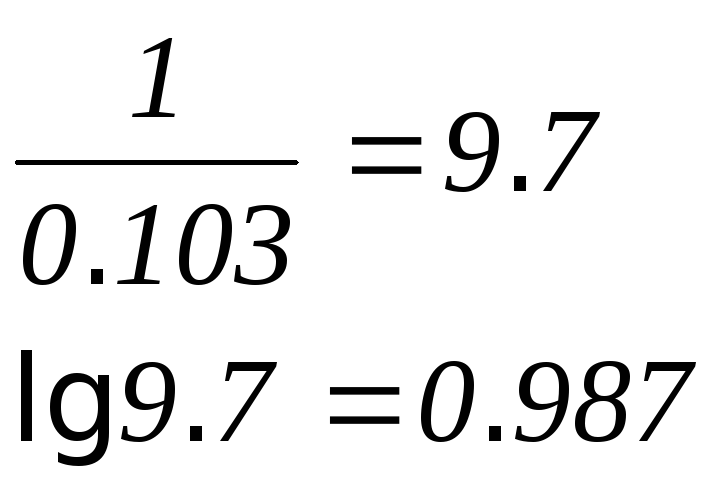
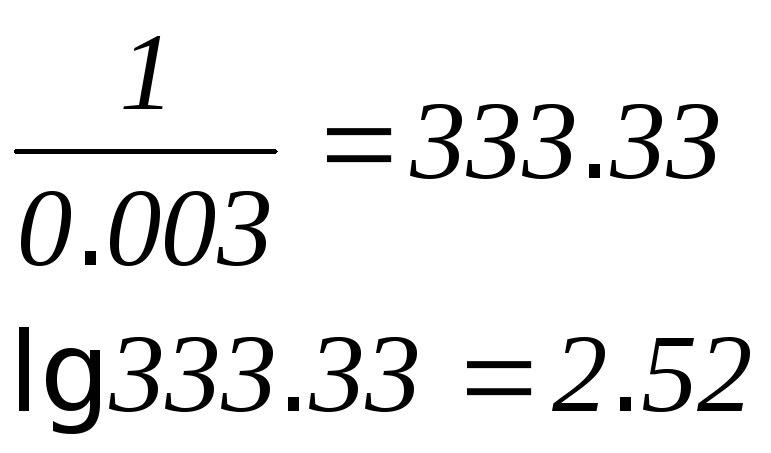
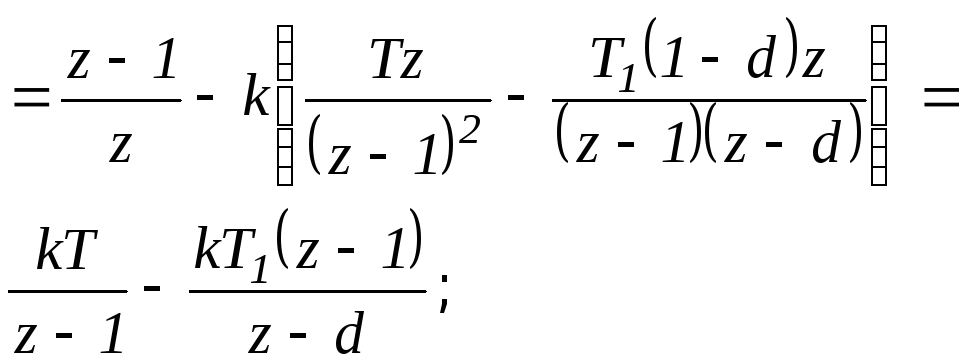
Подставляем , получим:

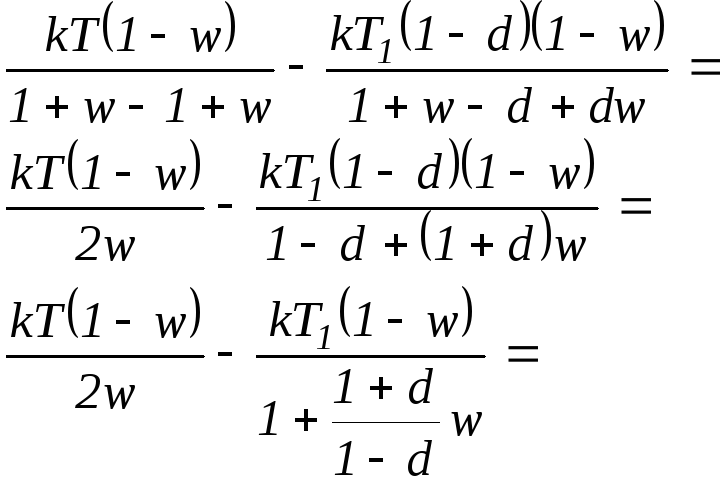
Введем обозначение : .

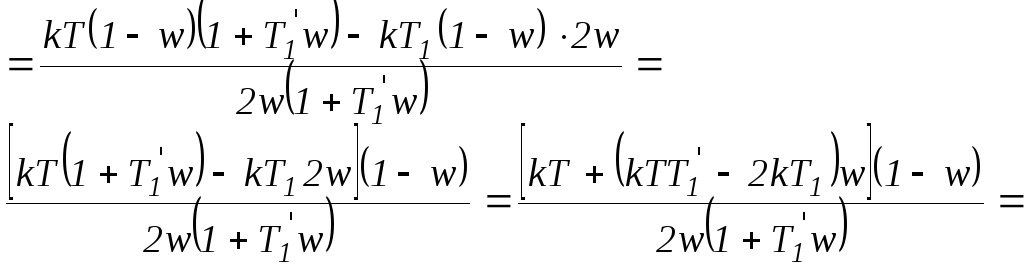
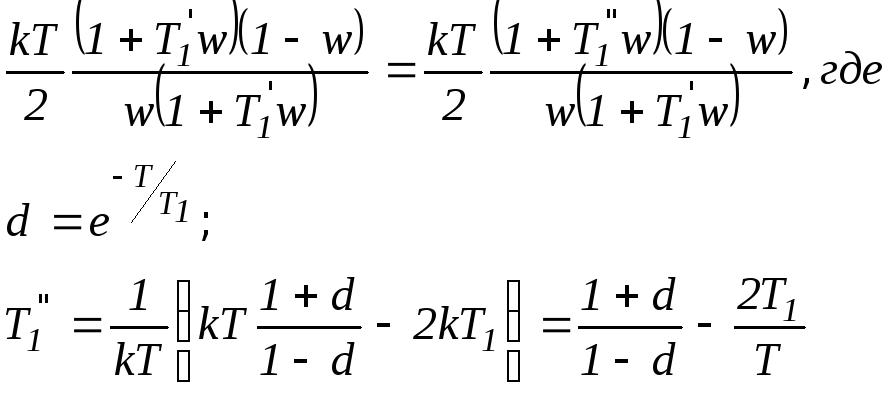
Далее вместо выполним замену: .

в числах:

Располагаемая ЛАЧХ представлена на рис.7.12.:

Тогда - передаточная функция коррекционного устройства имеет вид:

или

Переходим с помощью билинейного преобразования к переменной Z:

Получим:

.

Рассмотрим пример реализации данного дискретного фильтра ЦВУ.

Схема моделирования фильтра методом прямого программирования:

Запишем ПФ КУ в общем виде:

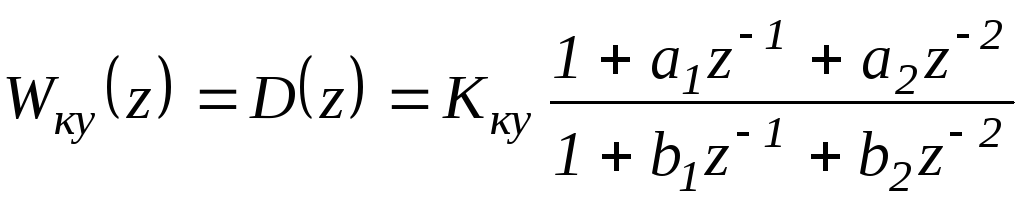
Введем в промежуточную функцию :

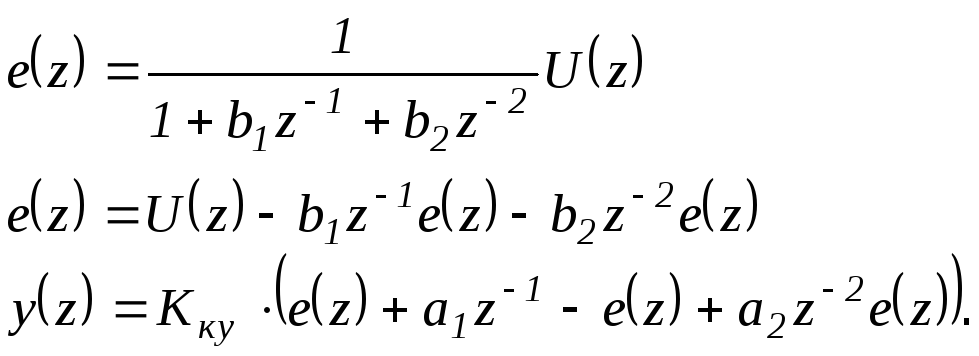
Структурная схема приведена на рис.23.8.:

e(z) x(z) x1(z) S y(z)

Рис.23.8.

Обозначим переменные:

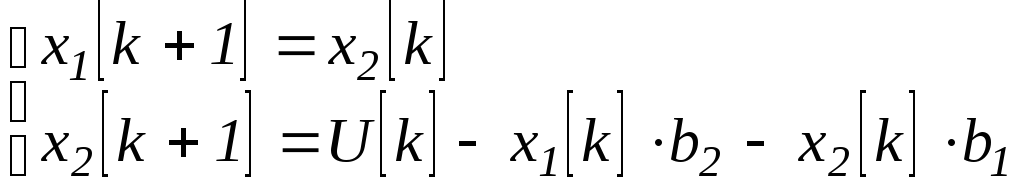
155