лекции / lekcii_kompyuternoe_upravlenie / КУ_Л_20

ЛЕКЦИЯ № 20

УСЛОВИЕ УПРАВЛЯЕМОСТИ И НАБЛЮДАЕМОСТИ

ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ.

План лекции:

1. Определение полностью управляемой системы.

2. Условие управляемости линейной импульсной системы.

3. Определение наблюдаемости и восстанавливаемости.

4. Условие восстанавливаемости линейной импульсной системы.

Управляемость системы определяет возможность управления со стороны входа всеми компонентами вектора состояния дискретной системы.

Система, процесс или объект называются полностью управляемыми, если они могут быть переведены из состояния x[0]=0 в произвольное состояние x[n] с помощью управления за конечное число шагов.

Рассмотрим систему разностных уравнений:

x[k+1]=Фx[k]+Hu[k]

y[k]=cx[k]+Du[k] (20.1),

где x=(x₁,...x_n)- вектор состояния;

y=(y₁,...y_n)- вектор входных переменных;

u=(u₁,...u_n)- вектор управления.

Предположим, что последовательность управлений имеет вид:

u[0],u[1],...u[n-1] . (20.2)

Тогда в соответствии с (5.44) при x[0]=0, получим:

x[1]=Hu[0];

x[2]=ФHu[0]+Hu[1];

x[3]= Ф²Hu[0]+ Ф Hu[1];

. (20.3)

Найдем последовательность управлений (20.2), переводящую точку x[0]=0 в точку x[u]=x. Последнее уравнение системы (20.3) также можно представить в виде:

. (20.4)

Это выражение можно рассматривать как систему линейных алгебраических уравнений относительно компонентов векторов

u[n-1], u[n-2] ,..., u[0].

Каждый вектор u имеет m скалярных компонент, так что число неизвестных равно m x n . Основная матрица системы

-

- имеет размерность (n x mn), а расширенная матрица

-

- размерность (пхтп+1).

Рассмотрим условие управляемости, то есть условие существования решения (20.4).

Для существования решения системы (20.4), как известно, необходимо и достаточно, чтобы совпадали ранги основной и расширенной матриц.

Легко видеть, что так как , то . Если ранг основной матрицы меньше порядка системы п, то всегда можно так подобрать вектор Х, что ранг расширенной матрицы станет больше ранга основной матрицы.

Таким образом, чтобы система уравнений (20.4) имела решение при произвольном Х необходимо и достаточно, чтобы .Это условие полной управляемости линейной дискретной системы.

Рассмотрим случай скалярного управления и перейдем в исходной системе (5.44) с помощью преобразования

к каноническим переменным:

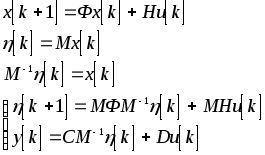
Окончательно получим:

,

где

Существуют специальные алгоритмы приведения исходной матрицы Ф к каноническому виду (диагональной форме).

Структурная схема системы приведена на рис.20.1 (при условии скалярного выхода y).

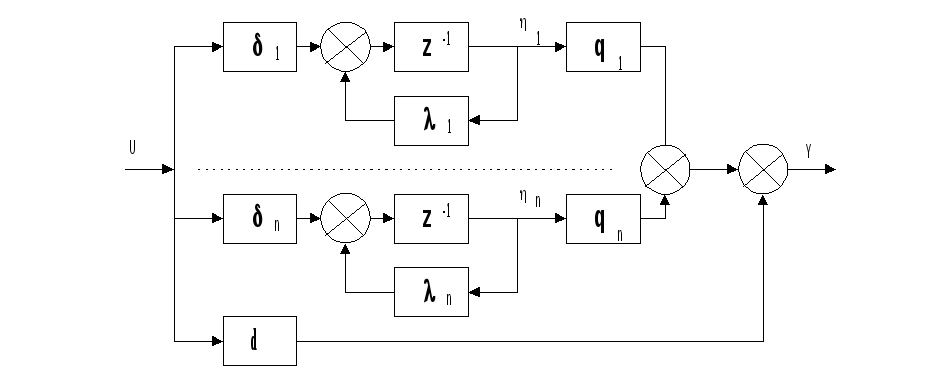
Рис.20.1.

Легко видеть, что по свойствам полной управляемости системы соответствует отсутствие нулей у вектора , то есть условия .

Наиболее распространенным алгоритмом управления систем, синтезируемых с помощью МПС, является алгоритм

.

Однако, во многих случаях состояние системы

не измеряется, и, следовательно, управление согласно вышеприведенному соотношению не может быть непосредственно реализовано.

Таким образом, возникает вопрос, можно ли определить вектор состояния по измеряемому выходу или по измеряемым выходам объекта со многими входами и многими выходами.

В этой связи в теории управления различают наблюдаемость состояния и восстанавливаемость состояния.

Состояние х(t_o) системы наблюдаемо, если оно может быть определено по будущим значениям выходной переменной y(t), t>t₀ и если интервал t-t₀ конечен.

Состояние х(t_o) системы восстанавливаемо, если оно может быть определено по прошлым значениям выходной переменной y(t), t>t₀ и если интервал t-t₀ конечен.

Условие наблюдаемости и восстанавливаемости можно получить из уравнения выхода системы:

и уравнения состояния:

.

Вычисляя последовательно значения выходной переменной для моментов времени k,k+1,...k+n-1, получим:

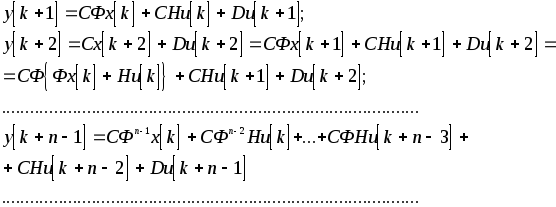(20.5)

или в векторно-матричной форме:

или в компактной форме:

Y_n[k]=Q_px[k]+P_pu[k].

Если матрица Q_p невырожденная, то существует ее обратная матрица Q^-1_P , в этом случае detQ_p и строки матрицы Q_p линейно независимы.

Тогда из предыдущего матричного уравнения следует:

x[k]=Q^-1_py_n[k]- Q^-1_pP_p u[k] (20.6)

Таким образом, мы можем сформулировать следующее условие наблюдаемости: линейная система, описываемая КРУ, наблюдаема, если и только если ранг матрицы Q_p равен размерности n пространства состояний.

Получим условие восстанавливаемости:

Учитывая, что x[k+n]=Фⁿx[k], то последнее матричное уравнение может быть преобразовано к виду:

, где .

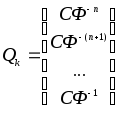Условия восстанавливаемости формулируются аналогично условиям наблюдаемости: линейная система, описываемая системой КРУ, восстанавливаема, если и только если ранг матрицы Q_p равен размерности n пространства состояний.

Понятие управляемости, наблюдаемости и восстанавливаемости позволяет лучше представлять особенности динамики исследуемой системы, ее возможности. Отметим, что матрица Ф зависит от величины интервала квантования Т, поэтому свойства управляемости и наблюдаемости могут изменяться при переходе от непрерывных систем к цифровым (вспомним, например, о возможности возникновения скрытых колебаний в дискретных системах).

Таким образом, мы завершаем рассмотрение вопросов анализа динамики дискретных систем в рамках методов ПС. В настоящее время этот метод широко применяется в инженерной практике. Его развитию будет способствовать все более широкое использование ЭВМ в проектировании рассматриваемых систем, так как именно он позволяет в наибольшей степени соединить полноту и строгость теоретического исследования с возможностями современной вычислительной техники.

129