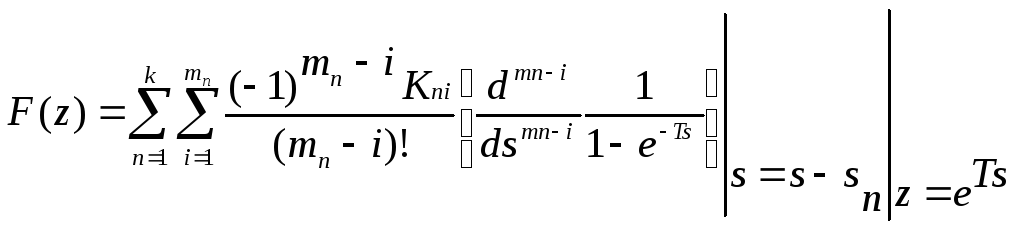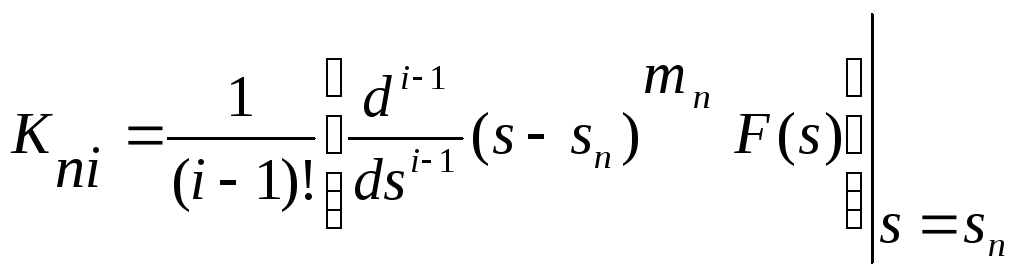лекции / Лекции дсау / ДСАУ 3_2

3. Дискретные преобразования и их основные свойства.

Z-преобразование_____________________________________________________________

3.2. z-Преобразование

3.2.1. Определение z-преобразования

z-Преобразование является одним из математических методов, разработанных для анализа и проектирования дискретных систем. Аппарат z-преобразования играет для цифровых систем ту же роль, что и преобразование Лапласа для непрерывных систем.

Недостатком дискретного преобразования Лапласа является трансцендентность его аргумента e^q. Действительно, рассмотрим преобразование Лапласа квантованного сигнала:

 

L{f*(t)}= F*(s) = Σ e^-nTs f[nT] или D{f*[n]} = F*(q) = Σ e^-qn f[n]. ( 1 )

n=0 n=0

Как было показано в предыдущем разделе 3.1, выражение F*(q) не является рациональной функции относительно аргумента q, поскольку оно содержит множитель e^-qn, не свойственный большинству передаточных функций непрерывных систем. Когда в передаточной функции появляется множитель e^-qn, могут возникнуть трудности при вычислении обратного преобразования Лапласа. Следовательно, желательно сначала преобразовать иррациональную функцию F*(s) (или функцию F*(q)) в рациональную, обозначаемую F(z). Такое преобразование выполняется с помощью замены комплексной переменной:

z = e^sT или z = e^q ( 2 )

Решая уравнение (2) относительно s, получим

s = 1/T ln z. ( 3 )

В последних выражениях T – период квантования; z – комплексная переменная, действительная и мнимая части которой определяются как

Re z = e^TσcosωT, ( 4 )

Im z = e^TσsinωT, ( 5 )

где s = σ + jω. ( 6 )

Связь между s и z может быть определена как z-отображение. Подставляя (2) в (1), получим:



F*[s = 1/T ln z] = F(z) = Σ f[nT] e^-n . ( 7 )

n=0

Таким образом, F(z) можно определить как z-преобразование функции f(t), т.е.

F(z) = Z{f(t)}.

Поскольку z-преобразование f(t) получается из преобразования Лапласа для функции f*(t) заменой z = e^Ts, то в общем случае для любой функции f(t), имеющей преобразование Лапласа, существует также и z-преобразование.

Процедура нахождения z-преобразования непрерывной функции содержит следующие три этапа:

1. определение f*(t) как выходного сигнала идеального квантователя для входной функции f(t);

2. определение преобразования Лапласа для функции f*(t)



F*(s) = L{f*(t)} = Σ f[nT] e^-nTs .

n=0

3) замена e^Ts на z в выражении для F*(s), чтобы получить



F*(s) = L{f*(t)} = Σ f[nT] z^-n . ( 8 ) n=0

Выражение (8) используется для нахождения z-преобразования функции f(t). Однако неудобство этого выражения состоит в том, что оно является бесконечным рядом, а не эквивалентной функцией в компактной форме.

Если функцию F(s) можно представить в дробно-рациональной форме

F(s) = N(s)/D(s)

и она имеет конечное число простых полюсов, то z-преобразование может быть получено по следующей формуле:

( 9 )

Если функция F(s) имеет кратные полюсы s₁, s₂, … , s_k с кратностью m₁, m₂, … , m_k соответственно, то z-преобразование F(s) следует рассчитывать по формуле:

(10)

где

(11)

3.2.2. Вычисление z-преобразования

Выражения (8), (9) и (10) можно использовать для вычисления z-преобразований. Выражение (8) применяют, если задано f(t) или f(nT). Строго говоря, на временные функции или ряды никакие ограничения не накладывается, хотя для того, чтобы F(z) можно было выразить в компактной форме, бесконечный ряд в выражении (8) должен сходиться. Выражения (9) и (10) определяют z-преобразования функций, заданных в виде преобразований Лапласа F(s). Выражение (9) используется для функции F(s), которая имеет только простые полюсы, а (10) — для функции, которая имеет, по крайней мере, один кратный полюс.

Следующие примеры иллюстрируют нахождение z-преобразований для некоторых часто встречающихся функций. В инженерной практике полезно использовать таблицы z-преобразований, которые можно найти в справочниках и учебниках.

Пример 1. Найдем z-преобразование единичной ступенчатой функции u_s(t). Следуя процедуре нахождения z-преобразования, изложенной в предыдущем параграфе, получим следующее:

1) единичная ступенчатая функция квантуется идеальным квантователем, при этом его выходным сигналом является последовательность единичных импульсов, описываемая как

2) применение преобразования Лапласа к обеим частям последнего выражения дает

где ряд сходится для |e^-Ts | < 1, а чтобы выразить u_s(t) в компактной форме, умножим обе части на e^-Ts и вычтем результат из последнего выражения, тогда

для |e-^Ts| < 1.

3) замена e^Ts на z дает

для |z -1| <1 или |z | >1.

4