лекции / Лекции дсау / ДСАУ 2_3

2. Основы математического аппарата и общие принципы построения импульсных систем. Дискретные процессы и их описание.___________________________________

2.3. Дискретные процессы и их описание

2.3.1. Решетчатые функции

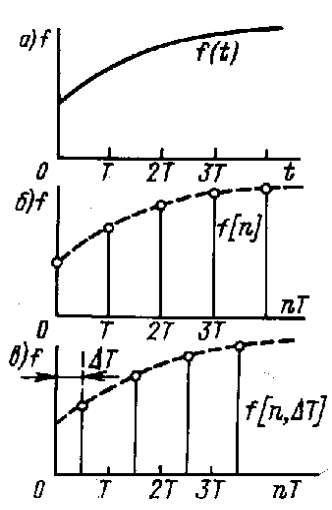
Решетчатой функцией называют функцию времени f[nT], или в сокращенной записи f[n], значения которой определены в дискретные моменты времени t = nT, где n – целое число, а Т – период повторения. Операция замены непрерывной функции решетчатой, представленная на рис. 2.19, может быть выражена как

f[n] = f(t)|_t=nT (2.23)

Рис. 2.19. Функции времени: а—непрерывная; б—дискретная; в — смещенная решетчатая

Непрерывная функция времени (рис. 2.19, а) служит для образования дискретной (решетчатой) (рис. 2.19, б). Изображенные на рис. 2.19, б ординаты исходной функции времени представляют собой дискреты, определенные для мо­ментов времени t=nT. Дискреты могут определяться также и для смещенных моментов времени t = nT + T = (n + ε)T. Смещение T = const может быть положительной или отрицательной величиной при выполнении условия |T| < T, или | ε | = |T/T| < 1. Образование смещенной решетчатой функции f[n, ε] из непрерывной функции f(t) для случая T>0 показано на рис. 2.19,в.

Решетчатая функция не обязательно должна формироваться из некоторой исходной непрерывной функции. Любая числовая последовательность некоторой величины, определенной в дискрет­ные равноотстоящие моменты времени, может трактоваться как решетчатая функция.

Обратная задача — формирование непрерывной функции из решетчатой — не может быть решена однозначно, так как функ­ции, заданной в дискретные моменты времени, может соответст­вовать бесконечное множество непрерывных функций. Непрерыв­ные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.

2.3.2. Прямая и обратная разности

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность

f[n] = f[n+1] – f[n], ( 1 )

либо первая обратная разность

f[n] = f[n] – f[n-1]. ( 2 )

Разности могут быть определены и для смещенных решетчатых функций f[n, ε].

Прямая разность определяется в момент времени t = nТ по будущему значению решетчатой функции при t = (n+1)T. Это можно сделать в тех случаях, когда будущее значение известно, либо, если это будущее значение нужно вычислить. Обратная разность определяется для момента времени t = nT по прошлому значению решетчатой функции в момент времени t = (n-1)T.

Аналогом второй производной непрерывной функции для решетчатой функции служат вторые разности:

прямая

²f[n] = f[n+1] - f[n] = f[n+2] – 2f[n+1] + f[n] ( 3 )

и обратная

²f[n] = f[n] - f[n-1] = f[n] – 2f[n-1] + f[n-2]. ( 4 )

Приведенные выше замечания относительно возможности вычисления прямой и обратной разностей сохраняют свою силу и здесь.

Аналогично формулам (1-4) могут вычисляться в выс­шие прямая и обратная разности. При этом получаются фор­мулы, у которых коэффициенты при членах совпадают с коэф­фициентами бинома Ньютона (см. например, формулы (3 ) и (4 )).

k ν

^kf[n] = Σ (-1)^ν C f[n-ν],

ν =0 k

k ν

^kf[n] = Σ (-1)^ν C f[n+k-ν],

ν =0 k

где биномиальные коэффициенты ( число сочетаний)

ν k!

C = ———— .

k ν !(k- ν)!

Обратные разности обладают важной особенностью. Если ре­шетчатая функция определена только для положительных зна­чений аргумента, т, е. f[n] ≡ 0 при п < 0, то в точке n = 0 k-я разность

^k[0] = f[0] ( 5 )

для любого целого положительного k.

Аналогами интеграла непрерывкой функции в пределах от 0 до t для решетчатой функции являются:

неполная сумма

n-1 n

σ[n] = Σ f[m] = Σ f[n-ν] ( 6 )

m=1 ν=1

и полная сумма

n

σ₀[n] = σ[n] + f[n] = σ[n+1] = Σ f[m] ( 7 )

m=0

Отличие (7) от (6) заключается в том, что значение f[n] в момент времени t = nT также участвует в формировании результата.

2.3.2. Разностные уравнения

В качестве аналогов дифференциальных уравнений можно рассматривать разностные уравнения (уравнения в конечных разностях).При использовании прямых разностей неоднородные разностные уравнения имеют следующий вид:

b₀^my[n] + b₁^m-1y[n] +… + b_my[n] = f[n] ,

где f[n] – заданная, а y[n] – искомая решетчатые функции.

При переходе к дискретам получаем

a₀y[n+m] + a₁y[n+m-1] +…+ a_my[n] = f[n]

Коэффициенты этого уравнения определяются из зависимости:

k k-ν

a_k = Σ (-1)^{k- ν} b _ν C ,

ν =0 m- ν

где биномиальные коэффициенты

k-ν (m- ν)!

C = ————— .

m- ν (k-ν)! (m-k)!

При использовании обратных разностей линейные неоднородные разностные

уравнения имеют вид:

b₀^my[n] + b₁^m-1y[n] +… + b_my[n] = f[n] , (8)

где f[n] – заданная, а y[n] – искомая решетчатые функции.

При f[n] ≡ 0 уравнение (8) становится однородным. Если по формулам (2), (4) и аналогичным, записанным для высших разностей, перейти к дискретам, то будет получено разностное уравнение в другом виде

a₀y[n] + a₁y[n-1] +…+ a_my[n-m] = f[n], (9)

k k-ν

a_m-k = Σ (-1)^m-k b _ν C ,

ν =0 m- ν

где биномиальные коэффициенты

k-ν (m- ν)!

C = ————— .

m- ν (k-ν)! (m-k)!

Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения у[n+m] при n = 0, 1, 2, ... для заданных начальных значений y[0], y[1], …, y[m-1] и уравнения вида (9). Такие вычисления легко выполняются на счетных машинах, а также не представляют никаких принципиальных трудностей и при ручном счете (кроме, конечно, затрат времени) даже и в случае, когда коэффициенты разностных уравнений a_i (i = 0, 1, …, m) с течением времени изменяются. Это отличает разностные уравнения от их непрерывных аналогов - дифференциальных уравнений.

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

y[n] = C₁zⁿ₁ + C₂zⁿ₂ + … + C_mzⁿ_m, (10)

где z_i (i = 1, 2, …, m) - корни характеристического уравнения

a₀z^m + a₁z^m-1 + … + a_m =0, (11)

а C_i – произвольные постоянные. Из (10), в частности, вытекает условие того, чтобы свободное движение системы, описываемой разностным уравнением (9), было бы затухающим (условие устойчивости):

|zi| < 1 (i = 1, 2, …, m). (12)

Для получения возможности исследования решений разностных уравнений в общем виде широко используется дискретное преобразование Лапласа, z-преобразование, w-преобразование, а также частотные методы.

Пример 1. Задана решетчатая функция f[n] = a, где a – постоянная величина. Найти первую разность данной функции.

По формуле (1) имеем

f[n] = f[n+1] – f[n] = a – a = 0,

т.е. первая разность от постоянной величины равна нулю.

Пример 2. Дана решетчатая функция f[n] = an + b, где a и b – постоянные величины. Определить первую разность этой функции.

По формуле (1) получим

f[n] = a[n+1]+b - a[n] - b = a ,

т.е. первая разность от линейной решетчатой функции есть постоянная величина. Вторая разность от функции f[n] = an + b равна нулю, действительно, ²f[n] = a = 0.

Пример 3. Дана решетчатая функция f[n] = n². Определить разности этой функции.

Получим

f[n] = (n+1)² – n² = 2n+1,

²f[n] = f[n+1] - f[n] = 2(n+1)+1 – 2n – 1 = 2,

³f[n] = 0.

т.е. вторая разность от степенной решетчатой функции n² постоянна, а разности более высокого порядка равны нулю.

Пример 4. Определить конечные разности экспоненциальной функции f[n] = e ^αn.

Аналогично предыдущему получаем:

f[n] = e ^{α (n+1)} – e ^αn = e ^αn(e ^α – 1),

²f[n] = (e ^α – 1) e ^αn = e ^αn (e ^α – 1)²,

продолжая процесс вычисления разностей, получаем следующую формулу для вычисления разности порядка k:

^kf[n] = e ^αn (e ^α – 1)^k.

4