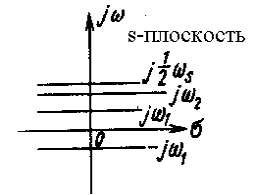лекции / Лекции дсау / ДСАУ 3_2_3

3. Дискретные преобразования и их основные свойства.

Z-преобразование_____________________________________________________________

3.2.3. Соответствие между s – и z-плоскостями.

Изучение соответствия между s- и z-плоскостями при преобразовании z = e^Ts является весьма важным. Проектирование непрерывных систем управления часто основывается на анализе распределения нулей и полюсов передаточной функции системы на s-плоскости. Аналогично, полюсы и нули z-преобразования передаточной функции определяют реакцию систе­мы в моменты замыкания. В этом параграфе рассмотрим отображение на z-плоскости заменой z = е^Ts некоторых часто используемых на s-плоскости кривых, таких, как линии постоянных коэффициента затухания и частоты и др.

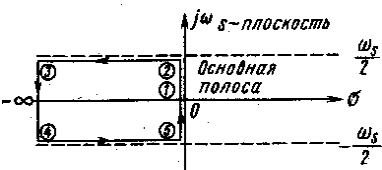
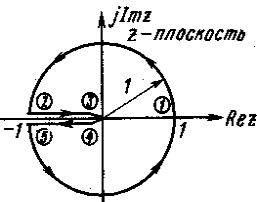
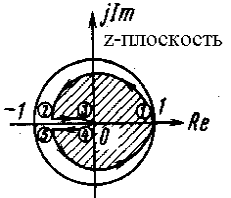
При рассмотрении свойств дискретного преобразования Лапласа (D-преобразования) было показано, что плоскость комплексного параметра q = sT делится на бесконечное число периодических полос. Основная полоса расположена в диапазоне – π < Im q  π. На плоскости комплексного параметра s основная полоса расположена в диапазоне частот от  = -_s/2 до + _s/2, где _s = 2/T. Дополнительные полосы расположены в диапазоне от -_s/2 до -З_s/2, от -З_s/2 до -5_s/2 и т.д. для отрицательных частот и от _s/2 до 3_s/2, от З_s/2 до 5_s/2 и т.д. для положительных частот. Если рассматривать только основную полосу (рис. 1, а), то контур (1) — (2) — (3) — (4) — (5) — (1), расположенный в левой половине s-плоскости, отображается преобразованием г = е^sT в единичную окружность на z-плоскости с центром в начале координат; как показано на рис. 1, б.

а)	б)

Рис. 1. Отображение основной полосы левой половины s-плоскости на z-плоскость

Так как

e^(s+jns)T = e^sTe^j2n = e^sT = e^q = z ( 1 )

для целых n, то все другие дополнительные полосы в левой половине s-плоскости отображаются в тот же самый единичный круг на z-плоскости. Все точки левой половины s-плоскости отображаются внутрь единичного круга на z-плоскости. Точки правой половины s-плоcкости отображаются в область вне единичного круга на z-плоскости.

Ниже рассматривается отображение на z-плоскость для цифровых систем линий постоянных затухания и частоты и коэффициента затухания.

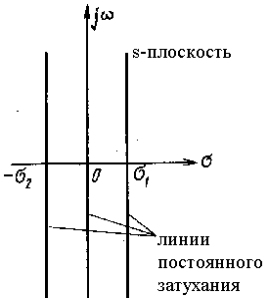
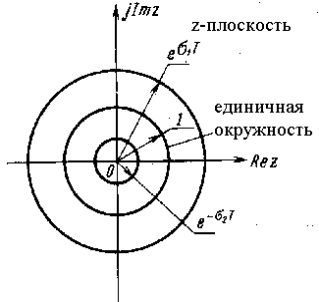
Линии постоянного затухания. Для постоянного затухания σ₁ на s-плоскости соответствующая кривая на z-плоскости представляет собой окружность с радиусом z = e^σ1T и с центром в начале координат (рис. 2).

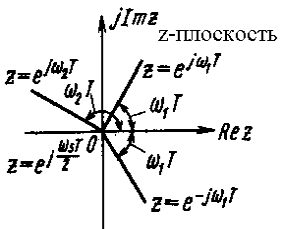
Линии постоянной частоты. Для любой фиксированной частоты ω = ω1 на s-плоскости соответствующая линия на z-плоскости (рис. 3) имеет вид луча, исходящего из начала координат под углом θ = ω₁T рад. Угол измеряется от положительного направления действительной оси.

а)	б)

Рис. 2. Линии постоянного затухания на s- и z-плоскостях

а)	б)

Рис. 3. Линии постоянной частоты на s- z-плоскостях

Линии постоянного коэффициента затухания. Линии, соответствующие постоянному коэффициенту затухания ξ на s-плоскости, описываются выражением

s = - ω tg β + jω. ( 2 )

На z-плоскости оно имеет вид

z = e^sT = exp(-2πω tgβ / ω_s) exp(j2πω / ω_s), ( 3 )

где β = arcsin ξ = const. ( 4 )

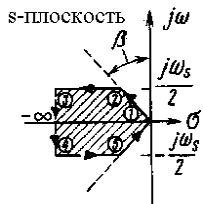
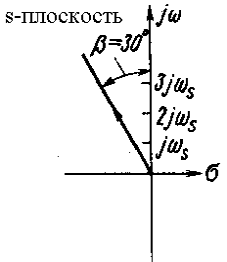
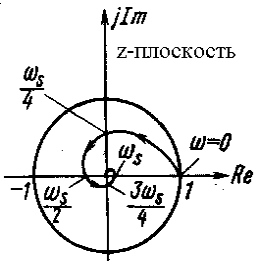
Для заданного угла β линия постоянного значения ξ, описываемая уравнением (3), представляет собой на z-плоскости логарифмическую спираль (кроме значений β = 0 и β = 90°). Отображение линии постоянного коэффициента затухания с s-плоскости на z-плоскость показано на рис. 4. Заштрихованные области на рис. 4, а и б соответствуют друг другу. На рис. 5 показаны линии на s- и z-плоскостях для β = 30°. Каждые пол-оборота логарифмической спирали соответствуют отрезку линии постоянного значения ξ на s-плоскости при изменении частоты по мнимой оси на ω_s/2.

а)	б)

Рис. 4. Линии постоянного коэффициента затухания на s- и z-плоскостях

а)	б)

Рис. 5. Линии постоянного коэффициента затухания для β = 30° (ξ = 0,5) на s- и z-плоскостях

3.2.4. Вычисление обратного z-преобразования.

Преобразование Лапласа и его обратное преобразование являются однозначными, т.е. если F(s) есть преобразование Лапласа для функции f(t), то f(t) является обратным преобразованием Лапласа для функции F(s). Для z-преобразования обратное z-преобразование не является однозначным. z-Преобразование f(t) определяется функцией F(z), а обратное z-преобразование не обязательно равно f(t). Корректный результат обратного z-преобразования функции F(z) есть f(kT), который равен f(t) только в моменты квантования t = kT.

Рис. 6 иллюстрирует тот факт, что для z-преобразования единичной ступенчатой функции, которое равно z/(z-1) и соответствует последовательности единичных импульсов, обратное z-преобразование может быть любой функцией, значения которой равны единице в моменты t = 0, T, 2T, … . Неоднозначность обратного z-преобразования является одним из ограничений, о котором необходимо помнить при применении аппарата z-преобразования.

Обратное z-преобразование обозначается как

F(kT) = Z^-1[F(z)] = обратное z-преобразование F(z).

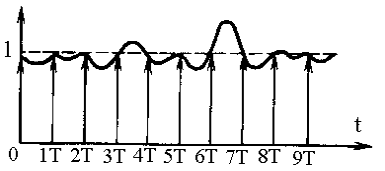
Рис. 6. Неоднозначность обратного z- преобразования

В общем случае обратное z-преобразование может быть определено одним из следующих трех методов.

1. Метод разложения на простые дроби. Этот метод при небольшой модификации соответствует методу разложения на простые дроби в преобразовании Лапласа. При анализе непрерывных систем обратное преобразование Лапласа функции F(s) может быть получено разложением F(s) в виде

A B C

F(s) = ——— + ——— + ——— + … ( 5 )

s + a s + b s + c

где a, b, и c - отрицательные полюсы F(s) (здесь предполагается случай простых полюсов); А, В и С — вычеты F(s) в этих полюсах. Тогда обрат­ное преобразование Лапласа функции F(s) определяется как

f(t) = Ae^-at + Be^-bt + Ce^-ct + … ( 6 )

Для случая z-отображения F(z) не надо представлять в форме (5). Дело в том, что в таблице z-преобразований обратное z-преобразование для выражения вида A/(z + a) отсутствует, хотя при положительном значении а член такого вида соответствует последовательности импульсов с экспоненциально затухающей амплитудой, когда присутствует временная задержка. Вместе с тем известно, что обратное z-преобразование функции Az/(z – e^-aT) равно Ae^-akT, Следовательно, удобнее разложить на простые дроби функцию F(z)/z. После разложения обе части выражения для F(z)/z умножают на z для получения F(z).

Для функции, которые не содержат нулей (z = 0), соответствующая последовательность импульсов имеет временной сдвиг. Разложение функции F(z) на простые дроби представляются в обычном виде, т.е.

A B C

F(z) = ——— + ——— + ——— + … ( 7 )

z + a z + b z + c

После чего находим

Az Bz Cz

F1(z) = zF(z) = ——— + ——— + ——— + … ( 8 )

z + a z + b z + c

Если найдено обратное z-преобразование функции F₁(z), f₁(kT), то обратное z-преобразование функции F(z) определяется следующим образом:

F(kT) = Z^-1[F(z)] = Z^-1[z^-1F₁(z)] = f₁[(k – 1)T]. ( 9 )

Пример 5. Найти обратное z-преобразование для

(1 – e^-aT)z

F(z) = ———————

(z – 1)(z - e^-aT)

где а - положительное постоянное число; T - период квантования. Используя ме­тод разложения на простые дроби, найти обратное z-преобразование F(z),f(kT). Разложение F(z)/z на простые дроби дает

следовательно,

Из таблицы z-преобразований может быть найдено обратное z-преобразование F(z) виде временной функции, значения которой в моменты квантования определяются как f(kT) = 1 – e^-akT,

следовательно, дискретная временная функция может быть записана в виде



F*(t) = Σ (1 –e^-akT)δ(t –kT).

k=0

Заметим, что временная функция f(t) не может быть определена из обратного z-преобразования, так как оно не определяет значения функции между моментами замыкания.

2. Метод разложения в степенной ряд. Из определения z-преобразования следует, что обратное z-преобразование F(z) может быть определено разложением её в бесконечный ряд по степеням z^-1:

F(z) = f(0) + f(T)z^-1 + f(2T)z^-2 + … + f(kT)z^-k + … (10)

Следовательно, коэффициенты ряда соответсвуют значениям f(t) в мо­менты квантования. Основное различие между методами разложения на простые дроби и в степенной ряд заключается в том, что первый метод дает решение для f(kT) в компактной форме, в то время как решением второго метода является последовательность чисел. Разумеется, оба ме­тода эквивалентны, и для последовательности чисел также может быть записано выражение в компактной форме.

Пример 6. Определить обратное z-преобразование функции

(1 – e^-aT)z

F(z) = ——————————

z² – (1 + e^-aT)z + e^-aT

заметим, что эта функция совпадает с функцией из предыдущего примера 5.

Последовательное деление числителя на знаменатель дает:

F(z) = (1 – e^-aT)z^-1 + (1 – e^-2aT)z^-2 + …

В этом случае легко видеть, что f(kT) = 1 – e^-akT k = 0, 1, 2, …,

Следовательно,



F*(t) = Σ (1 –e-akT)δ(t –kT),

k=0

что совпадает с результатом предыдущего примера, полученным методом разложения на простые дроби.

2. Метод, основанный на использовании формулы обращения. Также, как и для непрерывных функций можно найти оригинал по его изображению с помощью обратного преобразования Лапласа, так и для обратного z-преобразования существует аналогичное выражение.

9