17.Подпространство

Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают какLat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

• ;

• для всякого вектора 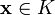, вектор  также принадлежал K, при любом ;

• для всяких векторов , вектор  также принадлежал K.

Последние два утверждения эквивалентны следующему:

• для всяких векторов , вектор  также принадлежал K для любых .

В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.

Свойства подпространств:

• Пересечение любого семейства подпространств — снова подпространство;

• Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств  определяется как множество, содержащее всевозможные суммы элементов K_i:

.

18.Линейно-зависимые и линейно-независимые системы векторов

Пусть имеем векторное пространство V и систему векторов A={} (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор  называется линейной комбинацией системы векторов A. Если все скаляры α₁ = α₂ = α₃... = α_k = 0, то такая комбинация называется тривиальной (простейшей), (и ). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной.

• Определение 1: система векторов A называется линейно-независимой, если только тривиальная линейная комбинация векторов системы равна , (т.е.  )

• Определение 2: система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная .

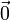Свойства

1. Cистема векторов A линейно-зависима ↔ один из её векторов равен  или один из векторов есть линейная комбинация прочих векторов системы.

Доказательство

(→): если A линейно-зависима, то, по определению, не все коэффициенты в   (1) комбинации равны 0. (Для определённости запишем комбинацию так, чтоб сначала шли ненулевые коэффициенты, а потом нулевые). Возможны два случая: 1)только первый коэффициент не нулевой, 2)два и более коэффициента не нулевые. В первом случае получаем , откуда . Во втором случае равенство (1) принимает вид   (2). Т.к. все коэффициенты от α₁до α_jв (2) не равны 0, то (2) можно переписать так , т.е. один из векторов линейно выражен через другие векторы.

2.  Если система A содержит линейно-зависимую подсистему, то и вся система A линейно-зависима. В частности, система векторов линейно-зависима, если она содержит нулевой вектор, или равные векторы, или пропорциональные (коллинеарные) векторы

3.  Если A- линейно-независимая система векторов, а система  линейно-зависима, то  есть линейная комбинация системы векторов A

4.  Пусть даны две системы A={} (3), B={} (4) при этом: 1) A-линейно-независимая система векторов  2) каждый вектор системы A линейно выражается через B. Тогда число векторов системы A не превосходит числа векторов системы B, т.е. k≤i.

Доказательство

Прежде отметим, что 1) всякий вектор данной системы может быть линейно выражен через векторы этой же системы. Например, для системы A (3)  2)Если некий  линейно выражается через систему A, а A выражается через B, то  можно выразить и через B, т.е. отношение "линейно выражаться через"для системы векторов является транзитивным (переходящим).

Перейдём теперь непосредственно к доказательству. Припишем к системе B слева вектор :

   (4)

.Т.к.  линейно выражается через B, то B-линейно-зависимая система. Поскольку  (иначе A линейно-зависима), то один из векторов системы B, согласно свойству 1, линейная комбинация прочих векторов системы (4). Пусть для определённости это будет . Выбросим  из (4):

  (5)

. Вектор  линейно выражается через (5)— он по этой причине выброшен из (4), остальные векторы из B входят в (5), а значит, согласно первому замечанию, тоже линейно выражаются через (4). Значит вся система B линейно выражается через (5), а по транзитивности через (5) линейно выражается и система векторов A. Следовательно, если к (5)приписать слева вектор , то получим линейно-зависимую систему векторов:

  (6)

. Т.к. , то по свойству 1, один из векторов системы (6) линейная комбинация прочих векторов системы (6). Пусть для определённости это будет . Выбросим  из(6). Будем продолжать описанный выше процесс замещения векторов системы B векторами из A. Допустим, что k>l. Тогда после l-шага векторы системы B исчерпаются и мы получим систему векторов , приписывая к которой вектор , мы получим линейно-зависимую систему векторов, являющейся подсистемой системы A. Но тогда, по свойству 2, A-линейно-зависима. Значит , неверно, что k>l, остаётся, что k ≤ l, ч.т.д.