1.Понятие комплексного числа, его вещественная и мнимая часть

Определение. Комплексным числом называется выражение вида a + bi, где a и b – произвольные вещественные числа, а i – специальный символ.

Вещественные числа а и b называют соответственно вещественной и мнимой частями комплексного числа z = a + bi. Комплексное число, у которого мнимая часть равна нулю, т. е. комплексное число вида a + 0i записывают в виде а и отождествляют с вещественным числом а. Обозначение: a = Re z, b = Im z.

Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z2 + 1 имеет корень.

2.Модуль и аргумент комплексного числа.

2. Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа z обозначается | z | и определяется выражением . Часто обозначается буквами или . Если z является вещественным числом, то | z | совпадает с абсолютной величиной этого вещественного числа.

Для любых имеют место следующие свойства модуля. :

1) , причём тогда и только тогда, когда ;;

2) (неравенство треугольника);

3) ;

4) .

Из третьего свойства следует , где . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем .

5) Для пары комплексных чисел z₁ и z₂ модуль их разности | z₁ − z₂ | равен расстоянию между соответствующими точками комплексной плоскости.

Угол (в радианах) радиус-вектора точки, соответствующей числу z, называется аргументом числа z и обозначается .

• Из этого определения следует, что ; ; .

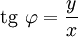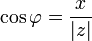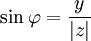• Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2kπ, где k — любое целое число.

• Главным значением аргумента называется такое значение , что . Часто главное значение обозначается 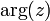. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: .

• 

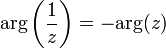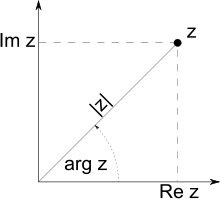
Модуль, аргумент, вещественная и мнимая части

3. Геометрическая модель

Геометрическое представление комплексного числа

Рассмотрим плоскость с прямоугольной системой координат. Каждому комплексному числу сопоставим точку плоскости с координатами {x,y} (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.

Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже.

В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».