Свойства

• Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

• Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:

Пример

Скалярное произведение векторов — симметричная билинейная функция. Соответствующая квадратичная функция сопоставляет вектору квадрат его длины.

54.Нормальный вид квадратичной формы над полем действительных чисел.

Определение. Квадратичной формой  переменных ,принимающих числовые значения , называется числовая функция вида

  ,

где - числа, называемые коэффициентами квадратичной формы.

Определение. Матрицей квадратичной формы  переменных , называется симметрическая матрица порядка , элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в ой строке ом столбце, равен половине коэфициента при  в квадратичной форме.

Определение. Рангом квадратичной формы называется ранг её матри-цы. Квадратичная форма может быть записана в матричном виде  где матрица квадратичной формы и .

Определение. Квадратичная форма называется канонической (имеет канонический вид), если коэфициенты при , то есть, если матрица квадратичной формы диагональная и следовательно

.,

где не все коэффициенты   равны нулю.

Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.

Определение. Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны .

55.Закон инерции квадратичных форм.

Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.

Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы

56.Положительно и неотрицательно определенные квадратичные формы над полем действительных чисел.

• Квадратичная форма Q называется положительно (отрицательно) определённой, если для любого Q(x) > 0 (Q(x) < 0).

  • Положительно определённые и отрицательно определённые формы называются знакоопределёнными.

  • Квадратичная форма A(x,x) называется знакопеременной, если она принимает как положительные, так и отрицательные значения.

  • Квадратичная форма Q называется полуопределенной, если .

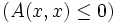57.Критерий Сильвестра положительной определенности квадратичной формы.

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма  была положительно определённой, необходимо и достаточно чтобы все угловые миноры (см. ниже) матрицы квадратичной формы были положительны, то есть, чтобы

Здесь -угловые миноры матрицы квадратичной формы.

Следствие. Для того чтобы квадратичная форма  была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались следующим образом:

Минор 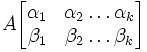матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами и столбцов с номерами .

Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.

Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.

Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.