Следствие

Если непрерывная функция обращается в ноль в n различных точках, то ее производная обращается в ноль по крайней мере в n − 1 различных точках, причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.

40Теорема Лагранжа.

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка , что

Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Механическое истолкование: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение — средняя скорость за этот промежуток.

Доказательство

Для функции одной переменной:

Введем функцию . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю:

56. Теорема Коши.

Теорема Коши́ о среднем значении.

Пусть даны две функции и такие, что:

1. и определены и непрерывны на отрезке ;

2. производные и конечны на интервале ;

3. производные и не обращаются в нуль одновременно на интервале

4. ;

тогда

, где

(Если убрать условие 4, то необоходимо усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале (a,b).)

Геометрически это можно переформулировать так: если f и g задают законы движения на плоскости (то есть определяют абсциссу и ординату через параметр t), то на любом отрезке такой кривой, заданном параметрами a и b, найдётся касательный вектор, коллинеарный вектору перемещения от (f(a);g(a)) до (f(b);g(b)).

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а равна как раз необходимому числу.

42Правило Лопиталя.

Правило Лопита́ля - метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Теорема верна для разных баз. Определение приведено для предела (при стремлении) к точке справа, но то же справедливо для предела слева и двустороннего предела и для предела к бесконечностям, a не к точке. Для использованной в определении базы "к точке a справа" ниже будет приведено доказательство.

Правило говорит, что если функции f(x) и g(x) обладают следующим набором условий:

1. или ;

2. Если g(x) и f(x) — дифференцируемы в проколотой окрестности a;

3. в проколотой окрестности a;

4. существует ,

тогда существует .

Примеры

• 

• Здесь можно применить правило Лопиталя 3 раза, а можно поступить иначе. Можно разделить и числитель, и знаменатель на x в наибольшей степени(в нашем случае x³). В этом примере получается:

• ;

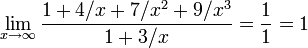
• при a > 0.

(Только если числитель и знаменатель ОБА стремятся или к 0; или к ; или к .)

42. Правила дифференцирования.

Пусть c – постоянная, f(x) и g(x) – дифференцируемые функции, тогда

c = 0;

(c * f(x))’ = c * (f(x))’;

(f(x) ⁺ g(x))’ = f ‘(x) ⁺ g ‘(x);

(f(x) * g(x))’ = f ‘(x) * g(x) + f(x) * g ‘(x);

(f(x)/g(x))’ = (f ‘(x) * g(x) – f(x) * g ‘(x))/g²(x);

Если функции  f и g дифференцируемы в точке то в этой же точке дифференцируемы сумма, произведение и частное (если этих функций, причем

1. (f+g =

2. (fg =

3. 

Постоянный множитель C можно выносить из-под знака производной: (Cf)' = Cf'. В частности, С'=0

• Если f дифференцируема, то где n N также дифференцируема, причем

• Если функция y = f (x) непрерывна и строго возрастает в окрестности точки причем, то функция x = φ (y),обратная к функции y = f (x), дифференцируема в точке= f (), причем

• Если функции y = f (x) и z = g (y) дифференцируемы в точках и = f () соответственно, то сложная функция z = g ( f (x)) дифференцируема в точке x ₀, причем z()=g() f().

• Дифференциал функции y = f (x) имеет один и тот же вид dy=f(x)dx как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.

• Если f (x) – четная функция, то f(x) – нечетная; если f (x ) – нечетная функция, то f(x) – четная.

• Пусть в окрестности точки t ₀ определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна. Пусть в этой окрестности существуют производные и Тогда сложная функция y = y ( t ( x )), где t ( x ) – функция, обратная x (t), дифференцируема по x , причем .