38Определение дифференциала функций. Правила нахождения дифференциала.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.                                             (1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (1) можно записать так: dy=ƒ'(х)dх,                                              (2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (2) следует равенство dy/dx=ƒ'(х). Теперь обозначение производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.

Правила для вычисления дифференциала - прямое следствие правил дифференцирования :

1. ;

2. ;

3. ;

4. .

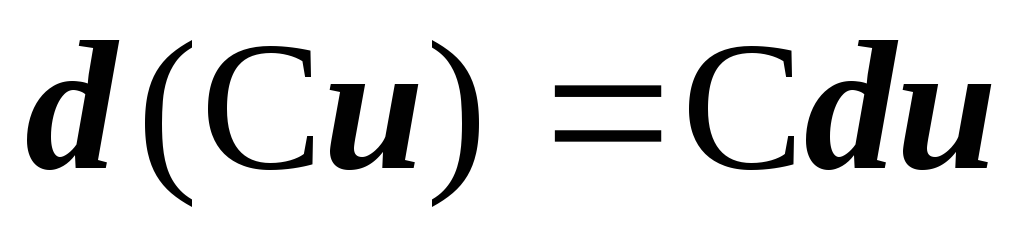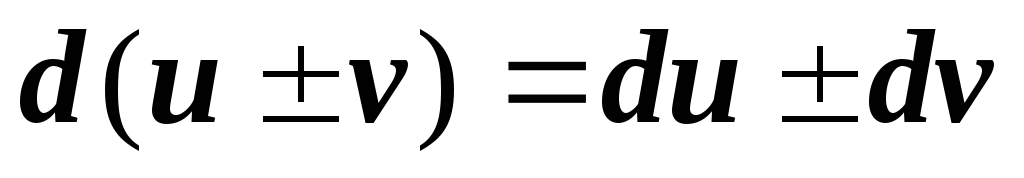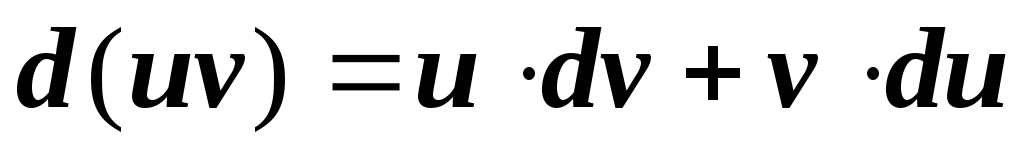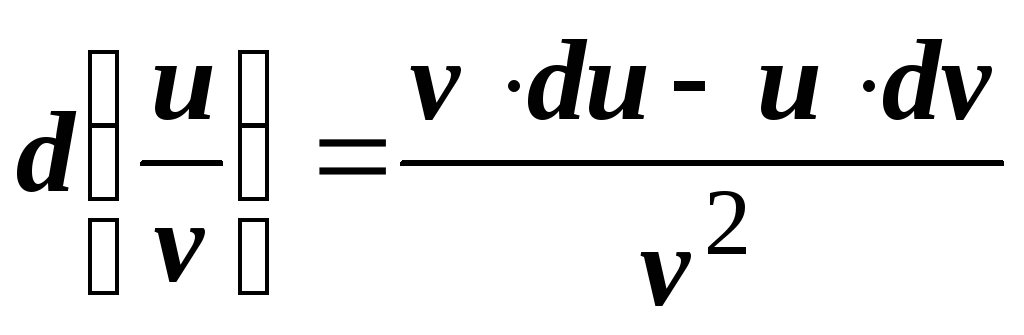38 Дифференциал сложной функции.

Инвариантная форма записи дифференциала.

 Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f(x)g(t)dt = f(x)dx.

 Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

 Однако, если х- независимая переменная, то dx = x, но если х зависит от t, то х  dx.

Таким образом форма записи dy = f(x)x не является инвариантной.

56. Инвариантность формы первого дифференциала.

Дифференциал функции z = g(y) в точке y₀ имеет вид: где dy — дифференциал тождественного отображения :

Пусть теперь Тогда , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

Пример

Пусть h(x) = (3x² − 5x)⁷. Тогда функция h может быть записана в виде композиции где

Дифференцируя эти функции отдельно:

получаем

37. Непрерывность основных элементарных функций. Точки разрыва и их классификации

Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.

Теорема 1 . Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).

Пусть функция ƒ(х) и φ(х) непрерывны на некотором множестве X и x₀ — любое значение из этого множества. Докажем, например, непрерывность произведения F(x)=ƒ(х)•φ(х). Применяя теорему о пределе произведения, получим: Итак,  что и доказывает непрерывность функции ƒ(х)•φ(х) в точке х₀.

Теорема 2 . Пусть функции u=φ(х) непрерывна в точке х₀, а функция у=ƒ(u) непрерывна в точке u₀=φ(х_о). Тогда сложная функция ƒ(φ(х)), состоящая из непрерывных, функций, непрерывна в точке х₀.

В силу непрерывности функции u=φ(х)  

т. е.при х→х₀ имеем u→u₀. Поэтому вследствие непрерывности функции у=ƒ(u) имеем:

Это и доказывает, что сложная функция у=ƒ(φ(х)) непрерывна в точке х₀.

Теорема 3 . Если функция у=ƒ(х) непрерывна и строго монотонна на [a;b] оси (Oх, то обратная функция у=φ(х) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу (без доказательства).

Так, например, функция tgx=sinx/cosx . в силу теоремы 19.1, есть функция непрерывная для всех значений х, кроме тех, для которых cosх=0, т. е. кроме значений х=π/2+πn, nєZ.

Функции arcsinx, arctgx, arccosx, arcctgx, в силу теоремы 19.3, непрерывны при всех значениях х, при которых эти функции определены.

Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.

Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.

Если хотя бы одно из равенств  нарушается, говорят о разрыве в точке . Если  и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.