
- •69. Интегрирование тригонометрических выражений с помощью тригонометрических подстановок.
- •70. Интегрирование простейших иррациональных функций.
- •71. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок.
- •72. Некоторые интегралы, не выражающиеся в элементарных функциях.
- •74. Интегральные суммы. Определение определенного интеграла. Интегральные суммы.
- •79. Геометрическое применение определенного интеграла.
- •80. Понятие о несобственных интегралах.
- •63. Непосредственное интегрирование.
- •64. Метод интегрирования с помощью замены.
- •65. Метод интегрирования по частям.
- •66. Понятие дробно-рациональной функции. Простейшие рациональные дроби.
- •67. Правильные и неправильные дроби. Процесс деления и выделения целой части для неправильной дроби.
- •68. Разложение правильной дроби в сумму простейших дробей.
- •69. Интегрирование тригонометрических выражений с помощью тригонометрических подстановок.
- •III. Интегрирование выражений вида sin (αx) · sin (βx) , sin (αx) · cos (βx) , cos (αx) · cos (βx) .
- •Возрастание и убывание функции.
- •46Выпуклость и вогнутость функции.
- •Экстремумы функции.
- •46Асимптоты функции.
- •Виды асимптот графиков
- •Исследование функций и построение графиков.
- •61. Первообразная функции. Неопределенный интеграл.
- •39Применение дифференциала для приближенных вычислений.
- •Теорема Ферма.
- •41Теорема Ролля.
- •Геометрический смысл:Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
- •Следствие
- •40Теорема Лагранжа.
- •Доказательство
- •Теорема Коши.
- •Доказательство
- •42Правило Лопиталя.
- •Примеры
- •36. Производная неявной функции.
- •45. Производная параметрически заданной функции.
- •37 Производные высших порядков.
- •38Определение дифференциала функций. Правила нахождения дифференциала.
- •38 Дифференциал сложной функции.
- •Инвариантность формы первого дифференциала.
- •37. Непрерывность основных элементарных функций. Точки разрыва и их классификации
- •27. Задачи, приводящие к понятию производной
- •28 Определение производной, ее геометрический и механический смысл
- •40. Касательная к кривой на плоскости
- •41. Зависимость между непрерывностью и дифференцируемостью функции.
- •27. Определение предела функции.
- •Определения
- •28. Бесконечно малые и бесконечно большие величины. Связь между ними.
- •29. Свойства бесконечно малых величин.
- •30. Односторонние пределы
- •23. Основные теоремы о пределах.
- •32. Раскрытие неопределенностей
- •25. Первый замечательный предел
- •26. Второй замечательный предел
- •35. Приращение аргумента и функции. Определение непрерывности функции в точке
- •36. Определение непрерывности функции на промежутке. Основные теоремы о непрерывных функциях
- •19. Угол между прямыми на плоскости.
- •21. Уравнение прямой, проходящей через две точки.
- •22. Расстояние от прямой до точки на плоскости.
- •21???. Определение функции. Область определения, способы задания функции.
- •25. Свойства функций.
- •26. Последовательности, определение предела последовательности.
- •9. Условия совместности и определенности систем линейных уравнений.
- •19. Теорема Кронекера-Капелли.
- •11. Решение системы n линейных уравнений с m неизвестными.
- •14. Решение систем линейных уравнений методом Гаусса.
- •4. Скалярное произведение векторов.
- •1. Расстояние между двумя точками. Коллинеарные вектора.
- •17. Деление отрезка в данном отношении.
- •15Матрицы. Действия с матрицами.
- •4. Разложение определителей по элементам строк и столбцов.
- •16. Понятие обратной матрицы.
- •Свойства обратной матрицы
- •17. Метод обратной матрицы решения систем линейных уравнений.
- •13 . Правило Крамера решения систем линейных уравнений.
- •Решение системы находим по формулам Крамера
- •19. Понятие ранга матрицы. Его нахождение.
72. Некоторые интегралы, не выражающиеся в элементарных функциях.
а) Дифференциальные биномы
(a+bxn)pxm, когда не
является целой ни одна из трех дробей
p,
![]()
![]() ,
,
![]() +p.
+p.
б) Интеграл
![]() .
.
в) Интегралы вида
![]() ,
где - многочлен степени 3, 4 в ряде
случаев не выражается через элементарные
функции (эллиптические интегралы ). В
частности, следующие интегралы не
являются элементарными функциями
,
где - многочлен степени 3, 4 в ряде
случаев не выражается через элементарные
функции (эллиптические интегралы ). В
частности, следующие интегралы не
являются элементарными функциями
![]() ,
,
![]() ,
0<k<1;
,
0<k<1;
или ( после замены )
![]() ,
,
![]() .
.
74. Интегральные суммы. Определение определенного интеграла. Интегральные суммы.
Для
каждого разбиения отрезка [a;b] точками
x1=a,x2,x3,…,xn-1,xn=b
в каждой части [xk;xk+1]
выбирается произвольная точка ck,
вычисляется значение f(ck)
и составляется следующая сумма:
![]()
![]()
Суммы вида Σn называют интегральными суммами для функции f(x) на отрезке [a;b].
79. Геометрическое применение определенного интеграла.
Вычисление площадей и длин дуг кривых в декартовых координатах.
Пусть
на плоскости
![]() задана
область, ограниченная снизу кривой
задана
область, ограниченная снизу кривой
![]() ,
заданной в декартовых координатах,
сверху – кривой
,
заданной в декартовых координатах,
сверху – кривой
![]() ,
слева – прямой
,
слева – прямой
![]() (ее
может и не быть, если
(ее
может и не быть, если
![]() ),
справа – прямой
),
справа – прямой
![]() .
Исходя из геометрического
смысла определенного интеграла,
площадь этой области можно вычислить
по формуле
.
Исходя из геометрического
смысла определенного интеграла,
площадь этой области можно вычислить
по формуле
![]() .
Здесь не нужно заботиться, какая из
функций и где положительная, а какая
отрицательная. Если, например,
.
Здесь не нужно заботиться, какая из
функций и где положительная, а какая
отрицательная. Если, например,
![]() ,
то формула сама прибавит нужную площадь.
Более сложные области всегда можно
разбить так, чтобы выполнялись указанные
условия.
,
то формула сама прибавит нужную площадь.
Более сложные области всегда можно
разбить так, чтобы выполнялись указанные
условия.
Пусть
на отрезке
![]() уравнением
уравнением
![]() задана
плоская кривая. Ее длина вычисляется
по формуле
задана
плоская кривая. Ее длина вычисляется
по формуле
![]()
Вычисление площадей и длин дуг при параметрическом задании кривых.
Если
область на плоскости снизу ограничена
кривой,
заданной параметрически,
то есть
![]() ,
при этом
,
при этом
![]() ,
а сверху – кривой
,
а сверху – кривой
![]() .
Тогда площадь такой плоской фигуры
вычисляем по формуле
.
Тогда площадь такой плоской фигуры
вычисляем по формуле
![]() .
Эта формула совпадает с формулой
вычисления площади в декартовых
координатах, если учесть, что
.
Эта формула совпадает с формулой
вычисления площади в декартовых
координатах, если учесть, что
![]() .
.
Пусть
кривая на плоскости задана параметрически
![]()
![]() .
Тогда длина этой кривой вычисляется по
формуле
.
Тогда длина этой кривой вычисляется по
формуле
![]() .
.
Вычисление площадей и длин дуг кривых в полярных координатах.
Когда
кривая, ограничивающая область, задана
в полярных
координатах
![]() ,
то площадь этой области вычисляем по
формуле
,
то площадь этой области вычисляем по
формуле
![]() .
Основная трудность в использовании
этой формулы заключается в определении
пределов интегрирования
.
Основная трудность в использовании
этой формулы заключается в определении
пределов интегрирования
![]() .
Здесь нужно понимать, что кривая
.
Здесь нужно понимать, что кривая
![]() определена
только, если
определена
только, если
![]() .
Поскольку в формуле присутствует
.
Поскольку в формуле присутствует
![]() ,
то она учтет и не существующую площадь,
когда
,
то она учтет и не существующую площадь,
когда
![]() .
Решив уравнение
.
Решив уравнение
![]() ,
найдем пределы интегрирования.
,
найдем пределы интегрирования.
Если
кривая, ограничивающая область, задана
в полярных координатах
![]() ,
то ее длина вычисляется по формуле
,
то ее длина вычисляется по формуле![]() . Пределы интегрирования определяются
из тех же соображений, что и при вычислении
площади.
. Пределы интегрирования определяются
из тех же соображений, что и при вычислении
площади.
80. Понятие о несобственных интегралах.
До
сих пор предполагалось, что, во-первых,
областью интегрирования для определенного
интеграла служит конечный отрезок
![]() ,
а во-вторых, что подынтегральная функция
интегрируема на этом отрезке. Отбрасывая
эти предположения, приходим к понятию
несобственных
интегралов
двух типов: по бесконечному промежутку
и от неограниченной функции. Как
противопоставление несобственным
интегралам, обычные определённые
интегралы,
которые вычисляются от интегрируемых
(ограниченных) функций и по конечным
отрезкам, часто называют собственными
интегралами.
,
а во-вторых, что подынтегральная функция
интегрируема на этом отрезке. Отбрасывая
эти предположения, приходим к понятию
несобственных
интегралов
двух типов: по бесконечному промежутку
и от неограниченной функции. Как
противопоставление несобственным
интегралам, обычные определённые
интегралы,
которые вычисляются от интегрируемых
(ограниченных) функций и по конечным
отрезкам, часто называют собственными
интегралами.
Определение:
Пусть
f(x)
определена на множестве от
![]() и
и
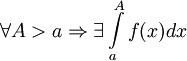 .
Тогда:
.
Тогда:
-
Если
 ,
то используется обозначение
,
то используется обозначение
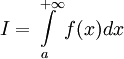 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
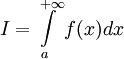 называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
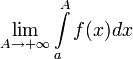 (
( или
или
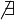 ), то интеграл
), то интеграл
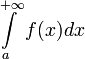 называется
расходящимся к
называется
расходящимся к
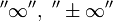 ,
или просто расходящимся.
,
или просто расходящимся.
Пусть
f(x)
определена на (a,b]
и
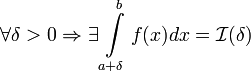 .
Тогда:
.
Тогда:
-
Если
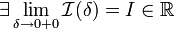 ,
то используется обозначение
,
то используется обозначение
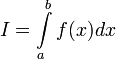 и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся. -
Если
 или
или
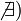 ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а
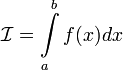 называется
расходящимся к
называется
расходящимся к
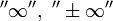 ,
или просто расходящимся.
,
или просто расходящимся.
