23. Основные теоремы о пределах.

  Теорема 1. , где С = const.

  Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

  Теорема2. 

Доказательство этой теоремы будет приведено ниже.

  Теорема3. 

  Следствие. 

   Теорема4.  при 

  Теорема 5. Если f(x)>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

  Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и , то и .

   Определение. Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

  Теорема 7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а.

32. Раскрытие неопределенностей

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа: ,,, ,,,    по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов , ,  пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

25. Первый замечательный предел

Первым замечательным пределом называется предел

    

        Теорема 2.14   Первый замечательный предел равен

Следствия

• 

• 

• 

• 

26. Второй замечательный предел

Второй замечательный предел — это формула, где e = 2,718281828... — основание натуральных логарифмов.

Следствия

• 

• 

• 

•  для ,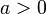 

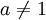
35. Приращение аргумента и функции. Определение непрерывности функции в точке

Рассмотрим функцию y = f(x). Пусть x₀D(f) – фиксированная точка; xD(f) – произвольная точка.

Определения. 1) x = x – x₀ называется приращением аргумента в точке x₀.

Очевидно, что если x > x₀, то x > 0, а если x < x₀, то x < 0

2) f(x₀) = f(x) – f(x₀) = f(x₀ + x) – f(x₀) называется приращением функции в точке x₀

Непрерывность функции в точке

Пусть функция у=ƒ(х) определена в точке х_о и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е. (1)

Равенство (1) означает выполнение трех условий: 1) функция ƒ (х) определена в точке x₀ и в ее окрестности; 2)  функция ƒ(х) имеет предел при х→х_о; 3)  предел функции в точке х_о равен значению функции в этой точке, т. е. выполняется равенство (1).

Так как    то равенство (19.1) можно записать в виде(2)

Это означает, что при нахождении предела непрерывной функции ƒ(х) можно перейти к пределу под знаком функции, то есть β функцию ƒ(х) вместо аргумента х подставить его предельное значение х_о.