4. Разложение определителей по элементам строк и столбцов.
Определитель
равен сумме произведений элементов
какой-либо строки или столбца на их
алгебраические дополнения.Используя
эту теорему, запишем разложение
определителя третьего порядка по первой
строке.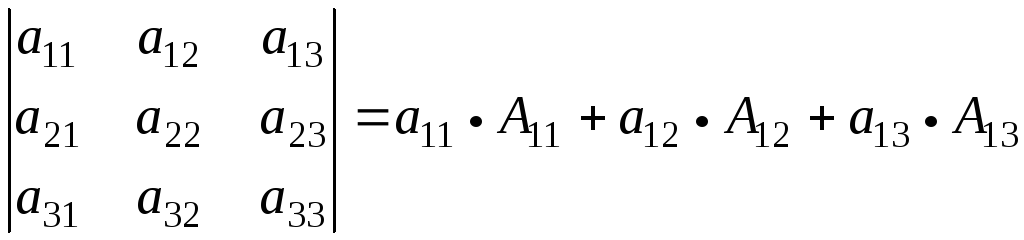
.
В развернутом виде:
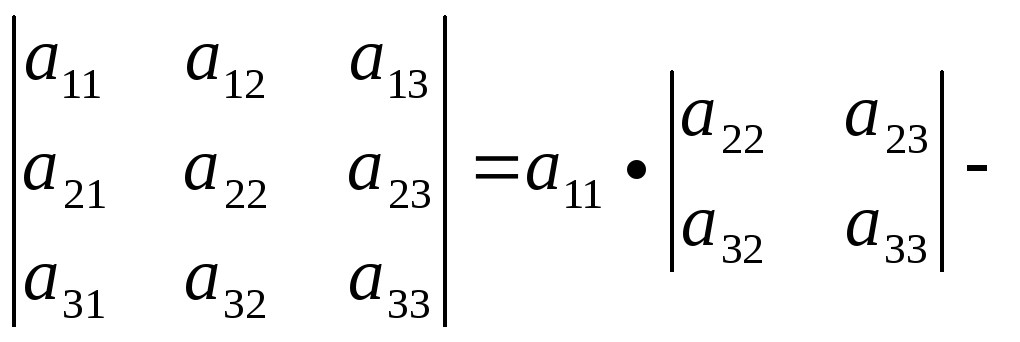
Последнюю формулу можно использовать как основную при вычислении определителя третьего порядка.
Теорема разложения позволяет свести вычисление определителя третьего порядка к вычислению трех определителей второго порядка.
Рекомендуется раскладывать определитель по той строке или столбцу, где есть нули, т.к. для нулевых элементов не надо находить алгебраические дополнения.
Теорема разложения дает второй способ вычисления определителей третьего порядка.
16. Понятие обратной матрицы.
Обра́тная
ма́трица —
такая матрица
A-1,
при умножении на которую исходная
матрица A
даёт в результате единичную
матрицу
E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её пределитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы
-
,
где det
обозначает
определитель. -
(AB) − 1 = B − 1A − 1 для любых двух обратимых матриц A и B.
-
(AT) − 1 = (A − 1)T где * T обозначает транспонированную матрицу.
-
(kA) − 1 = k − 1A − 1 для любого коэффициента
. -
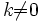Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A - 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
17. Метод обратной матрицы решения систем линейных уравнений.
Дана
система из трех уравнений с тремя
неизвестными. Установить, что система
уравнений имеет единственное решение
и найти его с помощью обратной
матрицы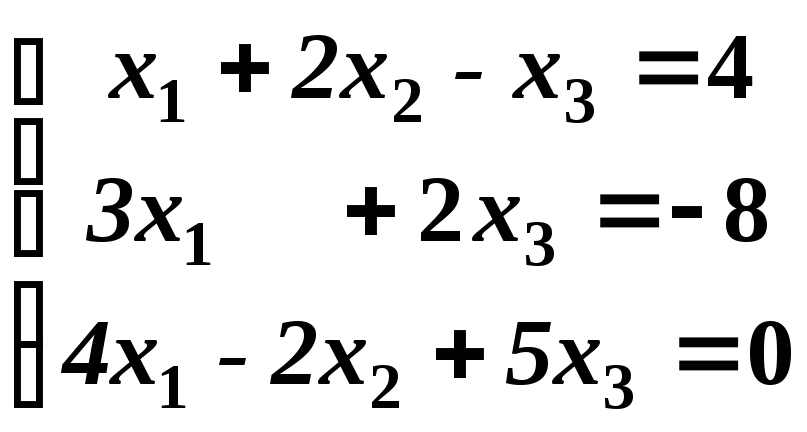
.
Решение.
Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).
Вычислим определитель данной системы :
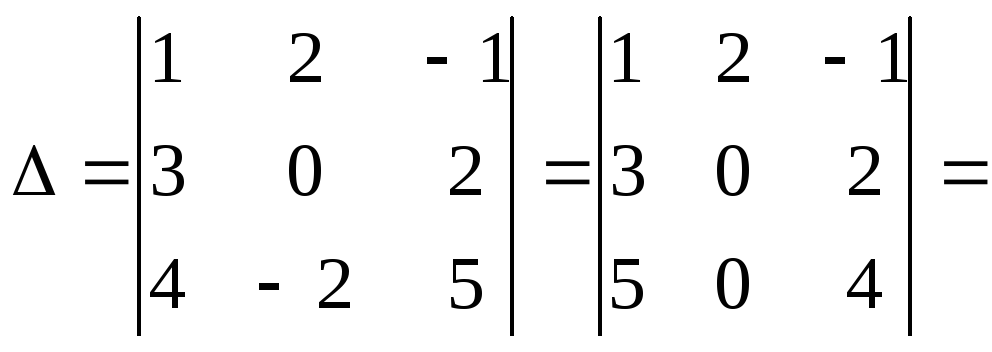
следовательно,
система имеет единственное решение.
Данную
систему можно записать в матричной
форме :
,
где
,
,
.
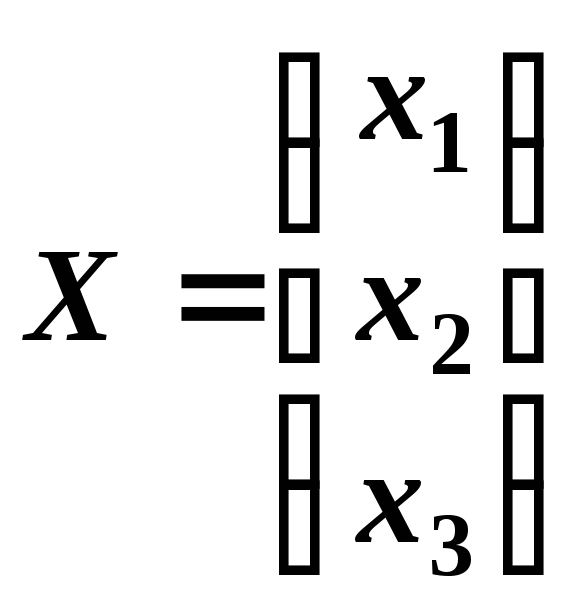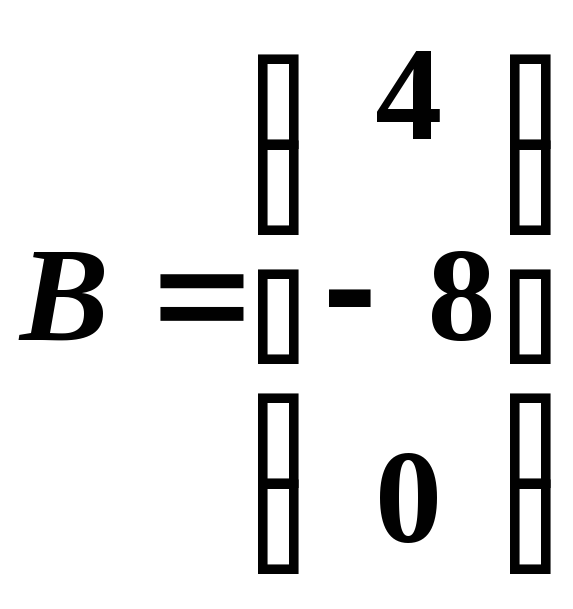Так
как
, то для матрицы
существует обратная матрица
.
Умножив матричное уравнение
слева на
,
получим
, откуда
,
или
.
Найдем
обратную матрицу
по формуле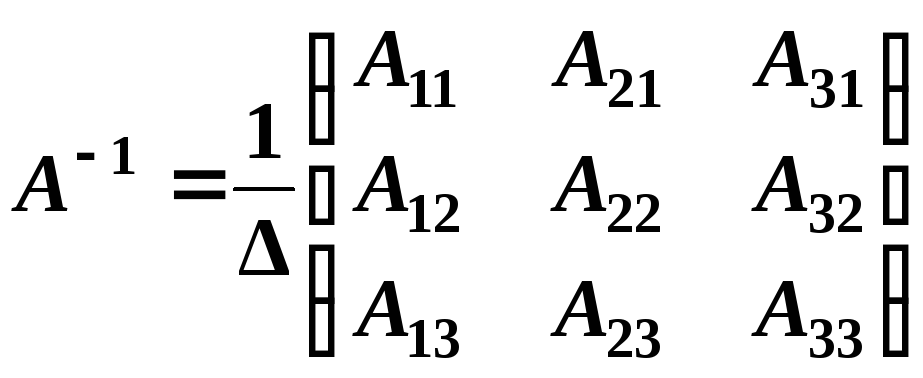
где
алгебраическое дополнение элемента
.
.
.
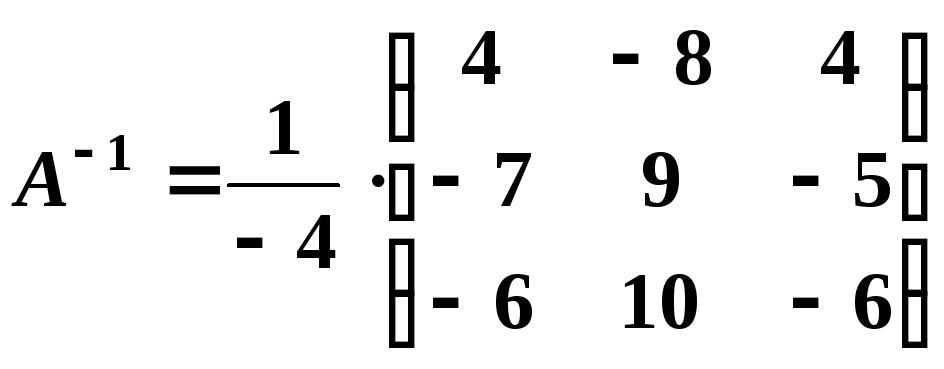Тогда
.
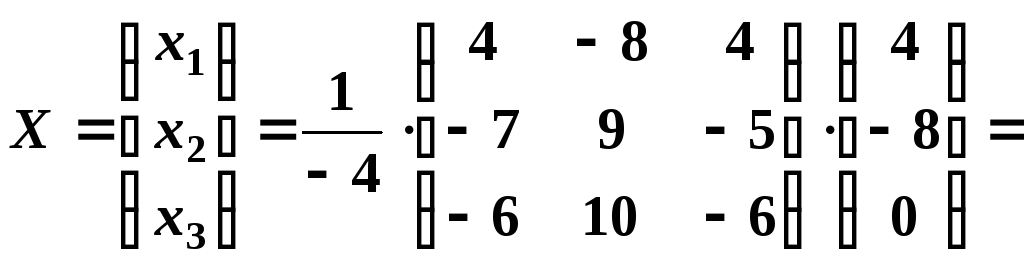
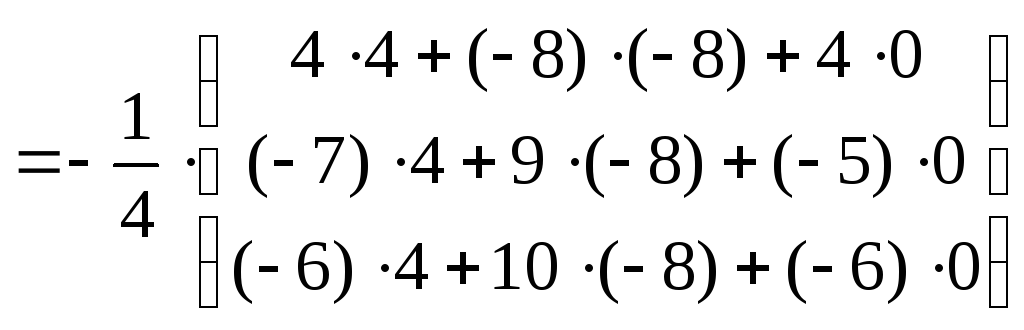
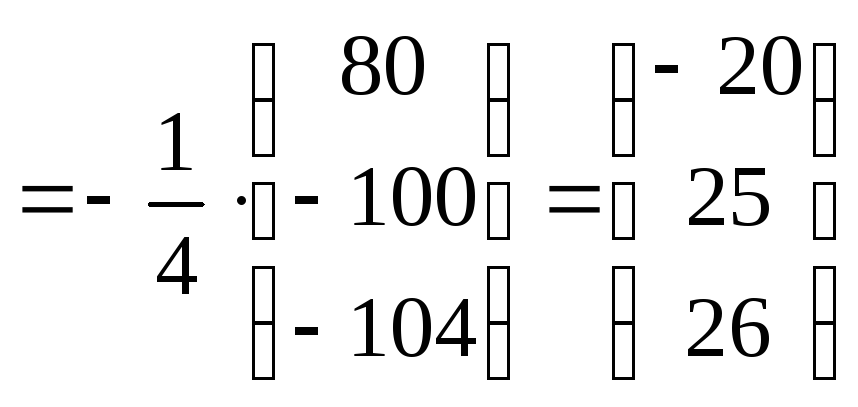Ответ
:
.
13 . Правило Крамера решения систем линейных уравнений.
Методом
Крамера
найти решение системы линейных
алгебраических уравнений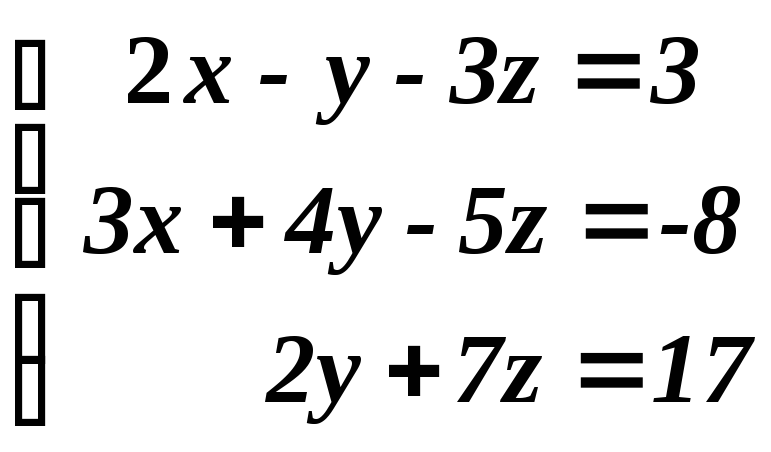
.
Решение.
Решение системы находим по формулам Крамера
Вычислим
определитель системы
.
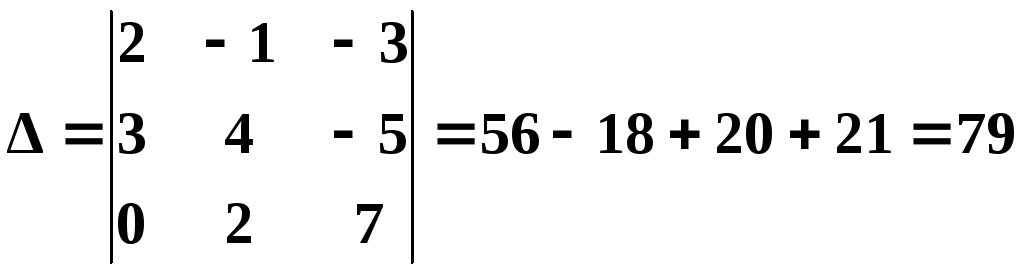
Последовательно
заменив в
,
первый, второй и третий столбцы столбцом
свободных членов, получим соответственно
.
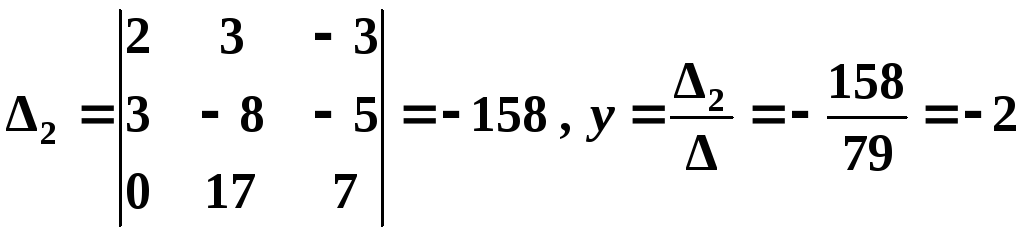
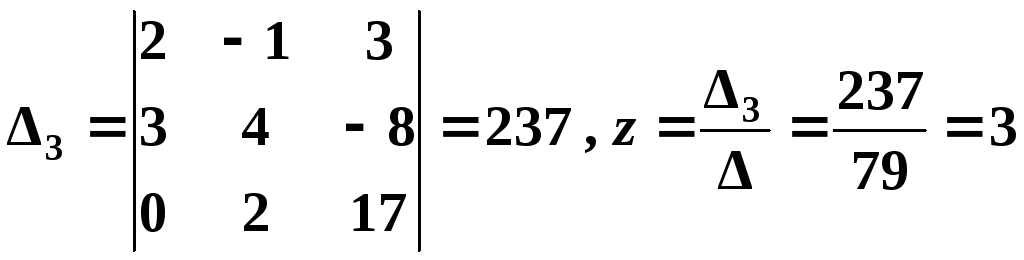Ответ
:
.
19. Понятие ранга матрицы. Его нахождение.
Пусть задана любая матрица А с m строк и n столбцов.
Рангом системы строк (столбцов) матрицы А называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Ранг матрицы равен наибольшему числу линейно независимых строк (или столбцов) матрицы.
Алгоритм
Искать ранг можно с помощью модифицированного метода Гаусса. Будем выполнять абсолютно те же самые операции, что и при решении системы или нахождении её определителя, но если на каком-либо шаге в i-ом столбце среди невыбранных до этого строк нет ненулевых, то мы этот шаг пропускаем, а ранг уменьшаем на единицу (изначально ранг полагаем равным max(N,M)). Иначе, если мы нашли на i-ом шаге строку с ненулевым элементом в i-ом столбце, то помечаем эту строку как выбранную, и выполняем обычные операции отнимания этой строки от остальных.