39Применение дифференциала для приближенных вычислений.

Пусть нам известно значение функции y₀=f(x₀) и ее производной y₀' = f '(x₀) в точке x₀. Покажем, как найти значение функции в некоторой близкой точке x.

Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x₀)·Δx.

Т.к., по определению, Δy = f(x) – f(x₀), то f(x) – f(x₀)≈f'(x₀)·Δx.

Откуда f(x) ≈ f(x₀) + f'(x₀)·Δx

Примеры.

1. y = x² – 2x. Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.

Имеем Δy≈dy=f'(x)·Δx.

f'(x)=2x – 2 ,f'(3)=4, Δx=0,01.

Поэтому Δy ≈ 4·0,01 = 0,04.

2. Вычислить приближенно значение функции 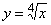в точке x = 17.

Пусть x₀= 16. Тогда Δx = x – x₀= 17 – 16 = 1, ,

.

Таким образом, .

3. Вычислить ln 0,99.

Будем рассматривать это значение как частное значение функции y=lnx при х=0,99.

Положим x₀ = 1. Тогда Δx = – 0,01, f(x₀)=0.

, f '(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = – 0,01.

56. Теорема Ферма.

Если функция имеет локальный экстремум в точке и производная существует, то .

Доказательство: Предположим для определенности, что — локальный максимум.

Тогда при всех , достаточно близких к . Следовательно, при всех , достаточно близких к нулю. Имеем, с одной стороны,

потому что числитель и знаменатель оба неотрицательны. С другой стороны,

потому что здесь и числитель, и знаменатель неположительны. Следовательно, .

Упражнение. Провести доказательство Теоремы Ферма для случая, когда имеет локальный минимум в точке .

Следующие два примера показывают, что для нахождения локальных экстремумов недостаточно найти точки, в которых производная обращается в нуль.

Пример 1. . Имеем , откуда , но, на самом деле, в нуле функция экстремума не имеет.

Пример 2. имеет локальный минимум в нуле, хотя не существует.

Определение. Пусть точка принадлежит области определения функции . Точка называется критической точкой функции , если производная равна нулю или не существует.

Пример 3. Найти критические точки функции .

Решение: используя правило произведения, нетрудно найти, что 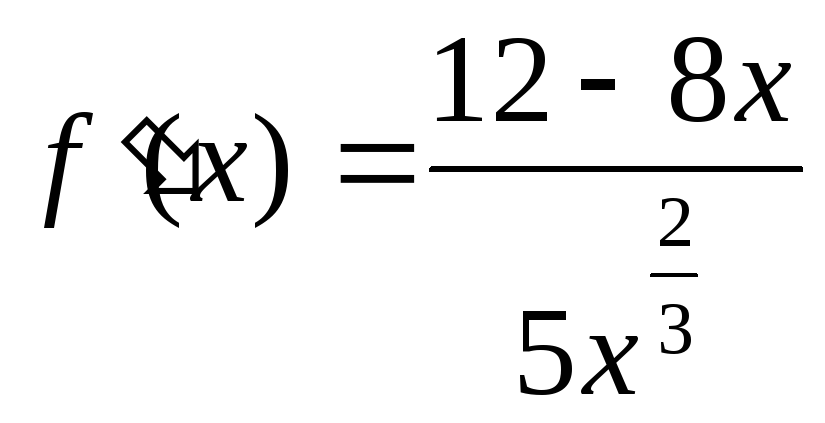, откуда находим две критические точки и .

Теперь теорему Ферма можно переформулировать более кратко.

Теорема (теорема Ферма в терминах критических точек). Функция может иметь

локальные экстремумы только в ее критических точках.

41Теорема Ролля.

(теорема о нуле производной) утверждает, что

Если функция, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Геометрический смысл:Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.