4.3. Декодирование кодов pc

Алгоритмы декодирования кодов PC весьма близки к алгоритмам для двоичных БЧХ кодов. Существенное различие относится только к вычислению v < t_d значений ошибок , 1 < ℓ < v. В общем случае это делается с помощью алгоритма Форни [For2]. Ниже представлено выражение, справедливое для кодов PC с произвольным множеством 2t_d последовательных нулей {a^b,a^b+l,…,а^b+δ},δ = 2t_d- 1,

(4.4)

где σ’(х) есть формальная производная по х многочлена локаторов ошибок σ(х) Многочлен Λ(х) в (4.4) это многочлен значений ошибок, определяемый как

(4.5)

Перед изучением первого примера декодирования кода PC мы рассмотрим другой вариант алгоритма БМ, известный как алгоритм Мэсси (или МА). Этот алгоритм был предложен Дж. Мэсси в [Mas2].

Алгоритм Мэсси синтеза ЛРОС

1. Начальные условия: многочлен обратной связи ЛРОС σ(х) = 1, корректор ρ(х) = х, счетчик i = 1, длина регистра ℓ = 0.

2. Взять следующий синдром и вычислить различие:

3. Проверить различие d: если d=0, то перейти к п. 8.

4. Модифицировать многочлен обратной связи:

5. Проверить длину регистра: если ℓ > i, то перейти к п. 7.

6. Исправить длину регистра и заменить корректор: положить ℓ=i- ℓ и ρ(х)= σ(х)/d.

7. Обновить многочлен обратной связи: σ(х)= σ_new(х).

8. Обновить корректор: ρ(х) = х ρ(х).

9. Обновить счетчик: i = i + 1.

10. Условие остановки: если i < d, то перейти к п. 2, иначе Стоп.

Пример 41. Пусть С код PC (7,3,5) из Примера 40. Положим, что многочлен

получен из канала связи. Тогда S₁ =r(1) = α + α ⁵ = α ⁶, S₂ = r(α) = α ³ + α ² = α ⁵, S₃ = r(α ²) = α ⁵ + α ⁶ = α и S₄ = r(α ³) = 1 + α ³ = α. Уравнение (3.16) получаем в виде:

Ниже рассмотрены три способа решения последнего уравнения.

Прямое решение (PGZ алгоритм)

Предположим, что произошли две ошибки. Тогда ∆₂ = α ⁷ + α ¹⁰ = 1 + α ³ = α≠0. Следовательно, должны были произойти две ошибки и

откуда следует, что

Алгоритм Мэсси

S₁ = α⁶, S₂ = α⁵, S₃ = α, S₄ = α

i = 0: σ(x)=1, ℓ=0, ρ(x)=x

i = 1: σ(x)=1, ℓ=0, ρ(x)=x

σ_new(x)=σ(x) +dρ(x)=1+α⁶x, 2l=0<i, ℓ= i - ℓ=1,

ρ(x)= σ(x)/d= α^-6= α,

ρ(x)= x ρ(x)= αx, σ(x) = σ_new(x).

i=2: d=S₂ +, ρ(x)= x ρ(x)= αx²

=

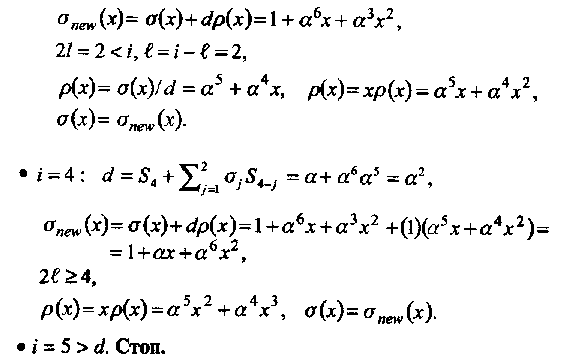
Евклидов алгоритм

• Начальные условия:

Алгоритм останавливается, так как deg[r₃(x)] = 2 = t_d. Следовательно, σ(х) = α³ + α⁴х +α²х² = α³(1 + αх + α⁶х²).

Все рассмотренные алгоритмы дали одинаковое, с точностью до константного множителя, решение для многочлена локаторов ошибок:

Таким образом, ошибки произошли на позициях j₁ = 2 и j₂ = 4. Координаты ошибок находятся с помощью процедуры Ченя как обратные величины корней многочлена локаторов ошибок σ(х). Заметим, что σ’(х) = 0, так как в поле GF(2^m) характеристики 2 справедливо равенство 2а = а+а=0.

Для вычисления значений ошибок (любым из рассмотренных алгоритмов) необходим многочлен значений ошибок (4.5),

Важно отметить, что алгоритм Евклида вычисляет σ(х) и Λ(х) одновременно, как σ(х) = b_last (x) и Λ(х) = r_last(x) (см. раздел 3.5.4, ЕА). Для проверки этого утверждения заметим, что

Если локаторы ошибок известны, то значения ошибок, найденные из уравнения (4.4). равны

Таким образом, е(х) = αх² + α⁵x⁴ и декодированное слово равно

Исправлены две ошибки.

Заметим, что оба полинома, найденные алгоритмом Евклида, имеют одинаковый константный множитель β, т.е. алгоритм находит βσ(х) и βΛ(х) с некоторым множителем β GF(2^m). Тем не менее, оба полинома имеют те же самые корни, что и полиномы, вычисленные алгоритмами БМА или PGZ. В результате и значения ошибок совпадают.

В большинстве программ, моделирующих процедуры кодирования и декодирования PC кодов, используется следующий эквивалентный способ определения значений ошибок [LC]. Пусть

(4.6)

Тогда значения ошибок равны [Вег]

(4.7)

где 1 .

Еще одна альтернатива алгоритму Форни, для малых значений t_d , состоит в следующем способе вычисления значений ошибок. Значения ошибок связаны с синдромами S_i системой линейных уравнений:

(4.8)

где 1 .

Каждая vv подматрица, образованная (известными) членами α^{(b+i-1) jℓ} образуют матрицу Вандермонда. Если известно положение всех v ошибок, то любое подмножество v уравнений (4.8) может быть использовано для определения значений ошибок. Например, используя первые v синдромов, получаем следующую систему линейных уравнений,

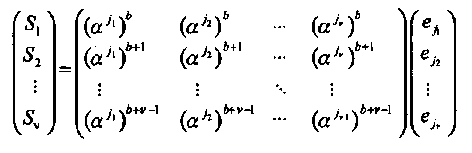(4.9)

решение которой может быть найдено над полем GF(2^m).

Пример 42. Рассмотрим тот же код PC и принятый многочлен из Примеров 40 и 41. Из (4.9) получаем

Определитель 2x2 матрицы равен ∆ = α⁴ + α ² = α. Отсюда следует, что

и

Полученные значения ошибок совпадают с теми, которые вычислены по алгоритму Форни. Подчеркнем еще раз, что этот способ может быть применен при исправлении только очень небольшого числа ошибок.