
- •Глава3 4
- •Часть 1 введение 4
- •Часть 2 коды хемминга, голея и рида-маллера 39
- •Часть 3 двоичные циклические коды и коды бчх 54
- •Часть 4 недвоичные бчх коды -коды рида-соломона 105
- •Глава3 часть 1 введение
- •1.1. Кодирование для исправления ошибок: Основные положения
- •1.1.1. Блоковые и сверточные коды
- •1.1.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •1.2. Линейные блоковые коды
- •1.2.1. Порождающая и проверочная матрицы
- •1.2.2. Вес как расстояние
- •1.3. Кодирование и декодирование линейных блоковых кодов
- •1.3.1. Кодирование с помощью матриц g и н
- •1.3.2. Декодирование по стандартной таблице
- •1.3.3. Хемминговы сферы, области декодирования и стандартная таблица
- •1.4. Распределение весов и вероятность ошибки
- •1.4.1. Распределение весов и вероятность необнаруженной ошибки в дск.
- •1.4.2. Границы вероятности ошибки в дск, каналах с абгш и с замираниями
- •1.5 Общая структура жесткого декодера для линейных кодов
- •Часть 2 коды хемминга, голея и рида-маллера
- •2.1. Коды Хемминга
- •2.1.1. Процедуры кодирования и декодирования
- •2.2. Двоичный код Голея
- •2.2.1 Кодирование
- •2.2.2. Декодирование
- •2.2.3. Арифметическое декодирование расширенного (24,12,8) кода Голея.
- •2.3. Двоичные коды Рида-Маллера
- •2.3.1. Булевы полиномы и рм коды
- •2.3.2. Конечные геометрии и мажоритарное декодирование.
- •Часть 3 двоичные циклические коды и коды бчх
- •3.1. Двоичные циклические коды.
- •3.1.1. Порождающий и проверочный полиномы.
- •3.1.2. Порождающий многочлен
- •3.1.3. Кодирование и декодирование двоичных циклических кодов.
- •3.1.4. Проверочный полином.
- •3.1.5. Укороченные циклические коды и crc коды
- •3.2. Общий алгоритм декодирования циклических кодов
- •3.1.5 Пакеты ошибок
- •3.2.1. Арифметика gf(q)
- •3.3. Двоичные коды бчх
- •3.4. Полиномиальные коды
- •3.5. Декодирование двоичных бчх кодов
- •2. Евклидов алгоритм (еа)
- •3.5.1. Общий метод декодирования для бчх кодов
- •3.5.2. Алгоритм Берлекемпа-Мэсси (вма)
- •3.5.3. Декодер pgz
- •3.5.4. Евклидов алгоритм (еа)
- •3.5.5. Метод Ченя и исправление ошибок
- •3.5.6. Исправление стираний и ошибок
- •3.6. Распределение весов и границы вероятности ошибки
- •3.6.1. Оценка вероятности ошибки
- •Часть 4 недвоичные бчх коды -коды рида-соломона
- •4.1. Коды pc как полиномиальные коды
- •4.2. От двоичных кодов бчх к pc кодам
- •4.3. Декодирование кодов pc
- •4.3.1. Комментарий к алгоритмам декодирования
- •4.3.2. Исправление ошибок и стираний
- •4.4. Распределение весов
- •Глоссарий
- •Литература
3.5.2. Алгоритм Берлекемпа-Мэсси (вма)
Алгоритм Берлекемпа-Мэсси лучше всего рассматривать как итеративный процесс построения минимального линейного

Рис. 23. ЛРОС с отводами σ1, σ 2,..., σ v и выходом S1, S2,..., S2v.
регистра (сдвига) с обратной связью (ЛРОС), аналогичного показанному на Рисунке 23, который генерирует известную последовательность синдромов S1 S2,...S2td.
Целью ВМА является построение многочлена (обратной связи) σ (i+1)(х) наименьшей степени, удовлетворяющего следующему уравнению, выведенному из (3.16):
![]() (3.18)
(3.18)
Решение этой задачи эквивалентно условию, что многочлен
![]()
является многочленом обратной связи ЛРОС, который генерирует ограниченную последовательность синдромов.
Несовместность (рассогласование, расхождение, различие) на i-ой итерации, определенная как
![]()
является мерой соответствия синдромной последовательности и генерируемой ЛРОС и содержит корректирующий множитель для вычисления σ (i+1) на следующей итерации. Возможны два случая:
![]() (3.19)
(3.19)
• Если di = 0, то уравнение (3.18) удовлетворяется с равенством
• Если di ≠ 0, то решение на следующей итерации имеет вид
![]() (3.20)
(3.20)
где является
решением на m-ой
итерации такое, что —1 < т≤
1,
![]() максимальна.
максимальна.
Итеративное
вычисление σ(i+1)(.х)
продолжается, пока не удовлетворятся
одно или оба условия: либо i
≥
![]() i+1,+td-1
либо i
= 2td-
1.
i+1,+td-1
либо i
= 2td-
1.
Начальными условиями алгоритма являются:
![]() (3.21)
(3.21)
Заметим также, что в Алгоритме Берлекэмпа-Мэсси используются программные инструкции (если — то). По этой причине ВМА не слишком удобен для аппаратной реализации. Тем не менее, по числу операций в конечном поле GF(2W) этот алгоритм весьма эффективен.
Пример 34. Пусть С двоичный (15,5,7) код БЧХ, исправляющий три ошибки из Примера 33. Для проверки вычислений и просто для справки приводится степенное и векторное представление элементов поля GF(16), порожденное примитивным многочленом р(х) = 1 + х + х4:
Таблица элементов поля GF(24), р(х) = 1 + х + х4:

Порождающий
многочлен кода С равен g(x) = х10
+ х8
+ х5
+ х4
+ х2
+ х + 1 . Предположим, что информационный
полином равен u(х)
= х + х2
+ х4
. Тогда соответствующее ему кодовое
слово равно![]()
Пусть принятое слово равно r(x) = 1+х + х2+х3 + х4 + х6 + х8 + х11 + x14, соответствующее вектору r(х) =v(х)+e(х), полученному в результате передачи слова v по ДСК. (Вектору е соответствует многочлен ошибок е(х) = 1 + х6 + х12. Хотя декодеру этот вектор ошибок неизвестен, он используется здесь для упрощения вычисления синдромов.)
Синдромы равны:

Алгоритм Берлекемпа-Мэсси (ВМА):
• Итерация 0: Инициализация.
![]()
• Итерация 1:
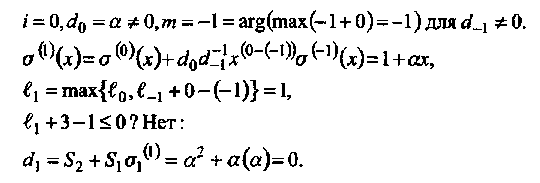
• Итерация 2:

• Итерация 3:

• Итерация 4:

• Итерация 5:

• Итерация 6:

Таким образом,![]()
То, что на нечетных шагах алгоритма di= 0 в предыдущем примере не случайность. Для двоичных кодов БЧХ это закономерность. С тем же результатом можно было выполнять только четные шаги алгоритма. Единственное изменение состоит в замене правила остановки на следующее
![]()
В результате снижается сложность декодирования. Читателю предлагается найти σ(х) в Примере 34, используя только три итерации.
