1.1. Кодирование для исправления ошибок: Основные положения

Все коды, исправляющие ошибки, основаны на одной общей идее: для исправления ошибок, которые могут возникнуть в процессе передачи или хранения информации, к ней добавляется некоторая избыточность. По основной схеме (используемой на практике), избыточные символы дописываются вслед за информационными, образуя кодовую последовательность или кодовое слово (codeword). В качестве иллюстрации на Рисунке 2 показано кодовое слово, сформированное процедурой

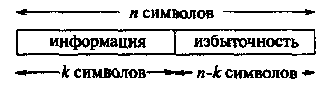
Рис. 2. Систематическое блоковое кодирование для исправления ошибок.

кодирования блокового кода (block code). Такое кодирование называют систематическим (systematic). Это означает, что информационные символы всегда появляются на первых к позициях кодового слова. Символы на оставшихся п-к позициях являются различными функциями от информационных символов, обеспечивая тем самым избыточность, необходимую для обнаружения или исправления ошибок. Множество всех кодовых последовательностей называют кодом, исправляющим ошибки (error correcting code), и обозначают через С.

1.1.1. Блоковые и сверточные коды

В соответствии с тем, как вводится избыточность в сообщение, коды, исправляющие ошибки, могут быть разделены на два класса: блоковые и сверточные (convolutional code) коды. Обе схемы кодирования нашли практическое применение. Исторически сверточные коды имели преимущество главным образом потому, что для них известен алгоритм декодирования Витерби с мягким решением и в течение многих лет существовала убежденность в том, что блоковые коды невозможно декодировать с мягким решением. Однако последние достижения в теории и конструировании алгоритмов декодирования с мягким решением для линейных блоковых кодов помогли рассеять это убеждение. Более того, наилучшие ЕСС, известные сегодня (в начале двадцать первого века), являются блоковыми кодами (нерегулярными кодами с низкой плотностью проверок - irregular low-density parity-check codes).

При блоковом кодировании каждый блок информационных символов обрабатывается независимо от других. Другими словами, блоковое кодирование является операцией без памяти в том смысле, что кодовые слова не зависят друг от друга. Выход сверточного кодера, напротив, зависит не только от информационных символов в данный момент, но и от предыдущих символов на его входе или выходе. Чтобы упростить объяснения, мы начнем с изучения структурных свойств блоковых кодов. Многие из этих свойств являются общими для обоих типов кодов.

Следует заметить, что на самом деле блоковые коды обладают памятью, если рассматривать кодирование как побитовый процесс в пределах кодового слова. Сегодня это различие между блоковыми и сверточными кодами кажется все менее и менее ясным, особенно после недавних достижений в понимании решетчатой (trellis) структуры блоковых кодов и кольцевой (tail-biting) структуры некоторых сверточных кодов.

Примечание: Название кольцевые сверточные коды еще не окончательно утвердилось в отечественной литературе, иногда tail-biting convolutional codes называют циклически замкнутыми.

Специалисты по сверточным кодам иногда рассматривают блоковые коды как «коды с меняющейся во времени структурой решетки» (time-varying trellis structure). Аналогично, специалисты в области блоковых кодов могут рассматривать сверточные коды как «коды с регулярной структурой решетки».