3.2. Общий алгоритм декодирования циклических кодов

Пусть r(х) = v(x) + e(x), где е(х) полином ошибок, ассоциированный с вектором ошибок ДСК. Тогда синдром (синдромный полином) имеет вид

s(x)= r(x) mod g(x)= e(x) mod g(x) (3.8)

На Рисунке 18 показана обобщенная структура декодера циклического кода. Синдром s(x) используется для определения полинома ошибок е(х). Так как циклический код является, прежде всего, линейным кодом, то эта структура может рассматриваться как вариант «стандартной таблицы» для циклических кодов.

Проблема декодирования равноценна поиску (неизвестного) полинома ошибок е(х) по известному синдрому s(x). Эти полиномы связаны уравнением (3.8), которое составляет основу синдромного декодера (известного также как декодер Меггита) для циклического кода. Другой (но близкий) вариант декодера, реализующий алгоритм ловли ошибок, известный также как декодер Касами, проверяет совпадение синдрома с возможным вектором ошибок. Только очень немногие классы

Рис. 18. Обобщенная структура декодера циклического кода.

кодов имеют такое относительно простое декодирование, как циклические коды Хемминга и Голея. Однако с увеличением корректирующей способности кода t = |_(d_min - 1)/2_| сложность декодера, основанного на комбинаторном обнаружении ошибок, становится чрезвычайно большой.

Предположим, что ошибка возникла на первой принятой позиции, т.е. е(х) = х^n-1 . Соответствующий синдром равен s(x) =x^n-1mod g(x). Если ошибка, искажающая заданную позицию, обнаруживается данным циклическим кодом, то могут быть обнаружены и ошибки на других позициях за счет циклических сдвигов и соответствующей коррекции синдрома. Синдромный декодер проверяет синдром для каждой позиции принятого слова и, если обнаруживается полином х^n-1 modg(x), то символ на этой позиции исправляется.

Пример 25. В этом примере рассматривается декодирование циклического (7,4,3) кода Хемминга с порождающим многочленом g(x) =x³+x+l. Схема вычисления синдрома показана на Рисунке 19. Принимаемые символы накапливаются в регистре сдвига и одновременно вводятся в схему деления на g(x). После приема седьмого бита содержимое этого регистра сдвигается на один разряд в каждом такте, а схема деления модифицирует синдром и проверяет совпадение с полиномом

Как только на выходе схемы проверки появится 1, будет исправлена ошибка в позиции х⁶. В тот же самый момент исправление вводится по обратной связи в схему деления и, тем самым, обнуляет остаток от деления. Нулевой остаток может рассматриваться как сигнал об успешном завершении декодирования. Проверка на нулевой остаток схемы деления позволяет обнаруживать некоторые аномалии по окончании процедуры декодирования.

Такт	s0	s1	s2	Ошибочная компонента
0	1	1	1	r5
1	1	0	1	r6
2	1	0	0	r0
3	0	1	0	r1
4	0	0	1	r2
5	1	1	0	r3
6	0	1	1	r4

Перейдем теперь к изучению циклических кодов, исправляющих многократные ошибки, для которых задача декодирования может рассматриваться как решение системы уравнений. По этой причине здесь необходимо знакомство с полем, в котором будут выполняться операции умножения, сложения

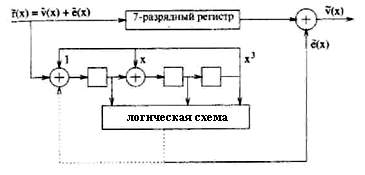
Рис. 19. Синдромный декодер двоичного циклического (7,4,3) кода Хемминга.

и деления. Циклические коды имеют хорошую алгебраическую структуру. Позднее будет показано, что эффективная реализация мощных алгоритмов декодирования достигается при использовании арифметики конечного поля, когда известно размещение корней порождающего многочлена кода.

Напомним, что порождающий полином всегда может быть представлен произведением двоичных неприводимых многочленов:

Алгебраическая структура циклических кодов выражается, в частности, в возможности определения корней каждого из многочленов в некотором поле разложения (которое является расширением поля, которому принадлежат коэффициенты многочлена). В интересующем нас случае поле разложения неприводимого многочлена является полем Галуа. В литературе поля Галуа называют также конечными полями, имея в виду конечное число принадлежащих ему элементов. Стандартным обозначением является GF(q), где q число элементов поля.

В общем случае число элементов поля есть степень простого числа, однако ниже будут рассматриваться только поля характеристики 2, когда q = 2^m.

Пример 26. В этом примере мы напомним читателям, что они хорошо знакомы с понятием «поле разложения». Рассмотрим поле действительных чисел. Известно, что в этом поле многочлен х² + 1 неприводим. Однако в поле комплексных чисел он раскладывается в произведение (х + i)(x –i ), где i = . Таким образом, комплексное поле является полем разложения (т.е. расширением) поля вещественных чисел.