Из условия прочности находим искомый диаметр

и ,

oткуда .

Удлинение участка CD находим по общей формуле

.

Здесь – это площадь трапеции mnrs, которая равна

.

Следовательно, .

Пример 14.

Стержень переменного сечения с соотношением площадей поперечных сечений A₁/A₂ =2 находится под действием сосредоточенных сил и собственного веса (рис. а). Материал стержня на всех участках одинаков. Требуется построить эпюры распределения продольной силы и напряжений вдоль оси стержня и определить перемещение сечения а–а.

Решение.

Строим эпюры изменения продольной силы и напряжений вдоль оси стержня. Собственный вес стержня принято учитывать, заменяя его распределенной по всей длине нагрузкой. Интенсивность распределенной нагрузки равна собственному весу, действующему на единицу длины стержня, т. е.

на первом и втором участках

,

на третьем участке

,

где – объемный вес материала стержня.

Эпюры продольной силы и напряжений строим, используя метод сечений. Заметим, что угол наклона эпюры продольной силы зависит от величины q и, следовательно, при построении эпюры N в масштабе угол ее наклона на первом и втором участке должен быть больше, чем на третьем участке, так как A₁ по условию больше, чем A₂ (рис. б). Угол же наклона эпюры напряжений зависит от объемного веса g, и поэтому угол наклона эпюры напряжений на всех участках одинаков (рис. в).

Находим перемещение (опускание) сечения а–а. Это перемещение можно искать разными способами. По первому способу для определения перемещения используем формулу . Здесь F – сосредоточенная сила, вызывающая перемещение участка длиной l; G – собственный вес рассматриваемого участка. Эту формулу можно использовать на участках постоянного сечения между сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т.е. заделки. Например, в рассматриваемой задаче перемещение сечения а–а складывается из удлинения участка длиной l₁, которое мы обозначим , и удлинения участка длиной . При определении удлинения в формуле сила F равна сумме F₁, F₂ и собственного веса всех расположенных ниже участков. Вес участка стержня длиной l₁: . Таким образом, по формуле

.

Удлинение происходит под действием сосредоточенной силы, состоящей из силы F₂, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка . То есть

.

Окончательно опускание сечения а–а равно .

Если построена эпюра распределения напряжений, то для определения перемещения заданного сечения удобно использовать второй способ, применяя формулу . В этой формуле , а – это площадь эпюры напряжений. Таким образом, если найти площадь двух трапеций на участке между неподвижным сечением (заделкой) и сечением а–а (заштрихованные площади и эпюры на рис.  в) и разделить полученную величину на модуль упругости, мы получим искомое перемещение сечения а–а:

.

При вычислении перемещения обращайте внимание на единицы измерения величин, входящих в формулы. Рекомендуем окончательный результат получить в сантиметрах.

Пример 15.

Построить эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рис. а. Принять a = 0,4 м; площадь поперечного сечения бруса на участках III и IV А = 20 см²; сосредоточенная сила F = 0,5 кН, собственный вес = 0,0078 кг/см³ = 76,44 кН/м³.

Решение.

Для определения внутренних усилий разбиваем брус с прямолинейной осью на четыре участка. Проводим сечение I – I (рис. а) и отбрасываем верхнюю часть бруса, заменяя действие отброшенной части нормальной силой N₁ (рис. б). Так как сечение I –I может быть проведено в любом месте участка I, то длина оставшейся части участка будет переменной величиной, и поэтому обозначим ее через x (рис. б), причем . Запишем уравнение равновесия, проектируя силы, действующие на оставшуюся часть бруса, на направление оси бруса:

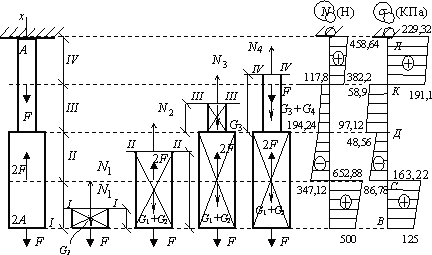
а б в г д е ж

откуда

Через обозначен собственный вес оставшейся части бруса первого участка, в пределах которого площадь поперечного сечения равна 2А, а длина оставшейся части обозначена через x. Подставим численные значения в полученную формулу:

.

Записанное выражение показывает, что эпюра нормальных сил в пределах первого участка представляет собой наклонную прямую линию. Для построения этой прямой определим значение нормальной силы N₁ в начале первого участка (x = 0): N₁(x = 0) = 500 Н и в конце первого участка (x = a= 0,5 м): N₁ (х = 0,5 м) =

Полученные значения откладываем в масштабе в соответствующих точках эпюры нормальных сил (рис. е). Найденные точки соединяем прямой линией, затем штрихуем первый участок эпюры прямыми линиями, перпендикулярными к оси бруса.

Проводим сечение II – II и повторяем порядок расчета, описанный выше для сечения I – I. Переменная величина х участка II – II будет изменяться в пределах . Составим уравнение равновесия (рис. в)

откуда

где – собственный вес части бруса, расположенного ниже сечения II – II.

Окончательно имеем

Определяем значение нормальной силы N₂ в начале второго участка (х= 0,5 м):

и в конце этого же участка (х = х_max = 1 м):

Полученные значения N₂ откладываем в масштабе в начале и в конце второго участка (рис. е).

Проводим сечение III – III и для оставшейся части бруса составляем уравнение равновесия (рис. г)

откуда где – собственный вес оставшейся части бруса третьего участка; – собственный вес первого и второго участков.

Тогда для участка

где нормальная сила N₃ в начале третьего участка будет N₃(х=0) = –194,2 Н; а в конце третьего участка получаем N₃ (х = a = 0,5 м) = –117,8 Н. Найденные значения N₃ переносим на эпюру нормальных сил.

И наконец, рассматривая равновесие оставшейся части бруса, после проведения сечения IV – IV получаем (рис. д)

откуда где Н – собственный вес участков I – I и II – II, – собственный вес третьего и оставшейся части четвертого участков.

В этом случае имеем

т.е. в начале четвертого участка N₄ (х = 0,5 м) = 382,2 Н, а в конце этого же участка N₄ (х = 1 м) = 458,64 Н. Вычисленные значения N₄ откладываем в масштабе на эпюре нормальных сил (рис. е).

Эпюра нормальных сил показывает, что первый и четвертый участок подвержены растяжению, а второй и третий – сжатию.

Для вычисления значений нормальных напряжений и построения эпюры нормальных напряжений используем формулу:

Эпюра нормальных напряжений показывает, что самое большое нормальное напряжение возникает в сечении, проходящем через точку Л четвертого участка (рис. ж), т.е. на опоре.

Перемещения поперечных сечений брусьев в статически определимых задачах при растяжении-сжатии

Пример 16.

Определить перемещение нижнего конца стержня, изображенного на рис. а. Задачу решить без учета собственного веса материала бруса. Принять a = 0,5 м; А = 10 см²; сосредоточенная сила F = 10 кН.

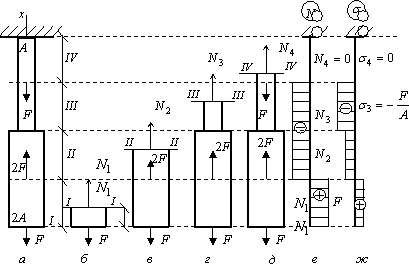
Решение. Для рассматриваемого случая эпюра нормальных сил представлена на рис. е. Для стержня со ступенчатым изменением площади и нормальных сил перемещения поперечных сечений вычисляются по формуле (1.7). Рассматривая рис. а и рис. е, запишем формулу для определения перемещения нижнего конца стержня в виде:

Знак «минус» в ответе показывает, что общая длина стержня уменьшится, т.е. нижний конец стержня переместится вверх вдоль его оси на величину мм.

Пример 17.

Определить перемещение нижнего конца стержня, изображенного на рис. а. Принятьобъемный вес материала стержня = 76440 Н/м³.

Решение.

Для рассматриваемого случая эпюра нормальных сил представлена на рис. б.

Эпюра нормальных сил построена с учетом сосредоточенных внешних сил и с учетом собственного веса материала бруса. Выделим на эпюре нормальных сил (рис. б) ее постоянные нормальные составляющие и треугольные участки эпюры, учитывающие собственный вес соответствующего участка. Разделение составляющих эпюры нормальных сил на рис. б произведено пунктирными линиями.

Теперь перемещение поперечного сечения от постоянной составляющей эпюры нормальных сил будет определяться по формуле а перемещение от действия собственного веса – по формуле

Для рассматриваемого случая формула для определения перемещения нижнего конца стержня будет иметь вид

Знак «+» показывает, что общая длина стержня увеличится, т.е. нижний конец стержня переместится вниз вдоль его оси на величину м (рис. а).

Определим перемещение сечения а – а (рис. а). Для этого мысленно разрежем эпюру нормальных сил в соответствующем сечении а – а и отбросим нижнюю часть эпюры. На основании оставшейся части эпюры нормальных сил (рис. в) определяем перемещение сечения а – а, используя формулы и

Полученный ответ показывает, что поперечное сечение а – а переместится вниз вдоль оси стержня.

Пример 18.

Для стального бруса квадратного сечения сжатого силой Р с учетом собственного веса при исходных данных приведенных ниже, требу­ется (см. рис. а):

1. Определить количество расчетных участков;

2. Составить аналитические выражения для нормальных сил N_z , нормальных напряжений и вычислить их значения для каж­дого из участков с учетом их собственных весов;

3. Построить эпюры N_z и ;

4. Вычислить перемещение верхнего конца колонны от дейст­вия силы Р и собственного веса.

Дано: Р = 20 кН; l₁ = l₂ = l₃ = 0,4 м; модуль упругости стали Е =  кН/м²; F₁ =  м²; F₂ =  м²; F₃ =  м²;  = 78 кН/м³ .

Решение.

1. Определение количества участков. Так как нор­мальная сила N_z зависит от величин внешних сил, в данном случае включающих в себя и собственный вес колонны, а последний, в свою очередь, от размеров попе­речного сечения F_i и объемного веса g, то границами участков следует назначать те сечения, в которых приложены внешние сосредоточенные силы и где происходит скачкообразное изменение площади попе­речного сечения или объемного веса материалов конструкций.

Исходя из вышесказанного, учитывая =const, брус будет иметь три участка:

1 участок - от 0 до сечения В (где приложена сила Р);

2 участок - от сечения В до сечения С;

3 участок - от сечения С до сечения D.

Следует заметить, что при определении нормальных напряже­ний используются те же участки.

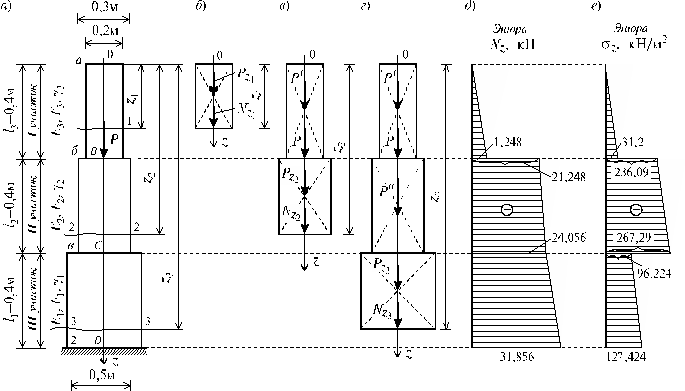
2. Составить аналитические выражения для нор­мальных сил N_z, нормальных напряжений s_z и вычис­лить их значения для каждого из участков, с учетом их собственных весов. Для этого воспользуемся методом сече­ний.

1 участок (0 - В) .

Проведя сечение 1 - 1 на расстоянии z₁ от начала координат (точка 0), рассмотрим равновесие верхней части. При этом, к рас­сматриваемой части прикладываются в центре ее тяжести собствен­ный вес и нормальная сила , заменяющую действие отброшен­ной нижней части бруса на верхнюю рассматриваемую (рис. б). Составив уравнение равновесия рассматриваемой верхней части ко­лонны по оси z , получим:

.

В свою очередь, собственный вес верхней части колонны оп­ределяется следующим образом:

 кН.

Тогда выражение для нормальной силы будет иметь вид:

 кН,

а для нормальных напряжений :

 кН/м2.

Так как, и линейно зависят от z₁ , то для построения их графиков (эпюр) достаточно определить значения этих величин на границах участка, т.е.

при z₁ = 0

при z₁ = 0,4 м кН;

кН/м².

Знаки минус при и указывают на то, что принятое на­правление для этих величин не совпадает с действительным, т. к. в принятой схеме продольная сила не растягивает, а сжимает первый участок.

2 участок (В - С) .

Аналогично предыдущему проводим сечение 2-2 на расстоянии z₂ (рис. в). Для верхней части составляем уравнение равновесия .

В это уравнение войдут: собственный вес первого участка ; собственный вес отсеченной части второго участка ; сосредоточенная сила Р = 20 кН, а также сила .

Тогда уравнение равновесия примет вид:

,

отсюда

= =  кН.

Учитывая постоянство площади поперечного сечения на втором участке, выражение для нормального напряжения может быть запи­сано таким образом:

кН/м².

Вычислим значения ординат и в граничных сечениях второго участка:

при z₂ = 0,4 м кН,

кН/м²;

при z₂ = 0,8 м кН,

кН/м².

3 участок (С - D) .

Составив уравнение равновесия (рис. г) для верхней части бруса, получим:

,

откуда

кН.

Выражение для напряжения:

кН/м².

Вычислим значения ординат и в граничных сечениях третьего участка:

при z₃ = 0,8 м (0,8) = -19,5 (0,8 + 0,43364) = -24,056 кН,

(0,8) = -78 (0,8 + 0,43364) = -96,224 кН/м²;

при z₃ = 1,2 м (1,2) = -19,5 (1,2 + 0,43364) = -31,856 кН,

кН/м².

3. Построение эпюр N_z и. По причине линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений N_z и в граничных сечениях каждого из участков (см. рис. д, е). Необходимым условием правильности построения этих графиков является выпол­нение следующих требований:

- скачок в эпюре N_z должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;

- скачки в эпюре должны совпадать с точками приложения внешней силы Р и изменения площади поперечного сечения ко­лонны.

После анализа полученных эпюр (рис. д, е) легко можно убедиться, что построения выполнены правильно.

4. Вычисление перемещения верхнего конца ко­лонны от действия всех сил. Полное перемещение со­гласно закону Гука может быть вычислено по формуле

.

В данном случае это выражение принимает следующий вид:

Так как величины определенных интегралов равны площадям, очерченным соответствующими подынтегральными функциями, то для вычисления перемещений достаточно вычислить площади эпюры N_z на каждом из этих участков и разделить их на E_i F_i . Следовательно,

.

Пример 19.

Найти закон изменения площадей поперечного сечения бруса равного сопротивления, испытывающего растяжение под действием силы и собственного веса.

Решение. В каждом сечении бруса равного сопротивления нормальные напряжения должны быть равны постоянной величине (). Запишем условие равновесия элемента длиной dx:

или

Имеем dG – собственный вес элемента бруса длиной dx:

тогда или

Интегрируя последнее выражение, находим

где С – произвольная постоянная интегрирования, которая находится из граничных условий. Окончательно запишем

Постоянную интегрирования находим из условия, что при х = 0 имеем А(х) = А₀, т.е. получаем .

Таким образом, закон изменения площади поперечного сечения А(х) получает вид

,

т.е. в брусе равного сопротивления площади поперечных сечений изменяются по логарифмическому закону.

Расчеты на растяжение и сжатие статически определимых стержневых систем

Пример 20.

Абсолютно жесткий брус ВС (Е_ВС = ) прикреплен в точке С к неподвижному шарниру (см. рис.), а в точке В поддерживается стальной тягой АВ. В точке В приложена вертикальная сила F = 20 кН.

Подобрать сечение тяги АВ и показать перемещение точки В. Расчетное сопротивление стали растяжению коэффициент условий работы а модуль упругости стали тяги АВ –

Решение.

Вырежем мысленно узел В (рис. б) и составим для него уравнения равновесия:

откуда находим

откуда

Окончательно имеем

Следовательно, брус ВС сжат силой N₂, а элемент АВ растянут силой N₁.

Подбор сечения тяги АВ проводим по формуле откуда определяем

Предположим, что тяга АВ имеет круглое поперечное сечение, тогда A_n = 1,44 см² = , откуда находим r = 0,677 см и d = 1,35 см.

Определим удлинения стержней АВ и СВ:

Таким образом, точка В переместится в точку В^/ по дуге окружности радиусом , причем расстояние между точками А и В^/ будет равно

Пример 21.

Определить из расчетов на прочность и жесткость допускаемую силу F, если [] = 120 МПа, [] = 1,7 мм, А₁ = 2А, А₂ = А = 5 см², l₁ = l₂ = l = 1 м, Е = 200 ГПа.

Р е ш е н и е.

1. Определение усилий в стержнях.

Из условия равновесия бруса АС имеем

, , ;

, , .

2. Расчет на прочность.

Находим напряжения в стержнях

,

.

Как видим, наиболее нагруженным является 2-й стержень, прочность которого предопределяет прочность всей конструкции в целом. Из условия прочности находим = 30 кН.

3. Расчет на жесткость.

Вычисляем деформации стержней

,

,

а по ним перемещение точки С. Из подобия треугольников В₁А₁В₂ и С₁А₁С₂ имеем:

В₁В₂/А₁В₂ = С₁С₂/А₁С₂ или ,

откуда .

Записываем условие жесткости ,

откуда = 200×10⁹×5×10^-4×1,7×10^-3/(8,5×1)= 20 кН.

Допускаемая нагрузка из расчета на жесткость получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.

кН.

Пример 22.

К двум одинаковым стержням приложена сила F. Установить, при каком угле конструкция будет иметь наименьший вес?

Р е ш е н и е.

Вес конструкции является функцией угла , т.е. .

Нам необходимо установить такой угол, при котором функция принимает минимальное значение. В теории оптимального проектирования она называется целевой функцией.

Для определения веса стержневой системы нужно знать площади сечений стержней. Из условия равновесия узла С находим усилия в стержнях:

, , ,

а из условия прочности – площади их поперечных сечений:

, откуда .

Учитывая, что длины стержней , находим вес конструкции (целевую функцию):

.

Функция принимает минимальное значение, когда

, откуда и .

Определение грузоподъемности статически определимой конструкции, работающей на растяжение-сжатие. Расчет по допускаемым напряжениям

При таком подходе несущая способность конструкции отождествляется с несущей способностью наиболее нагруженного элемента. Последовательность расчета при этом выглядит следующим образом.

Составляются уравнения статики и по числу лишних неизвестных – дополнительные уравнения совместности деформаций. Решая полученную систему, определяют усилия в стержнях и связанные с ними напряжения. Из сопоставления напряжений в наиболее нагруженном элементе с допустимой величиной делается заключение о надежности конструкции либо определяются искомые величины (размеры сечения стержней, допускаемая нагрузка).