
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
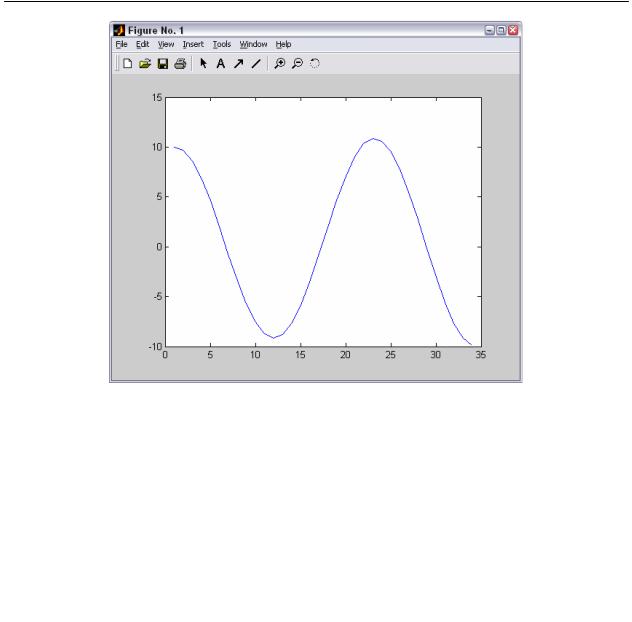
Риунок 14 - График функции, представляющей вектор Y с комплексными элементами.
Функция hist – построение графика гистограммы заданного вектора. Стандартное обращение имеет вид: hist(y,x), где y – вектор, гистограмму которого нужно построить; x – вектор, определяющий интервалы изменения первого вектора, внутри которых подсчитывается число элементов вектора y.
Многомерные данные.
MATLAB использует метод ориентации столбцов для многомерных статистических данных. Каждый столбец в наборе данных представляет переменную, а каждая строка - результаты наблюдений. Таким образом, элемент (i, j) - это i-oe наблюдение j-ой переменной.
В качестве примера рассмотрим набор данных с тремя переменными:
*частота сердечных сокращений
*вес
*часы упражнений за неделю
Для пяти наблюдений, результирующий массив может выглядеть следующим образом:
D= 72 134 3,2 81 201 3,5 69 156 7,1 82 168 2,4
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
37 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
75 170 1,2
Первая строка содержит частоту сердечных сокращений, вес и часы упражнений для первого пациента, вторая строка содержит аналогичные данные для второго и т.д. Вы можете применить многие функции MATLAB для анализа данных к этому набору информации.
Например, для того, чтобы получить среднее и среднеквадратичное отклонение для каждого столбца, надо
mu = mean(D) , sigma = std(D).
Для сортировки данных по столбцам служит функция sort.
Функция cov(A) вычисляет матрицу ковариаций измерений. При этом получается квадратная симметричная матрица с числом строк и столбцов, равным числу измеренных величин, т.е. числу столбцов матрицы измерений. На диагонали матрицы ковариаций размещены дисперсии измеренных величин, а вне её – взаимные корреляционные моменты этих величин.
Функция corrcoef(A) вычисляет матрицу коэффициентов корреляции при тех же условиях. Элементы этой матрицы связанны с элементами матрицы ковариаций следующим соотношением: C= cov(A), S= corrcoef(A),
|
C(k,l) |
S(k,l) = |
C(k, k)C(l,l) . |
1.2 Задание к лабораторной работе.
1.Создать ASCII файл с результатами двадцати измерений трёх случайных величин.
2.Загрузить созданный файл в рабочую область.
3.Просмотреть информацию о состоянии рабочей области.
4.Вычислить среднее и среднеквадратичное отклонение для каждого столбца.
5.Вычислить ковариационную и корреляционную матрицы для заданных случайных величин.
6.Построить гистограммы.
В ходе выполнения лабораторной работы могут понадобиться
дополнительные сведения о возможностях пакета. Эту информацию можно получить из [1] или из справочной системы самого пакета.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
38 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №2 Управление потоками. Создание М-файлов. Обработка массивов
данных.
Цель работы: освоить основные подходы работы с потоками и файлами в среде Matlab.
2.1 Краткие теоретические сведения
Понятие о файлах-сценариях и файлах-функциях
Здесь полезно отметить, что m-файлы, создаваемые редактором/отладчиком, делятся на два класса:
•файлы-сценарии, не имеющие входных параметров;
•файлы-функции, имеющие входные параметры.
Файл-сценарий, или Script-файл не имеет списка входных параметров и
является примером простой процедуры без параметров. Он использует глобальные переменные, т. е. такие переменные, значения которых могут. Для запуска файла-сценария из командной строки MATLAB достаточно указать его имя в этой строке.
Файл-функция отличается от файла-сценария прежде всего тем, что созданная им функция имеет входные параметры, список которых указывается в круглых скобках. Используемые в файле-функции переменные являются локальными переменными, изменение значений которых в теле функции никоим образом не влияет на значения, которые те же самые переменные могут иметь за пределами функции.
Иными словами, локальные переменные могут иметь те же имена (идентификаторы), что и глобальные переменные (хотя правила культурного программирования не рекомендуют смешивать имена локальных и глобальных переменных).
Основные понятия программирования
С позиций программиста язык программирования системы является типичным проблемно-ориентированным языком программирования высокого уровня. Точнее говоря, это даже язык сверхвысокого уровня, содержащий сложные операторы и функции, реализация которых на обычных языках (например, Бейсике, Паскале или Си) потребовала бы много усилий и времени. К таким функциям относятся матричные функции, функции быстрого преобразования Фурье (БПФ) и др., а к операторам — операторы построения разнообразных графиков, генерации матриц определенного вида и т. д.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
39 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Основные средства программирования
Итак, программами в системе MATLAB являются m-файлы текстового формата, содержащие запись программ в виде программных кодов. Язык программирования системы MATLAB имеет следующие средства:
•данные различного типа;
•константы и переменные;
•операторы, включая операторы математических выражений;
•встроенные команды и функции;
•функции пользователя;
•управляющие структуры;
•системные операторы и функции;
•средства расширения языка.
Коды программ в системе MATLAB пишутся на языке высокого
уровня, достаточно понятном для пользователей умеренной квалификации в области программирования. Язык программирования MATLAB является типичным интерпретатором. Это означает, что каждая инструкция программы распознается и тут же исполняется, что облегчает обеспечение диалогового режима общения с системой. Этап компиляции всех инструкций, т. е. полной программы, отсутствует. Высокая скорость выполнения программ обеспечена наличием заведомо откомпилированного ядра, хранящего в себе критичные к скорости выполнения инструкции, такие как базовые математические и иные функции, а также тщательной отработкой системы контроля синтаксиса программ в режиме интерпретации.
Основные типы данных
Структура типов данных системы MATLAB представлена ниже: Типы данных array и numeric являются виртуальными, поскольку к ним
нельзя отнести какие-либо переменные. Они служат для определения и комплектования некоторых типов данных. Таким образом, в MATLAB определены следующие основные типы данных, в общем случае представляющих собой многомерные массивы:
•single — числовые массивы с числами одинарной точности;
•double — числовые массивы с числами удвоенной точности;
•char — строчные массивы с элементами-символами;
•sparse — наследует свойства double, разреженные матрицы с элементами-числами удвоенной точности;
•сеll — массивы ячеек; ячейки, в свою очередь, тоже могут быть массивами;
•struct — массивы структур с полями, которые также могут содержать массивы;
•function_handle — дескрипторы функций:
•int32, uint32 — массивы 32-разрядных чисел со знаком и без знаков;
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
40 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
•intl6,uint!6 — массивы 16-разрядных целых чисел со знаком и без знаков;
•int8. uint8 — массивы 8-разрядных целых чисел со знаками и без знаков.
Кроме того, предусмотрен еще один тип данных — UserObject, который относится к типам данных (объектом), определяемым пользователем. Типы данных double, char и sparse были рассмотрены ранее, так что в этой главе будут детально рассмотрены оставшиеся типы. Что касается чисел класса uint8, то они представляют значения от 0 до 255 и занимают в памяти 1/8 часть от размера одного числа с двойной точностью. В основном этот тип данных применяется в служебных целях.
Каждому типу данных можно соотнести некоторые характерные для него операции, называемые методами. Дочерние типы данных, расположенные на приведенной диаграмме ниже родительских типов, наследуют от последних их методы, что является признаком наследования объектов. Поскольку в иерархии типов данных сверху находятся данные типа array, это значит, что все виды данных в MATLAB являются массивами.
Виды программирования
Язык программирования системы MATLAB вобрал в себя все средства, необходимые для реализации различных видов программирования:
•процедурного;
•операторного;
•функционального;
•логического;
•структурного (модульного);
•объектно-ориентированного;
•визуально-ориентированного.
Воснове процедурного, операторного и функционального типов программирования лежат процедуры, операторы и функции, используемые как основные объекты языка. Эти типы объектов присутствуют в MATLAB. Логическое программирование реализуется в MATLAB с помощью логических операторов и функций. Это позволяет реализовать основные идеи логического программирования, хотя на выдающуюся роль в этом классе языков программирования MATLAB не претендует.
Зато MATLAB представляет собой яркий пример плодотворности структурного программирования. Подавляющее большинство функций и команд языка представляют собой вполне законченные модули, обмен данными между которыми происходит через их входные параметры, хотя возможен обмен информацией и через глобальные переменные. Программные модули оформлены в виде текстовых m-файлов, которые хранятся на диске и подключаются к программам по мере необходимости. Важно отметить, что в отличие от многих языков программирования,
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
41 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
применение тех или иных модулей не требует предварительного объявления, а для создания и отладки самостоятельных модулей MATLAB имеет все необходимые средства. Подавляющее большинство команд и функций системы MATLAB поставляется в виде таких модулей.
Объектно-ориентированное программирование также широко представлено в системе MATLAB. Оно особенно актуально при программировании задач графики. Что качается визуально-ориентированного программирования, то в MATLAB оно представлено в основном в пакете моделирования заданных блоками устройств и систем Simulink. Этот пакет будет рассмотрен в конце книги. В ядре системы в данный момент визуально-ориентированное программирование не используется.
Двойственность операторов, команд и функций
Для языка системы MATLAB различие между командами (выполняемыми при вводе с клавиатуры) и программными операторами (выполняемыми из программы) является условным. И команды, и программные операторы могут выполняться как из программы, так и в режиме прямых вычислений. Под командами далее в основном понимаются средства, управляющие периферийным оборудованием, под операторами — средства, выполняющие операции с операндами (данными).
Функция преобразует одни данные в другие. Для многих функций характерен возврат значений в ответ на обращение к ним с указанием списка входных параметров — аргументов. Например, говорят, что функция sin(x) в ответ на обращение к ней возвращает значение синуса аргумента х. Поэтому функцию можно использовать в арифметических выражениях, например
2*sin(x+1 f_nаmе(Список_параметров).
Важное значение имеет двойственность операторов и функций. Многие операторы имеют свои аналоги в виде функций. Так, например, оператор «+» имеет аналог в виде функции sum. Команды, записанные в виде
Command argument
нередко имеют форму записи и в виде функции:
Command('argument')
Некоторые ограничения
Поскольку язык программирования системы MATLAB ориентирован на структурное программирование, в нем нет номеров строк (присущих до недавнего времени Бейсику) и программных операторов безусловного перехода GO TO. Имеются лишь управляющие структуры следующих типов:
условных выражений if... el se...elseif...end, циклы for...end и while...end. Их форма похожа на ту, которая используется в языке Pascal (т. е. область действия управляющих структур начинается их заголовком, но без слова begin, а заканчивается словом end). С позиций теории структурного
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
42 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
программирования этих средств достаточно для решения любых задач. В MATLAB имеются также операторы-переключатели типа case.
Однако в MATLAB исключены те средства, возможности которых можно реализовать уже имеющимися средствами. Зато резко увеличен набор средств программирования для решения математических задач, прежде всего сводящихся к матричным вычислениям и реализации современных численных методов.
М-файлы сценариев и функций
Структура и свойства файлов сценариев
Итак, мы установили, что работа в командном режиме (сессия) не является программированием. Внешним атрибутом последнего в MATLAB служит задание последовательности действий по программе, записанной в виде m-файла. Для создания m-файлов может использоваться как встроенный редактор, так и любой текстовый редактор, поддерживающий формат ASCII. Подготовленный и записанный на диск m-файл становится частью системы, и его можно вызывать как из командной строки, так и из другого m-файла. Есть два типа m-файлов: файлы-сценарии и файлы-функции. Важно, что в процессе своего создания они проходят синтаксический контроль с помощью встроенного в систему MATLAB редактора/отладчика m-файлов.
Файл-сценарий, именуемый также Script-файлом, является просто записью серии команд без входных и выходных параметров. Он имеет следующую структуру:
«Основной комментарий %Дополнительный комментарий Тело файла с любыми выражениями. Важны следующие свойства файлов-сценариев:
•они не имеют входных и выходных аргументов;
•работают с данными из рабочей области;
•в процессе выполнения не компилируются;
•представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, что используется в сессии.
Основным комментарием является первая строка текстовых комментариев, а дополнительным — последующие строки. Основной комментарий выводится при выполнении команд lookfor и help имя_каталога. Полный комментарий выводится при выполнении команды help Имя_файла. Рассмотрим следующий файл-сценарий:
%Plot with color red
%Строит график синусоиды линией красного цвета
%с выведенной масштабной сеткой в интервале [xmin.xmax] x=xmin:0.1:xmax;
plot(x,sin(x),'r') grid on
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
43 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Первые три строки здесь — это комментарий, остальные — тело файла. Обратите внимание на возможность задания комментария на русском языке. Знак % в комментариях должен начинаться с первой позиции строки. В противном случае команда help name не будет воспринимать комментарий (иногда это может понадобиться) и возвратит сообщение вида No help comments found in-name.m.
Обратите внимание на то, что такой файл нельзя запустить без предварительной подготовки, сводящейся к заданию значений переменным xmin и хтах, использованным в теле файла. Это следствие первого свойства файлов-сценариев — они работают с данными из рабочей области. Переменные, используемые в файлах-сценариях, являются глобальными, т. е. они действуют одинаково в командах сессии и внутри программного блока, которым является файл-сценарий. Поэтому заданные в сессии значения переменных используются и в теле файла. Имена файлов-сценариев нельзя использовать в качестве параметров функций, поскольку файлы-сценарии не возвращают значений. Можно сказать, что файл-сценарий — это простейшая программа на языке программирования MATLAB
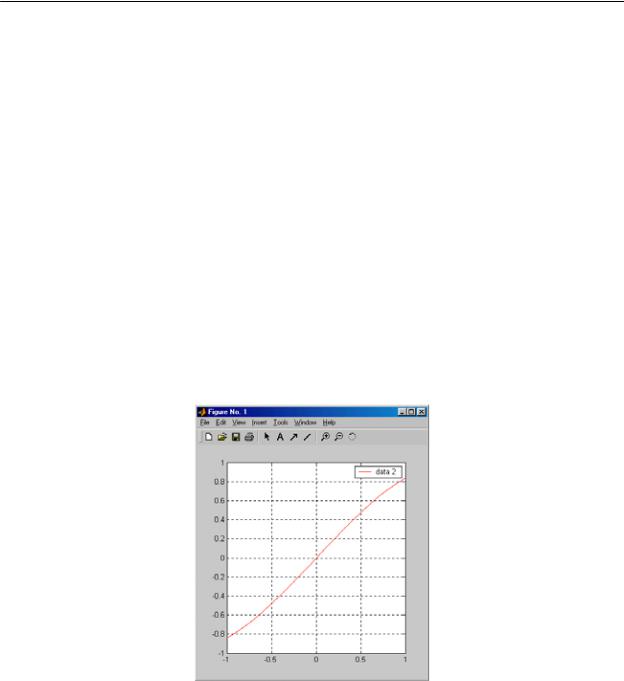
Рисунок 15 - . Пример работы с файлом pcr
Статус переменных в функциях
Переменные, указанные в списке параметров функции, являются локальными и служат для переноса значений, которые подставляются на их место при вызовах функций.
Эта особенность переменных-параметров хорошо видна при разборе примера, показанного на рисунке 15. Здесь (признаемся, что неточно) задана некоторая функция двух переменных fun(x, у).
В этом примере в окне редактора создана функция fun двух переменных х и у, вычисляющая z = х2P +P у2P .P Поскольку переменные х и у указаны как параметры функции fun(x, у), то они являются локальными. В
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
44 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
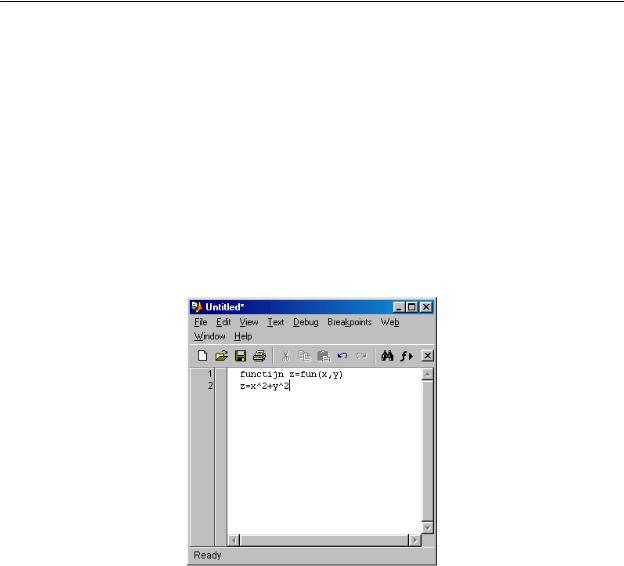
примере вне тела функции им заданы нулевые значения. Очевидно, что при вычислении значения fun(2, 3) в теле функции задается х=2 и у=3. Поэтому результат — z=13. Однако после выхода из тела функции переменные х и у принимают свои исходные значения, равные нулю. Так что эти переменные меняют свои значения на значения параметров функции только локально — в пределах тела функции. А каков статус переменной z в нашем примере? Она, как и любая переменная, определенная в теле функции, также будет локальной. Изначально ее значение не определено. В теле функции переменная принимает значение z=13. А после возврата из функции, как нетрудно увидеть из рисунка 16, переменная z, несмотря на ее применение в теле функции, остается неопределенной. На это указывает сообщение, отображаемое после попытки вывода значения переменной z.
Рисунок 16 - Пример, поясняющий действие локальных и глобальных переменных при задании файла-функции
Возврат из функции производится после обработки всего тела функции, т. е. при достижении конца файла функции. При использовании в теле функции условных операторов, циклов или переключателей иногда возникает необходимость осуществить возврат функции раньше, чем будет достигнут конец файла. Для этого служит команда return. В любом случае, результатом, возвращаемым функцией, являются значения выходных параметров (в нашем случае выходным параметром является переменная z), присвоенные им на момент возврата.
У нашей функции имеется один недостаток — вывод на индикацию значения z=13 из тела функции, хотя после этого z остается равным 0. Чтобы убрать побочный эффект вывода значения z, достаточно установить знак ; после математического выражения, определяющего z. Таким образом, окончательно наша функция должна записываться следующим образом: function z=fun(x,y)
z=x^2+y^2;
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
45 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Этот пример наглядно показывает, что пропуск любого слова или даже простого оператора может привести к не сразу понятным побочным эффектам и даже неверной работе функции
Структура М-файла-функции
М-файл-функция является типичным объектом языка программирования системы MATLAB. Одновременно он является полноценным модулем с точки зрения структурного программирования, поскольку содержит входные и выходные параметры и использует аппарат локальных переменных. Структура такого модуля с одним выходным параметром выглядит следующим образом:
function var=f_name(Cnncoк_napaмeтpов) %Основной комментарий %Дополнительный комментарий Тело файла с любыми выражениями vаr=выражение
М-файл-функция имеет следующие свойства:
•он начинается с объявления function, после которого указывается имя переменной var — выходного параметра, имя самой функции и список ее входных параметров;
•функция возвращает свое значение и может использоваться в виде name (Список_параметров) в математических выражениях;
•все переменные, имеющиеся в теле файла-функции, являются локальными, т. е. действуют только в пределах тела функции;
•файл-функция является самостоятельным программным модулем, который общается с другими модулями через свои входные и выходные параметры;
•правила вывода комментариев те же, что у файлов-сценариев;
•файл-функция служит средством расширения системы MATLAB;
•при обнаружении файла-функции он компилируется и затем исполняется, а созданные машинные коды хранятся в рабочей области
системы MATLAB.
Последняя конструкция vаr=выражение вводится, если требуется, чтобы функция возвращала результат вычислений.
Приведенная форма файла-функции характерна для функции с одним выходным параметром. Если выходных параметров больше, то они указываются в квадратных скобках после слова function. При этом структура модуля имеет следующий вид:
function [varl,var2....]=f_name(Список_параметров) %Основной комментарий %Дополнительный комментарий Тело файла с любыми выражениями
vаr1=выражение vаr2=выражение
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
46 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Такая функция во многом напоминает процедуру. Ее нельзя слепо использовать непосредственно в математических выражениях, поскольку она возвращает не единственный результат, а множество результатов — по числу выходных параметров. Если функция используется как имеющая единственный выходной параметр, но имеет ряд выходных параметров, то для возврата значения будет использоваться первый из них. Это зачастую ведет к ошибкам в математических вычислениях. Поэтому, как отмечалось, данная функция используется как отдельный элемент программ вида:
[varl,va2,... ]=f_nаmе(Список_параметров)
После его применения переменные выхода varl, var2,... становятся определенными и их можно использовать в последующих математических выражениях и иных сегментах программы. Если функция используется в виде nаmе(Список_параметров), то возвращается значение только первого выходного параметра — переменной varl.
Статус переменных и команда global
Итак, из сказанного ясно, что переменные в файлах-сценариях являются глобальными, а в файлах-функциях — локальными. Нередко применение глобальных переменных в программных модулях может приводить к побочным эффектам. Применение локальных переменных устраняет эту возможность и отвечает требованиям структурного программирования.
Однако передача данных из модуля в модуль в этом случае происходит только через входные и выходные параметры, что требует тщательного планирования такой передачи. Так при создании файлов-функций порой желательно применение глобальных переменных. Ответственность за это должен брать на себя программист, создающий программные модули.
Команда global varl var2... позволяет объявить переменные модуляфункции глобальными. Таким образом, внутри функции могут использоваться и такие переменные, если это нужно по условиям решения вашей.
Обработка ошибок
Вывод сообщений об ошибках
Часто в ходе вычислений возникают ошибки. Например, мы уже сталкивались с проблемой вычисления функции sin(x)/x — при х = 0 имеет место ошибка вида «деление на ноль». При появлении ошибки вычисления могут завершиться досрочно с выводом сообщения об ошибке. Следует, однако, отметить, что не все ошибки вызывают остановку вычислений. Некоторые сопровождаются только выдачей предупреждающей надписи.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
47 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Такие ситуации должны учитываться программистом, отмечаться как ошибочные и по возможности устраняться. Для вывода сообщения об ошибке служит команда error('Сообщение об ошибке'), при выполнении которой вычисления прерываются и выдается сообщение об ошибке, заданное в апострофах. Ниже дан пример вычисления функции sd(x)=sin(x)/x, в котором задано сообщение об ошибке на русском языке:
function f=sd(x)
if x==0 error('Ошибка - деление на 0'); end; f=sin(x)/x;
Особенности выполнения m-файлов функций
М-файлы-функции могут использоваться как в командном режиме, так и вызываться из других M-файлов. При этом необходимо указывать все входные и выходные параметры. Исключением является случай, когда выходной параметр единственный — в этом варианте функция возвращает единственный результат и может использоваться в математических выражениях. При использовании глобальных переменных они должны быть объявлены во всех m-файлах, используемых в решении заданной задачи, и во всех входящих в них встроенных подфункциях.
Имена функций должны быть уникальными. Это связано с тем, что при обнаружении каждого нового имени MATLAB проверяет, относится ли это имя к переменной, подфункции в данном m-файле, частной функции в каталогах PRIVATE или функции в одном из каталогов пути доступа. Если последняя встречается, то будет исполнена именно эта функция. В новой версии MATLAB возможно переопределение функции, но это не рекомендуется делать подавляющему большинству пользователей системы.
Если аргумент функции используется только для вычислений и его значения не меняются, то аргумент передается ссылкой, что уменьшает затраты памяти. В других случаях аргумент передается значением. Для каждой функции выделяется своя (рабочая) область памяти, не входящая в область, предоставляемую системе MAT-LAB. Глобальные переменные принадлежат ряду областей памяти. При их изменении меняется содержимое всех этих областей.
Управляющие структуры
Помимо программ с линейной структурой, инструкции которых исполняются строго по порядку, существует множество программ, структура которых нелинейна. При этом ветви программ могут выполняться в зависимости от определенных условий, иногда с конечным числом повторений — циклов, иногда в виде циклов, завершаемых при выполнении заданного условия. Практически любая серьезная программа имеет нелинейную структуру. Для создания таких программ необходимы специальные управляющие структуры. Они имеются в любом языке программирования, и в частности в MATLAB.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
48 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Диалоговый ввод
Приведем простой пример диалоговой программы
% Вычисление длины окружности с диалоговым вводом радиуса r=0;
while r>=0,
r=input('Введите радиус окружностиr=');
if r>=0 disp(' Длина окружности l='); disp(2*pi*r), end end
Эта программа служит для многократного вычисления длины окружности по вводимому пользователем значению радиуса г. Обратите внимание на то, что здесь мы впервые показываем пример организации простейшего диалога.
При выполнении этой команды вначале выводится запрос в виде строки, затем происходит остановка работы программы и ожидается ввод значения радиуса г (в общем случае числа). Ввод, как обычно, подтверждается нажатием клавиши Enter, после чего введенное число присваивается переменной г. Следующая строка
if r>=0 disp(' Длина окружности l = '); disp(2*pi*r), end
с помощью команды disp при r>=0 выводит надпись «Длина окружности 1=» и вычисленное значение длины окружности. Она представляет собой одну из наиболее простых управляющих структур типа if...end. В данном случае она нужна для остановки вычислений, если вводится отрицательное значение г (прием, который любят начинающие программисты).
Приведенные строки включены в управляющую структуру while...end. Это необходимо для циклического повторения вычислений с вводом значений r. Пока r>=0. цикл повторяется. Но стоит задать r<0, вычисление длины окружности перестает выполняться, а цикл завершается.
Если данная программа записана в виде m-файла circ.m, то работа с ней будет выглядеть следующим образом:
» circ
Введите радиус окружности R=1 Длина окружности l=
6.2832
Введите радиус окружности R=2 Длина окружности l=
12.5664
Введите радиус окружности R=-1
»
Итак, на примере даже простой программы мы видим пользу применения управляющих структур типа if...end и whi1e...end, а также функций диалогового ввода input('String') и вывода disp. Обратите внимание на завершение работы программы при вводе любого отрицательного числа для радиуса окружности.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
49 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Функция Input может использоваться и для ввода произвольных строковых выражений. При этом она задается в следующем виде:
input('Комментарий',V)
При выполнении этой функции она останавливает вычисления и ожидает ввода строкового комментария. После ввода возвращается набранная строка.
Условный оператор
Условный оператор if в общем виде записывается следующим образом:
if Условие Инструкции_1 elself Условие Инструкции_2 else
Инструкции_3 end
Эта конструкция допускает несколько частных вариантов. В простейшем, типа! f...end: if Условие Инструкции end
Пока Условие возвращает логическое значение 1 (то есть «истина»), выполняются Инструкции, составляющие тело структуры if...end. При этом оператор end указывает на конец перечня инструкций. Инструкции в списке разделяются оператором , (запятая) или ; (точка с запятой). Если Условие не выполняется (дает логическое значение 0, «ложь»), то Инструкции также не выполняются.
Еще одна конструкция
if Условие Инструкции_1 else
Инструкции_2 end
выполняет Инструкции_1, если выполняется Условие, или Инструкции_2 в противном случае.
Условия записываются в виде:
Выражение_1 Оператор_отношения Выражение_2,
причем в качестве Операторов_отношения используются следующие операторы: ==, <, >, <=, >= или ~=. Все эти операторы представляют собой пары символов без пробелов между ними.
Циклы типа for...end
Циклы типа for...end обычно используются для организации вычислений с заданным числом повторяющихся циклов. Конструкция такого цикла имеет следующий вид:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
50 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
for vаr=Выражение. Инструкция. .... Инструкция end
Выражение чаще всего записывается в виде s:d:e, где s — начальное значение переменной цикла var, d — приращение этой переменной и е — конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s :е (в этом случае d=l). Список выполняемых в цикле инструкций завершается оператором end.
Следующие примеры поясняют применение цикла для получения квадратов значений переменной цикла:
»for i=1:5 i^2, end; ans =
1
ans = 4
ans = 9
ans = 16 ans = 25
»for x=0:.25:1 Х^P 2,P end; ans =
0
ans = 0.0625 ans = 0.2500 ans = 0.5625 ans = 1
Оператор continue передает управление в следующую итерацию цикла, пропуская операторы, которые записаны за ним, причем во вложенном цикле он передает управление на следующую итерацию основного цикла. Оператор break может использоваться для досрочного прерывания выполнения цикла. Как только он встречается в программе, цикл прерывается.
Следует отметить, что формирование матриц с помощью оператора : (двоеточие) обычно занимает намного меньше времени, чем с помощью цикла. Однако применение цикла нередко оказывается более наглядным и понятным. MATLAB допускает использование в качестве переменной цикла массива А размера тхп. При этом цикл выполняется столько раз, сколько столбцов в массиве А, и на каждом шаге переменная var представляет собой вектор, соответствующий текущему столбцу массива А:
»А=[1 2 3:4 5 6]
А = 1 2 3 4 5 6
»for var=A; var, end var =
1
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
51 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
4
var = 2 5
var=
3
6
Циклы типа while...end
Цикл типа while выполняется до тех пор, пока выполняется Условие: while Условие Инструкции end
Досрочное завершение циклов реализуется с помощью операторов break или continue.
Конструкция переключателя
Для осуществления множественного выбора (или ветвления) используется конструкция с переключателем типа switch:
switch switch_Bыражение case саsе_Выражение Список_инструкций
case {саsе_Выражение1, Саsе_выражение2, саsе_ВыражениеЗ....} Список_инструкций
otherwise. Список_инструкций end
Если выражение после заголовка switch имеет значение одного из выражений саsе_Выражение..., то выполняется блок операторов case, в противном случае — список инструкций после оператора otherwise. При выполнении блока case исполняются те списки инструкций, для которых сазе_Выражение совпадает со switch_выражением. Обратите внимание на то, что саsе_Выражение может быть числом, константой, переменной, вектором ячеек или даже строчной переменной. В последнем случае оператор case истинен, если функция strcmp (значение, выражение) возвращает логическое значение «истине».
Поясним применение оператора switch на примере m-файла xz1.m: switch van
case {1,2,3} disp(‘Первый квартал') case {4,5,6} disp('Второй квартал') case {7,8,9} disp('Третий квартал') case {10,11,12} disp(Четвертый квартал') otherwise
disp('Ошибка в задании') end
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
52 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Эта программа в ответ на значения переменной van — номера месяца
— вычисляет, к какому кварталу относится заданный месяц, и выводит соответствующее сообщение:
>>van=1 van =
1
>>xz1
Первый квартал
>>van=7 van =
7
>>xz1
Третий квартал
>>van=11 van =
11
>>xz1
Четвертый квартал
>>van=15 van =
15
>>xz1
Ошибка в задании
Конструкция try...catch...end
В MATLAB 6 введена новая конструкция блока вывода ошибок try...catch...end:
try.
Список инструкций Список инструкций catch. Список инструкций
...
Список инструкций end
Эта конструкция выполняет все списки инструкций. Если в каком-то списке до оператора catch появляется ошибка, то выводится сообщение об ошибке, но системная переменная последней ошибки lasterr не меняется. В сообщениях после catch сообщения об ошибке не выводятся.
Создание паузы в вычислениях
Для остановки программы используется оператор pause. Он используется
вследующих формах:
•pause — останавливает вычисления до нажатия любой клавиши;
•pause(N) — останавливает вычисления на N секунд;
•pause on — включает режим отработки пауз;
•pause off — выключает режим отработки пауз.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
53 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Следующий пример поясняет применение команды pause: for i=1:20;
x=rand(i,40);
y=rand(i,40);
z=sin(x+i*y);
tri = delaunay(x,y); trisurf(tri,x,y,z) pause(1);
end
Команда pause(1) здесь обеспечивает показ 20 рисунков — построений трехмерных поверхностей из треугольных окрашенных областей со случайными параметрами.
2.2 Задание к лабораторной работе.
Реализовать в виде скрипта и функции:
Вариант |
Задание |
1. |
Сортировку массива; |
2. |
Вычисление длины массива; |
3. |
Перестановку начала и конца массива; |
4. |
Вычисление максимального элемента; |
5. |
Вычисление суммы всех элементов массива; |
6. |
Выделение чётных элементов массива; |
7. |
Замену всех элементов меньше заданного, на их квадратный корень; |
8. |
Вычисление среднеквадратичного значения элементов массива; |
9. |
Выделение элементов массива не кратных заданному числу; |
10. |
Перестановку соседних элементов массива; |
11. |
Исключение элементов кратных заданному числу. |
12. |
Вычисление процентов от заданного числа; |
13. |
Генерацию массива чисел в заданных пределах, с заданным шагом; |
14. |
Замену в массиве заданных чисел на отрицательные. |
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
54 |
|
|
|
|
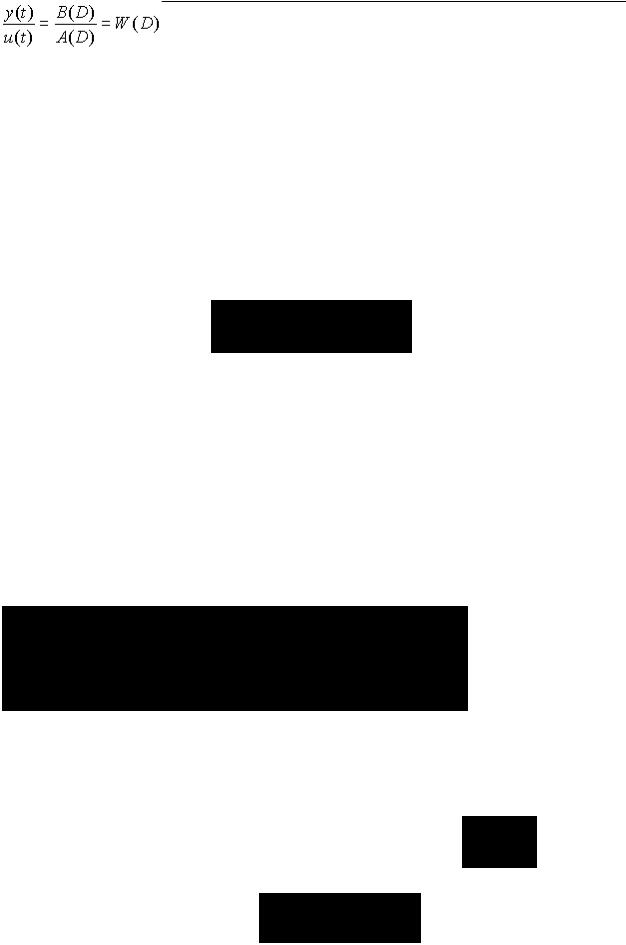
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №3 Динамические характеристики систем автоматического управления
Цель работы: Ознакомление с динамическими характеристиками систем автоматического управления (САУ) и получение навыков исследования линейных динамических моделей.
3.2Постановка задачи
Вкачестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов:
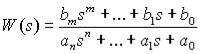 .
.
Необходимо:
1. Определить полюса и нули передаточной функции: 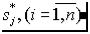 ,
, 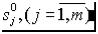 .
.
2.Записать дифференциальное уравнение, определяющее функционирование САУ.
3.Построить графики переходной и импульсно-переходной функции: h(t), w(t).
3.3Краткие теоретические сведения
Рассмотрим систему автоматического управления (САУ), описываемую
линейным (линеаризованным) дифференциальным уравнением вида:
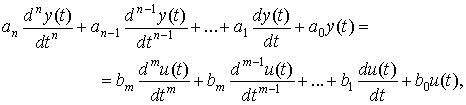 (1.1)
(1.1)
где u(t) – входной процесс, y(t) – выходной процесс, aiB ,B bjB ,B ( ) – постоянные коэффициенты, n, m (n ³ m) – постоянные числа. В операторной форме выражение (1.1) может быть записано –
) – постоянные коэффициенты, n, m (n ³ m) – постоянные числа. В операторной форме выражение (1.1) может быть записано –
 .
.
Здесь D – оператор дифференцирования  . Отсюда преобразование “вход-выход” системы –
. Отсюда преобразование “вход-выход” системы –
, |
(1.2) |
где W(D) называется операторной передаточной функции.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
55 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Один из способов моделирования систем заключается в представлении преобразования “вход-выход” в виде комплексной передаточной функции:
, |
(1.3) |
которая получается путем применения преобразования Лапласа к (1.2) при начальных нулевых условиях. Здесь s-комплексная переменная. Связь между операторной (1.2) и комплексной (1.3) передаточными функциями можно записать в виде
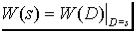 .
.
Комплексные числа, являющиеся корнями многочлена В(s), называются нулями передаточной функции, а корни многочлена A(s) – полюсами.
Явный вид связи входа и выхода определяется выражением:
, |
(1.4) |
где w(t) – оригинал (т.е. полученный с помощью обратного преобразования Лапласа) комплексной передаточной функции W(s).
Динамические свойства систем характеризуют реакции на входные воздействия специального вида. В частности анализ выхода системы на единичный скачок и d -функцию (дельта-функцию).
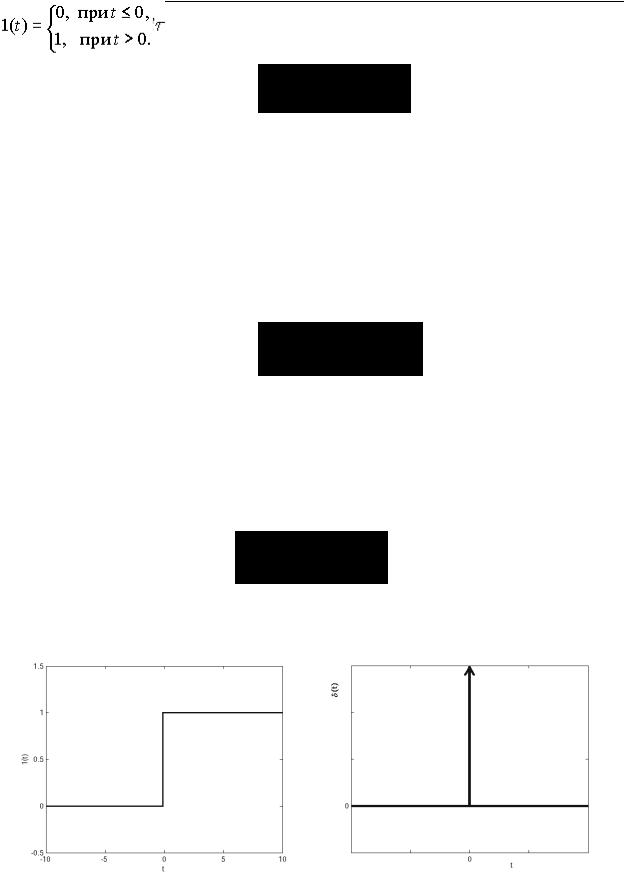
Пусть u(t) = 1(t), то есть на вход системы подается функция Хевисайда (единичный скачок), определяемая
График функции Хевисайда приведен на рисунке 2а. Реакция САУ на единичный скачек называется переходной функцией системы и обозначается h(t).
а) |
б) |
Рисунок 2 - |
а) Функция Хевисайда. б) Функция Дирака. |
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
56 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Если u(t) = d (t), то есть на вход системы поступает функция Дирака (d - функция, импульсная функция, рисунок 1.1б) определяемая
то реакция САУ называется импульсной переходной функцией системы и обозначается w(t). Таким образом оригинал комплексной передаточной функции можно измерить как реакцию систему на импульс.
Импульсная и переходная функции системы связаны соотношением (из
(1.4)):
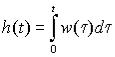 .
.
3.4Последовательность выполнения работы
Для выполнения лабораторной работы используется пакет прикладных
программ (ППП) Control System Toolbox. ППП предназначен для работы с
LTI-моделями (Linear Time Invariant Models) систем управления. (Сведения по работе с LTI-моделями приведены в приложении 4)
В Control System Toolbox имеется тип данных, определяющих динамическую систему в виде комплексной передаточной функции. Синтаксис команды, создающий LTI-систему c одним входом и одним выходом в виде передаточной функции:
TF([bmB ,B …, b1B ,B b0B B], [aBn,B …, a1B B, a0B B])
bmB ,B …, b1B B – значения коэффициентов полинома В в (1.3), anB ,B …, a1B B – значения коэффициентов полинома A в (1.3).
Для выполнения работы могут применяться команды, приведенные в таблице 2.
 Синтаксис
Синтаксис
 pole(<LTI-объект>)
pole(<LTI-объект>)
 zero(<LTI-объект>)
zero(<LTI-объект>)
 step(<LTI-объект>)
step(<LTI-объект>)
 impulse(<LTI-объект>)
impulse(<LTI-объект>)
 bode(<LTI-объект>)
bode(<LTI-объект>)  nyquist(<LTI-объект>)
nyquist(<LTI-объект>)
Таблица 2. - Некоторые команды
Control System Toolbox
 Описание
Описание
 Вычисление полюсов передаточной функции
Вычисление полюсов передаточной функции
 Вычисление нулей передаточной функции
Вычисление нулей передаточной функции
 Построение графика переходного процесса
Построение графика переходного процесса
Построение графика импульсной переходной функции
Построение логарифмических частотных характеристик (диаграммы Боде)
 Построение частотного годографа Найквиста
Построение частотного годографа Найквиста
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
57 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Для определения корней полиномов степени k, может, также, применятся команда MATLAB roots(P), которая, в качестве аргумента P, получает матрицу коэффициентов полинома [pkB ,B …, p0B B].
Другим вариантом получения графиков динамических характеристик САУ является использование графического интерфейса ППП CST – LTI viewer, вызов которого осуществляется командой ltiview которой, в качестве параметра, можно указать имя переменной, содержащей LTI-объект.
Таким образом, выполнение лабораторной работы состоит из следующих шагов:
1.Изучить теоретические сведения.
2.Запустить систему MATLAB.
3.Создать tf-объект, в соответствии с заданным вариантом.
4.Составить дифференциальное уравнение, определяющее функционирование САУ.
5.Определить полюса передаточной функции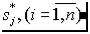 с использованием команды roots или pole.
с использованием команды roots или pole.
6.Определить нули передаточной функции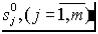 с использованием команды roots или zero.
с использованием команды roots или zero.
Используя LTI-viewer, или соответствующие команды (таблица 1) получить динамические характеристики – переходную функцию h(t), импульсно-переходную функцию w(t).
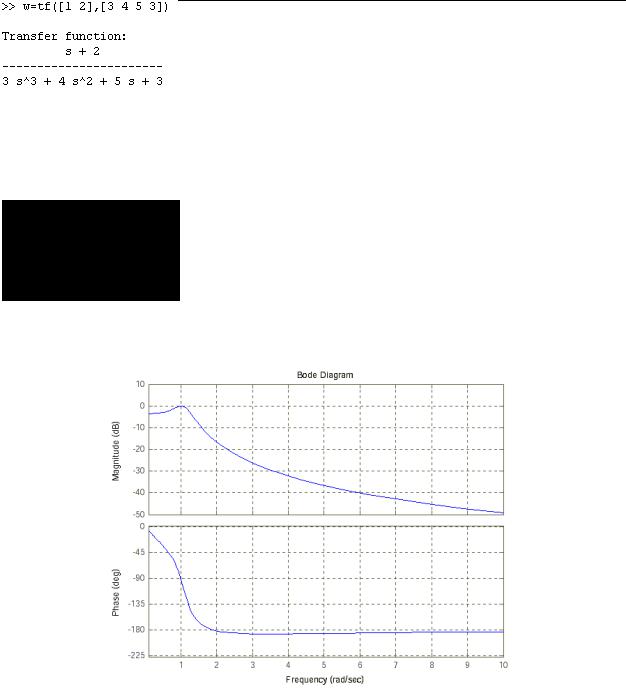
3.5Пример
Задана передаточная функция САУ
 .
.
Найдем ее динамические и частотные характеристики. Будем работать в командном режиме среды MATLAB.
1.Создадим LTI-объект с именем w, для этого выполним:
2.Найдем полюса и нули передаточной функции с использованием команд pole, zero.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
58 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
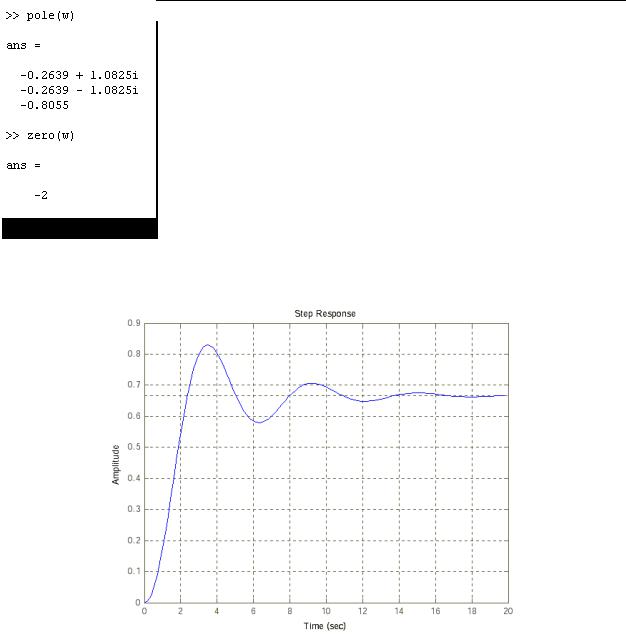
3. Построим переходную функцию командой step(w). Результат ее выполнения приведен на рисунок 3.
Рисунок 3 - Переходная функция h(t).
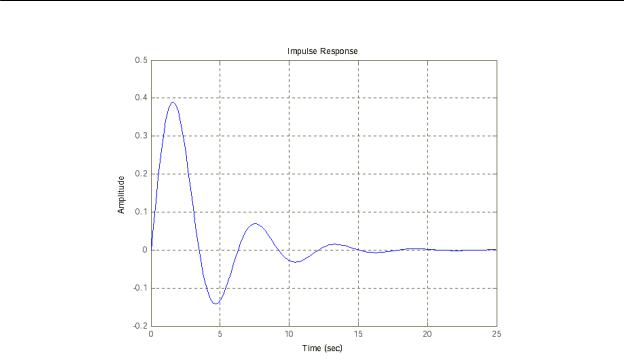
4. Построим импульсную переходную функцию командой impulse(w). Результат показан на рисунке 4.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
59 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рисунок 4 - Импульсная переходная функция.
3.6Контрольные вопросы
1.Представьте систему в виде последовательного соединения типовых звеньев.
2.Дайте определение и поясните физический смысл переходной функции.
3.Представьте исходную систему в пространстве состояний.
4.Найдите передаточную функцию замкнутой системы.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
60 |
|
|
|
|
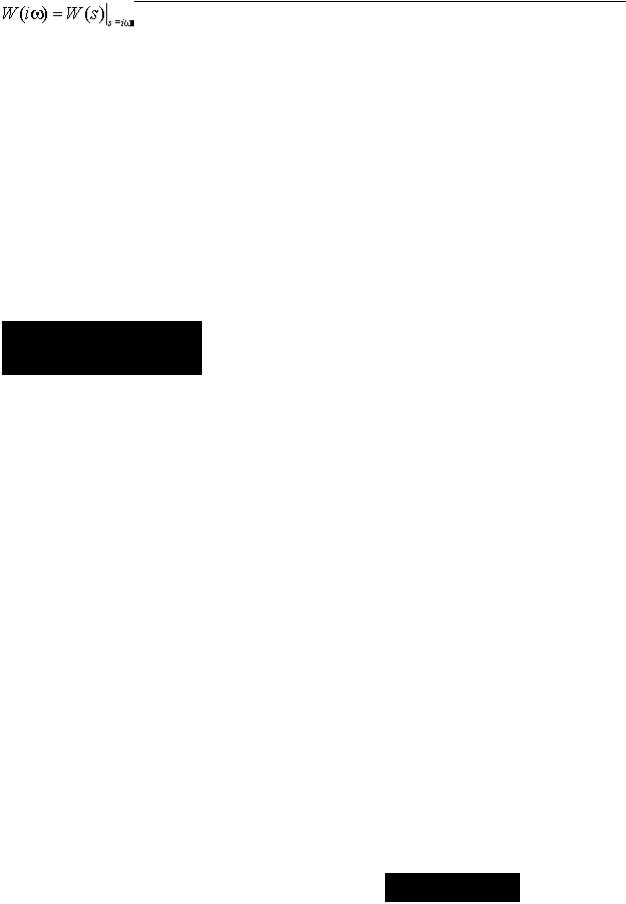
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №4 Частотные характеристики систем автоматического управления
Цель работы: Ознакомление с частотными характеристиками систем автоматического управления (САУ) и получение навыков исследования линейных динамических моделей.
4.1Постановка задачи
Вкачестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов
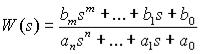 .
.
Необходимо:
1.Построить логарифмические частотные характеристики
L (w ).
2.Построить частотный годограф Найквиста
W(iw ), w = [0, ¥ ].
3.Представить исходную систему в виде последовательного соединения типовых звеньев. Построить характеристики этих типовых звеньев.
4.2Краткие теоретические сведения
Благодаря широкому применению при исследовании устойчивости
динамических систем и проектировании регуляторов получили распространение частотные характеристики.
Пусть на вход системы с передаточной функцией W(s) подается
гармонический сигнал |
|
u(t) = auB B cos(w t), t >0. |
(1.5) |
В этих условиях справедлива следующая теорема: |
|
Если звено является устойчивым, то установившаяся реакция y(t) на гармоническое воздействие является функцией той же частоты с амплитудой
ayB B = auB B |W(iw )|,
и относительным сдвигом по фазе y = arg W(iw ).
Таким образом, выход определяется гармонической функцией y(t) = auB B |W(iw )| cos(w t + arg W(iw )),
2 |
|
= –1), |
– частотная |
где i – комплексная единица (iP |
P |
характеристика.
Частотной характеристикой W(iw ) стационарной динамической системы называется преобразование Фурье переходной функции:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
61 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
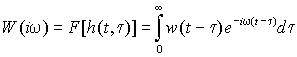 ,
,
где w(t – t ) – импульсная переходная функция.
Связь между комплексной передаточной функцией и частотной характеристикой, исходя из свойств преобразований Фурье можно представить в виде соотношения:
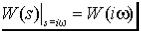 .
.
При фиксированном значении w частотная характеристика является комплексным числом, и, следовательно, может быть представлена в виде
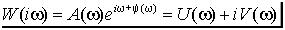 .
.
Здесь 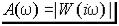 – амплитудно-частотная характеристика (АЧХ);
– амплитудно-частотная характеристика (АЧХ);
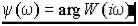 – фазово-частотная характеристика (ФЧХ);
– фазово-частотная характеристика (ФЧХ);
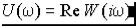 – вещественная частотная характеристика (ВЧХ);
– вещественная частотная характеристика (ВЧХ);
 – мнимая частотная характеристика (МЧХ). Геометрическое место точек W(iw ) на комплексной плоскости при
– мнимая частотная характеристика (МЧХ). Геометрическое место точек W(iw ) на комплексной плоскости при
изменении w от w 0B B до от w 1B B (обычно w 0B =B 0, w 1B B = ¥ ), называется амплитудно-фазовой характеристикой (АФХ) или частотным годографом Найквиста.
Имеет широкое практическое значение диаграмма Боде (логарифмическая амплитудная характеристика, ЛАХ), которая определяется как L = 20 lg A(w ), измеряется в децибелах и строится как функция от lg w .
4.3 Последовательность выполнения работы
Для выполнения лабораторной работы используется пакет прикладных программ (ППП) Control System Toolbox. ППП предназначен для работы с
LTI-моделями (Linear Time Invariant Models) систем управления.
Таким образом, выполнение лабораторной работы состоит из следующих шагов:
1.Изучить теоретические сведения.
2.Запустить систему MATLAB.
3.Создать tf-объект, в соответствии с заданным вариантом.
4.Составить дифференциальное уравнение, определяющее функционирование САУ.
5.Используя LTI-viewer, или соответствующие команды (табл.1) частотные характеристики – диаграмму Боде, частотный годограф Найквиста.
6.Получить представление исходной функции в виде произведения типовых звеньев.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
62 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
4.4 Пример
Задана передаточная функция САУ
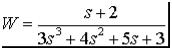 .
.
Найдем ее частотные характеристики. Будем работать в командном режиме среды MATLAB.
1.Создадим LTI-объект с именем w, для этого выполним:
2.Диаграмму Боде получим, используя команду bode(w) – рисунок 5.
Рисунок 5 - Логарифмические частотные характеристики.
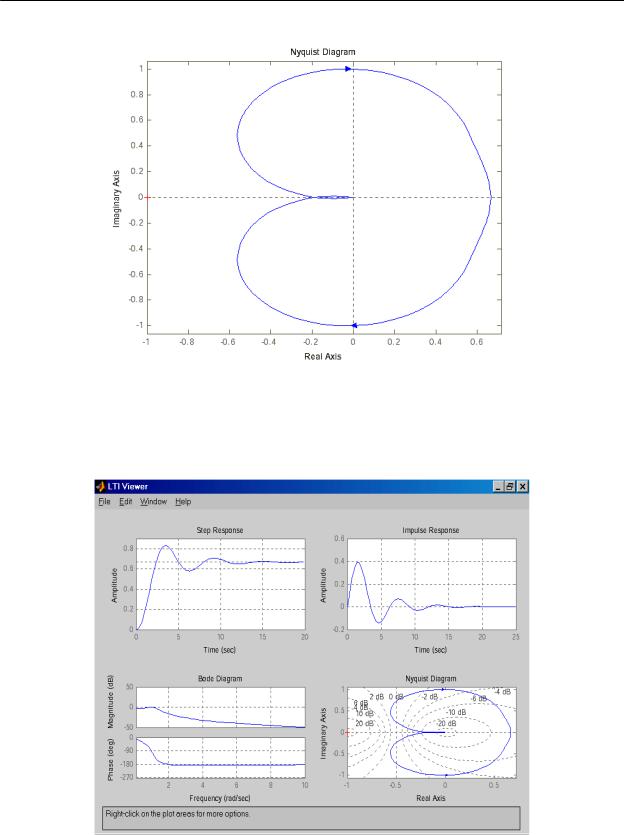
3. Определим частотный годограф Найквиста, выполнив команду nyquist(w)
– рисунок 6.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
63 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рисунок 6 - Частотный годограф.
Аналогичные результаты (рисунок 7) можно получить, используя команду ltiview(w), с соответствующими настройками в меню “Plot Configuration”.
Рисунок 7 - LTI-viewer.
Каждая из построенных характеристик полностью и однозначно определяет рассматриваемую систему управления.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
64 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №5 Анализ и синтез САУ методом коневого годографа
с использованием Control System Toolbox
Цель работы: научиться строить корневой годограф и вычислять граничные коэффициенты устойчивости системы.
5.1Краткие теоретические сведения
Вряде случаев, имеющих практическое значение, модель линейной системы автоматического управления (САУ) задается в виде структурной схемы, состоящей из типовых звеньев, математическое описание которых задано в операторной форме. Связь между входом и выходом системы задается в виде передаточной функции W(s). B общем виде передаточную функцию W(s) можно представить в виде:
W(s)=B(s)/A(s), |
(1) |
где s - комплексная переменная, B(s) - полином степени m; A(s) - полином степени n.
Для физически реализуемых САУ m≤n. Коэффициенты указанных полиномов действительные числа.
Применение метода корневого годографа (КГ) обусловлено фундаментальной зависимостью поведения линейной САУ от полюсов и нулей ее передаточной функции. Под полюсами подразумеваются корни полинома - знаменателя A(s), а под нулями - корни полинома числителя B(s). Полином A(s) называется также характеристическим многочленом передаточной функции W(s).
Положение полюсов W(s) на комплексной плоскости определяет устойчивость САУ, а в совокупности с нулями вид импульсной переходной функции w(t) и переходной функции h(t).
Метод корневого годографа позволяет находить полюса и нули передаточной функции замкнутой системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы k.
Передаточную функцию разомкнутой системы Wp(s) представим в
виде:
(2)
,
где s0P jPB B - нули передаточной функции WpB (B s), ( j =1, n ); s*P jPB B - полюса передаточной функции Wp(s), ( j =1, n ), n и m - порядки знаменателя и числителя; K - коэффициент усиления разомкнутой системы; C - коэффициент представления.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
65 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Передаточная функция разомкнутой системы, как правило, задается в виде отношения произведений передаточных функций стандартных (типовых) звеньев, при описании которых используются выражения трех видов:
T s, |
(3) |
T s + 1, |
(4) |
T 2s 2 + 2T ζ s + 1. |
(5) |
Здесь Т - постоянная времени [с]. |
|
Если выражения (3)-(5) стоят в знаменателе передаточных функций звеньев (в числителе 1), то звенья называются соответственно интегрирующим, апериодическим, колебательным. Для колебательного звена ζ - безразмерный коэффициент затухания (0<ζ<1). Если выражения (3)-(5) стоят в числителе передаточных функций звеньев (1), то звенья называются соответственно дифференцирующим, форсирующим первого порядка, форсирующим второго порядка.
Для перехода от стандартной формы записи к формуле (2) необходимо вычислить полюса и нули соответствующих типовых звеньев.
Для передаточных функций, использующих выражение (3):
|
*(0) |
=0, |
(6) |
|
sP |
||
|
|
P |
|
использующих выражение (4): |
|
|
|
*(0) |
- 1/T, |
(7) |
|
sP |
= |
||
P
использующих выражение (5):
(8)
,
или
(9)
,
где j=arcsin ζ.
Коэффициент представления C вычисляется с помощью выражения:
(10)
,
Для звеньев, использующих выражение (5), соответствующая постоянная времени входит в выражение (10) в квадрате.
При замыкании системы с передаточной функцией Wp(s) единичной обратной связью передаточная функция замкнутой системы Wз(s) принимает вид:
(11)
,
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
66 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
где знак "+" соответствует отрицательной обратной связи; знак "-" соответствует положительной обратной связи.
Структурная схема системы с обратной связью приведена на рисунок 8.
Рисунок 8 - Структурная схема САУ.
Из (11) следует, что нули передаточной функции замкнутой системы равны нулям передаточной функции разомкнутой системы.
Для определения полюсов замкнутой системы необходимо решить уравнение:
Wp(s)= -1. |
(12) |
Так как Wp(s) является функцией комплексного переменного s, то уравнение (12) распадается на два уравнения: уравнение модулей и
|W(s)|=1
уравнение аргументов
arg W(s) = ± (2υ +1)π, υ =0, 1, 2, …
для отрицательной обратной связи и
arg W(s) = ± 2π, υ =0, 1, 2, …,
для положительной обратной связи.
Уравнения (14) имеют наглядный геометрический смысл. Если точка s является полюсом замкнутой системы, то проведя в точку s вектора из всех нулей Wp(s) (обозначим аргументы этих векторов θ0P jPB )B и вектора из всех полюсов Wp(s) (обозначим аргументы этих векторов θP*iPB ),B уравнение (14а) можно записать в следующем виде:
m |
n |
|
∑θ0j − |
∑θ*i = ±(2υ+1)π, υ = 0,1,2,..., |
(15а) |
j=1 |
i=1 |
|
а уравнение (14б) в виде: |
|
|
m |
n |
|
∑θ0j |
−∑θ*i = ±2υπ, υ = 0,1,2,..., |
(15б) |
j=1 |
i=1 |
|
Углы θ отсчитываются от положительного направления действительной оси. Знак угла "+" соответствует повороту против часовой стрелки, знак угла "-" соответствует повороту по часовой стрелке.
Геометрическое место точек на комплексной плоскости "s", удовлетворяющее выражениям (15а) и (15б) называется корневым годографом.
Как следует из (15), конфигурация корневого годографа не зависит от коэффициента усиления K, но каждому конкретному значению K однозначно соответствуют точки на корневом годографе.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
67 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Для определения этого соответствия достаточно воспользоваться уравнением (13) в следующей интерпретации:
|
m |
|
|
|
∏l0j |
|
|
K C |
j=1 |
=1, |
(16) |
n |
|||
|
∏l*i |
|
|
|
i=1 |
|
|
где l0j - модуль (длина) вектора, проведенного из j-нуля в точку s КГ; |
l*i - |
||
модуль вектора, проведенного из i полюса в ту же точку s.
Для систем небольшого порядка m, n <5…7 построение КГ можно осуществлять “вручную” (с помощью транспортира и линейки).
Приведем свойства корневых годографов (случай отрицательной обратной связи):
1.Ветви корневого годографа непрерывны и расположены на комплексной плоскости симметрично относительно действительной оси.
2.Число ветвей КГ равно порядку системы n. Ветви начинаются в n полюсах разомкнутой системы при K=0. При возрастании K от 0 до бесконечности полюса замкнутой системы двигаются по ветвям КГ.
3.Отрезки действительной оси, по которым перемещаются действительные полюса замкнутой системы являются действительными ветвями корневого годографа. Эти ветви находятся в тех частях действительной оси, справа от которых расположено нечетное общее число действительных полюсов и нулей разомкнутой системы.
4.m ветвей КГ при возрастании K от 0 до бесконечности заканчиваются
вm нулях Wp(s), a (n-m) ветвей при K, стремящемся к бесконечности, удаляются от полюсов вдоль асимптот.
5.Асимптоты в виде звезды из (n-m) полупрямых выходят из точки с координатой
|
|
|
m |
n |
|
|
|
∑θ0j −∑θ*i |
|
σ |
|
= |
j=1 |
i=1 |
|
a |
|
n |
−m |
|
|
|
||
на действительной оси под углами:
θa = 2nυ−+m1π, υ = 0,n −m −1
кдействительной оси.
6.Угол выхода θ*P iPB B ветви КГ из полюса s*P iPB B определяется из уравнения (15а), примененного к данному полюсу. Аналогично определяется угол входа ветви КГ в нуль s0P jPB .B
7.При расположении ветвей корневого годографа в левой полуплоскости s САУ устойчива. При пересечении ветвей КГ мнимой оси слева направо САУ становится неустойчивой. Пусть при K=KкрB B пересечение
КГ с мнимой осью произойдет в некоторой точке iωкрB B. Назовем это значение коэффициента усиления критическим KкрB ,B а величину ωкрB B критической угловой частотой, на которой система становится неустойчивой.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
68 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Метод КГ позволяет выбрать коэффициент усиления САУ, подобрать расположение полюсов и нулей передаточной функции корректирующих звеньев, определить параметры доминирующих полюсов САУ (ближайших к началу координат плоскости s).
В качестве примеров, приведем КГ для двух систем автоматического управления.
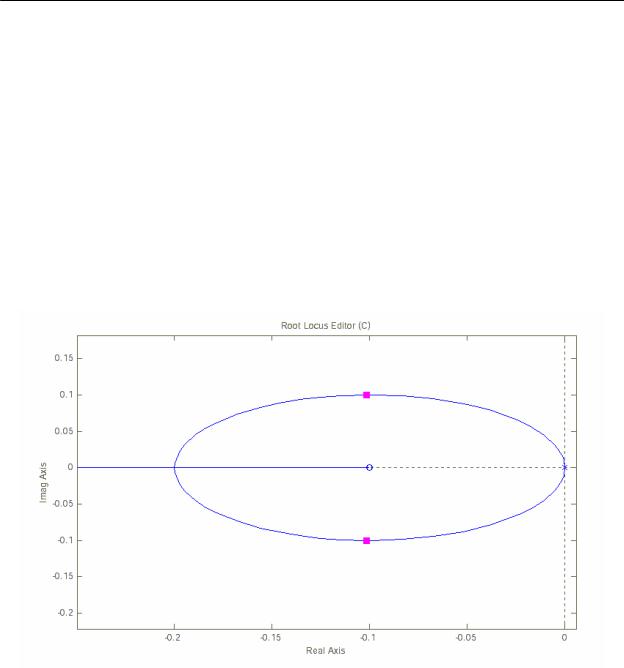
На рис.2,а приведен корневой годограф САУ, передаточная функция разомкнутой системы, которой равна:
Wp1B =K(s+0B .1)/s-P 2.P
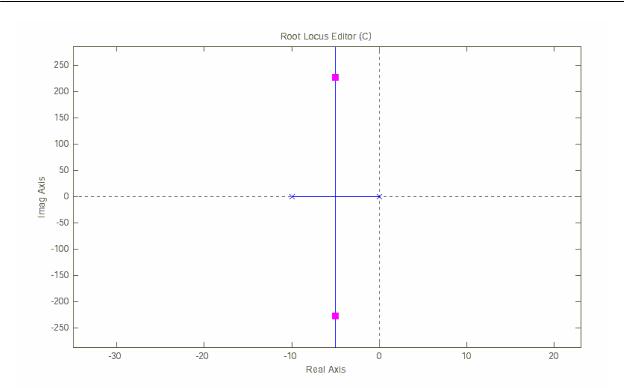
На рисунок 9,б представлен КГ САУ с передаточной функцией разомкнутой системы вида:
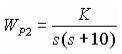 .
.
а)
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
69 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
б)
Рисунок 9 - Примеры корневых годографов.
Построение корневых годографов
Постановка задачи Дана модель разомкнутой системы, записанная в виде отношения
произведений типовых звеньев. Необходимо:
1.Построить корневой годограф.
2.Получить коэффициент усиления KкрB ,B при котором система находится на границе устойчивости.
3.Вычислить частоту ωкрB B, при которой в системе возникают
незатухающие колебания.
Для решения задачи используется GUI-интерфейс “SISO-Design Tool” из пакета прикладных программ Control System Toolbox системы инженерных расчетов MatLab.
Графический интерфейс предназначен для анализа и синтеза одномерных линейных (линеаризованных) систем автоматического управления (SISO - Single Input/Single Output).
В Control System Toolbox имеется тип данных, определяющих динамическую систему в виде набора полюсов, нулей и коэффициента усиления передаточной функции. Синтаксис команды, создающий LTI
(Linear Time Invariant)-систему в виде объекта ZPK (zero-pole-gain) с
одним входом и одним выходом
ZPK([s10 ,...,s0m ], [s1* ,...,s*m ], K),
где s10 ,...,s0m - значения нулей системы, s1* ,...,s*m - значения полюсов системы, K - коэффициент усиления.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
70 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Более естественным является вариант, при котором с помощью функции ZPK создается символьная переменная 's', которая затем используется для определения передаточной функции в виде отношения (2). Например, после выполнения команд:
s=zpk('s'); W1=(s+0.1)/(s^2)
произойдет создание переменной W1 типа ZPK, определяющей передаточную функцию вида:
W1B =K(s+0B .1)/s-P 2.P
Запуск графического интерфейса SISO-Design Tool осуществляется командой sisotool или выбором соответствующего пункта в окне "Launch Pad".
Необходимо выбрать в меню View пункт Root Locus (корневой годограф), для отображения редактора Root Locus Editor. В правом верхнем углу SISO-Design Tool можно менять тип обратной связи (кнопка '+/-') и структурную схему САУ. Предполагается наличие отрицательной обратной связи, и структурной схемы, показанной на рис.1.
Для загрузки данных из рабочего пространства MatLab необходимо использовать меню "File/Import", в результате чего появляется диалог Import System Data. Необходимо, чтобы в результате импортирования данных получилась рассматриваемая схема САУ (см. рис.1). Изменение динамических и частотных характеристик замкнутой системы при изменении К можно проследить используя меню "Tools/Loop Responses".
Задание к лабораторной работе.
Пусть необходимо исследовать САУ с передаточной функцией разомкнутой системы:
W(s) = |
(a s +1) |
, |
s(bs +1)(cs2 +2a ds +1) |
для которой коэффициенты a,b,c,d определяются индивидуальным вариантом.
Рассмотрим пример исследования САУ на следующем наборе коэффициентов:
a=0.2; b=0.1; c=0.04; d=0.3.
1. Создадим ZPK-объект, найдем полюса и нули разомкнутой системы:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
71 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
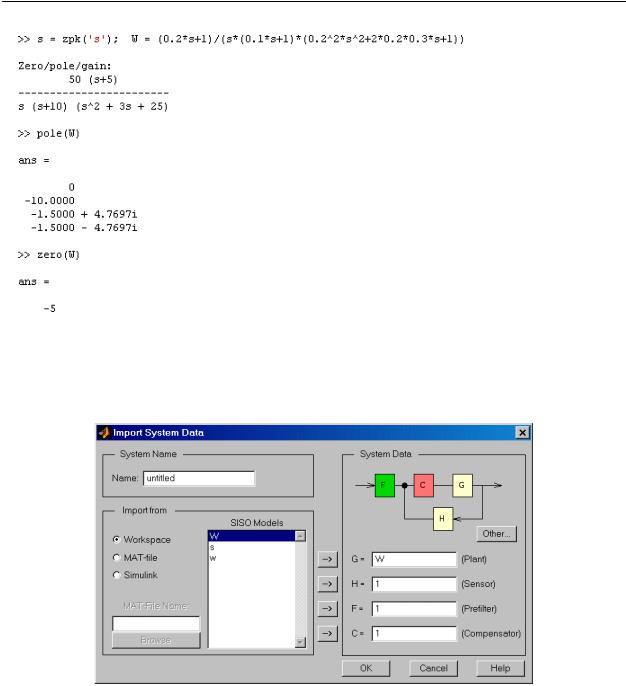
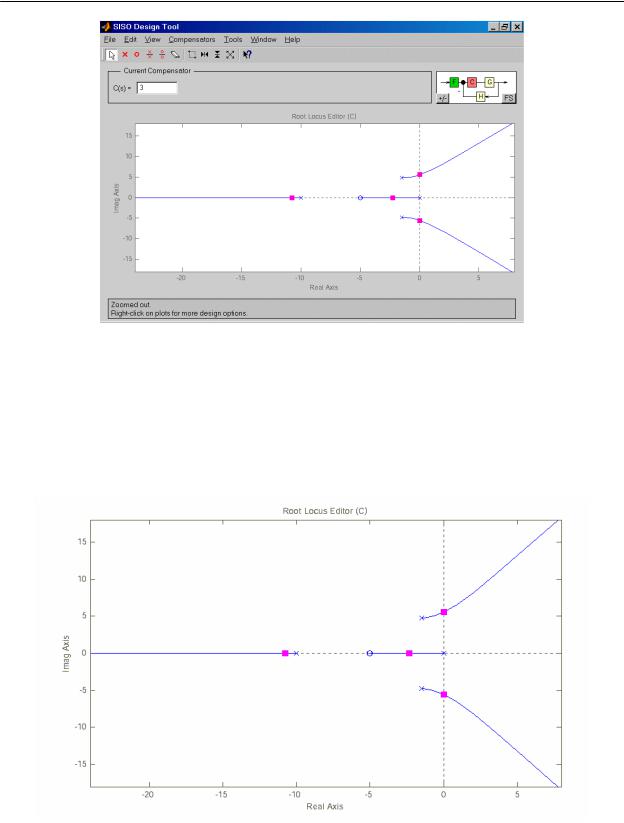
2. Запустим SISO-Design Tool, настроим параметры и импортируем ZPK-объект из рабочего пространства MatLab (рисунок 10). В окне Root Locus Editor интерфейса SISO-Design Tool построится корневой годограф (рисунок 11).
Рисунок 10 - Диалог импортирования данных в SISO-Design Tool.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
72 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рисунок 11 - SISO-Design Tool.
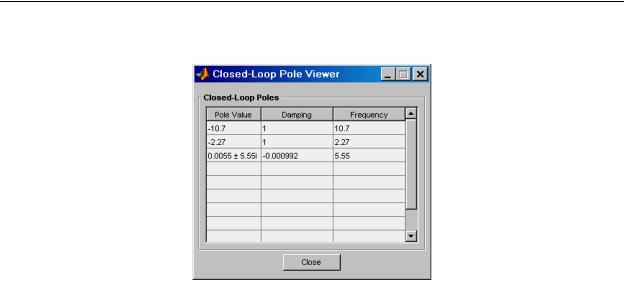
3. Двигая красным курсором по корневому годографу до пересечения ветвей с мнимой осью, определить значение KкрB B (рисунок 5). В данном случае KкрB >>3B . Значение ωBкрB соответствует мнимой координате пересечения КГ мнимой оси. Просмотреть это значение можно в нижней части интерфейса или выбрав меню "View/Closed-Loop Poles" (рисунок 6).
Рисунок 12 - Корневой годограф с нанесенным значением Kкр.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
73 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рисунок 13 - Closed-Loop Poles Viewer.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
74 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №6 Описание динамических систем в пространстве состояний
с использованием Control System Toolbox
Цель работы: научиться строить результирующие системы и исследовать наблюдаемость и управляемость систем.
Постановка задачи
Даны математические модели трех систем и структурная схема, представляющая собой соединение этих систем. Необходимо:
•получить модель результирующей системы в пространстве состояний,
•исследовать наблюдаемость и управляемость трех подсистем в отдельности, и общей системы.
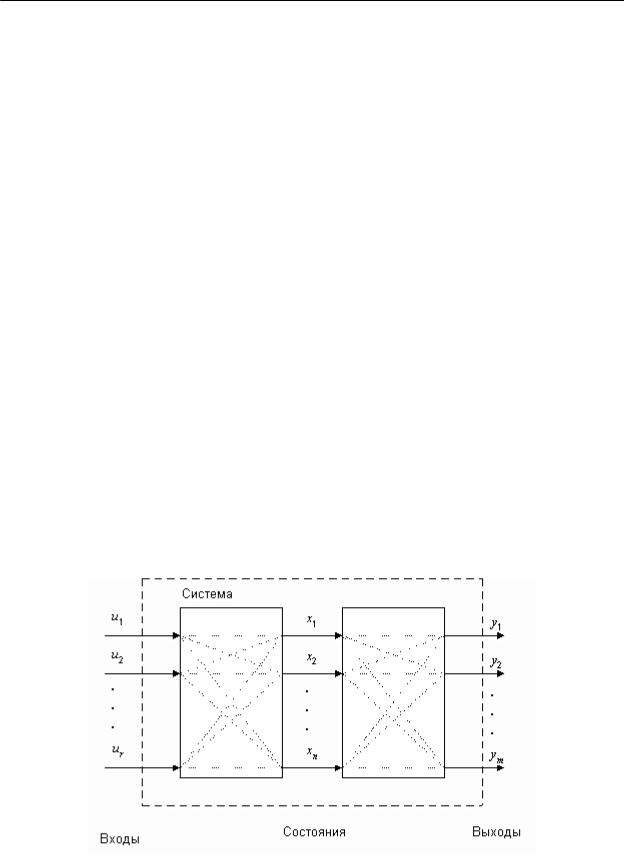
Многомерные системы, в отличие от одномерных имеют несколько входов и несколько выходов.
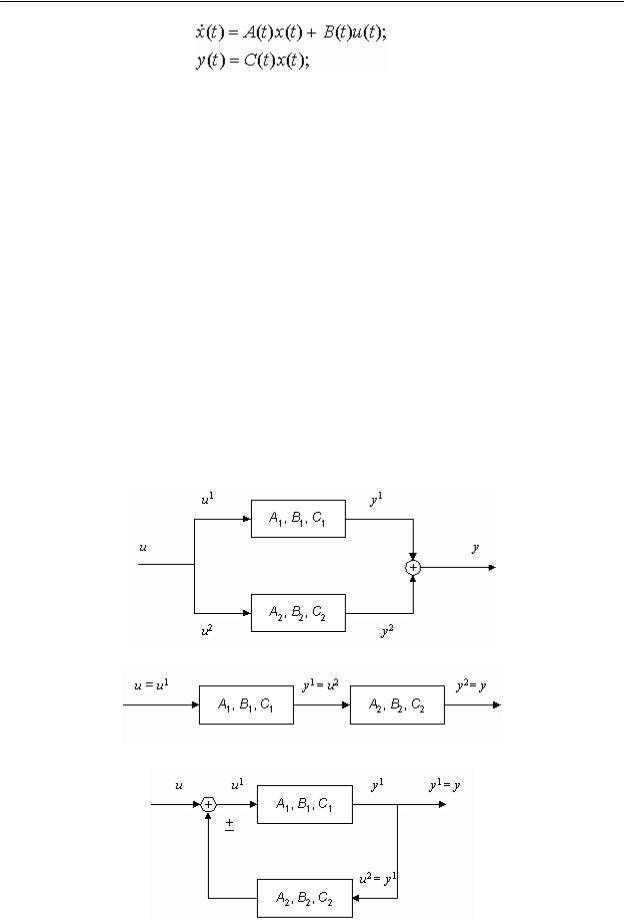
Для описания таких систем используются три набора параметров (три вектора), см. рис.1:
1.вектор входных воздействий (управлений);
2.вектор переменных состояний;
3.вектор выходных параметров,
идва преобразования:
1.преобразование “входы-состояния”;
2.преобразование “состояния-выходы”.
Рис.1. Многомерные системы.
Широкое распространение, обусловленное разработанным математическим аппаратом, получили линейные модели многомерных систем в пространстве состояний, которые имеют вид:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
75 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
(1)
,
первое соотношение называется уравнением состояния, второе - уравнением выхода. Здесь x=(x1B B, x2B ,B …, xnB B)TP P | RnP P - вектор переменных состояний; u=(u1B ,B u2B ,B …, urB )B TP P | U | RnP P - вектор управлений; y=(y1B ,B y2B ,B …, yBm)B TP P | RnP P - вектор измеряемых параметров; t - время; A(t), B(t), C(t) - матрицы размерности (n x n), (n x r), (m x n) соответственно. Предполагается, что известны начальные состояния x(t0B )=B x0B ,B где t0B B - начальный момент времени.
Если матрицы A(t), B(t), C(t) не зависят от времени t, то система называется стационарной. В пакете предполагается, что системы стационарны.
Рассмотрим задачи соединения двух подсистем в систему. При соединении возможны три варианта (см. рис.2): параллельное (а), последовательное (б) и в обратной связи (в). Предполагается, что обе системы описываются в пространстве состояний соотношениями:
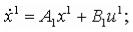 y1P P = C x1P ;P
y1P P = C x1P ;P
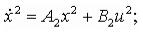 y2P P = C x2P P,
y2P P = C x2P P,
где x1P ,P u1P ,P y1P -P векторы состояний, управлений, выходов первой системы; x2P ,P u2P ,P y2P -P второй системы соответственно. Необходимо по известным матрицам A1B ,B B1B ,B C1B ,B A2B ,B B2B ,B C2B получитьB матрицы A, B, C (см. рис.2г).
a)
б)
в)
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
76 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
г)
Рис.2. Соединение двух систем.
1. Параллельное соединение
Запишем уравнения системы, с учетом особенностей соединения, указанных на рис.2а.
отсюда получаем:
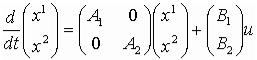 ;
; 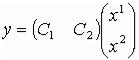 .
.
Окончательно матрицы соединения имеют вид -
.
2. Последовательное соединение:
y=C2B xB 2P ;P
в матричном виде:
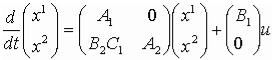 ;
;
окончательно имеем, что:
.
3. Обратная связь:
y = C1B xB 1P ;P
в матричном виде:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
77 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
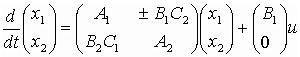 ;
; 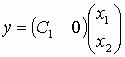 .
.
Следовательно,
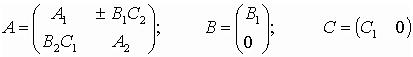 .
.
Для линейных систем справедливо следующие правило, называемое принципом суперпозиции: эффект, вызываемый суммой нескольких воздействий, равен сумме нескольких воздействий, равен сумме эффектов от нескольких воздействий в отдельности. Закон изменения вектора состояний линейной системы представляется в виде суммы свободного и вынужденного колебания: x(t)=xcB (B t)+xвB (B t).
Свободное движение xcB (B t) происходит при отсутствии внешнего воздействия в ненулевых начальных условиях. Оно определяется решением однородной системы уравнений, соответствующей исходному уравнению
состояний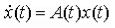 с начальными условиями x(t0B )=B x0B .B
с начальными условиями x(t0B )=B x0B .B
Вынужденное движение xвB B(t) - это реакция системы на внешнее воздействие u(t) при нулевых начальных условиях. Оно определяется решением неоднородного уравнения при нулевых начальных условиях.
Для многомерных нестационарных систем, описываемых соотношениями, поведение векторов состояния и выхода определяется по формулам вида:
(2)
;
(3)
,
где Ф(t, ) - переходная матрица, или матрица Коши, являющаяся решением уравнения
(4)
,
с начальным условием Ф(τ,τ)=I.
Первые слагаемые в выражениях (2), (3) описывают свободное движение, а вторые - вынужденное. Для многомерных стационарных систем, описываемых уравнениями (1), законы изменения вектора состояния и вектора выхода находятся по следующим формулам:
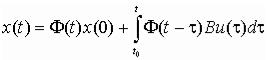 ,
,
,
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
78 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
где Ф(t-τ) - переходная матрица стационарной системы, зависящая от разности t- . В данном случае решение уравнения (4) имеет вид
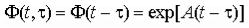 .
.
Одними из важнейших задач теории управления является исследование управляемости и наблюдаемости динамических систем. Сформулируем соответствующие определения и критерии для стационарных линейных систем.
Система называется вполне управляемой, если выбором управляющего воздействия u(t) на интервале времени [t0B ,B t1B B] можно перевести систему из любого начального состояния х(t0B )B в произвольное заранее заданное конечное состояние x(t1B )B .
Система называется вполне наблюдаемой, если по реакции у(t1B )B на выходе системы на интервале времени [t0B ,B t1B B] при заданном управляющем воздействии u(t) можно определить начальное состояние х(t0B )B .
Критерий управляемости линейных систем. Для того чтобы система была вполне управляемой, необходимо и достаточно, чтобы ранг матрицы
управляемости
MUB B =(В АВ А2P PВ … АnP -1ВP )
равнялся размерности вектора состояния: rang MUB =B n.
Критерий наблюдаемости линейных систем. Для того чтобы система была вполне наблюдаемой, необходимо и достаточно, чтобы ранг матрицы наблюдаемости
MYB B =(CTP P APTCP TP P (ATP )P 2P PC … (APT)P nP -1CP TP )P
равнялся размерности вектора состояния: rang MYB =B n.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
79 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Использование Control System Toolbox
Для решения задачи используется пакет прикладных программ Control System Toolbox среды MatLab. В Control System Toolbox имеется тип данных,
определяющих динамическую систему в пространстве состояний. Синтаксис команды, создающий непрерывную LTI (Linear Time Invariant)-систему в виде ss-объекта с одним входом и одним выходом: SS(A, B, C, D).
В эту функцию в качестве параметров передаются матрицы уравнений состояний и выходов вида:
в связи с тем, что рассматривается модель вида (1), то матрица динамики D будет нулевой.
Для выполнения работы могут применяться команды, приведенные в табл.1. Таблица 1. Некоторые команды Control System Toolbox
Синтаксис |
Описание |
ctrb(LTI-объект>) ctrb(A, B) |
Формирование матрицы |
|
управляемости |
obsv(<LTI-объект>) obsv(A, C) |
Формирование матрицы |
|
наблюдаемости |
Parallel(<LTI1>,<LTI2>) |
Параллельное соединение |
series(<LTI1>,<LTI2>) |
Последовательное соединение |
feedback(<LTI1>,<LTI2>) |
Соединение обратной связью |
append(<LTI1>, …, <LTIN>) |
Объединение систем |
connect(<sys>,<Con>,<in>,<out>) |
Установление связей в соединении |
Для получения результатов вычисления матриц, результирующей системы, по структурной схеме, воспользуемся последними двумя командами.
Функция append создает объект sys, представляющий собой объединение всех подсистем. При этом первый входной сигнал первой системы становится входом номер 1, второй входной сигнал первой системы - номер 2, и т.д. далее идут входы второй системы, и т.д.; аналогично определяются и выходы.
В функции connect - параметр <Con> определяет матрицу связей по структурной схеме. Матрица формируется по следующему правилу: каждая строка представляет собой один вход системы sys, первый элемент - номер входа (в соответствии с порядком в команде append), затем идут номера выходов, которые суммируются и подаются на рассматриваемый вход. Параметры <in>, <out> - строки из номеров входов и выходов соединения, являющиеся внешними.
Например, для последовательного соединения двух систем (см. рис.2б): sys1= ss(A1, B1, C1, 0)
sys2= ss(A2, B2, C2, 0) sys=append (sys1, sys2)
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
80 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
sysc=connect(sys, [2 1], [1], [2])
В этом случае на вход второй системы (общий вход номер 2), поступает выход первой (общий выход номер 1); вход первой системы (номер один) и выход второй системы (номер два) являются внешними.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
81 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Задание к лабораторной работе.
Даны три линейные стационарные системы:
1. 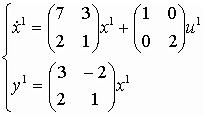 ;
;
2. 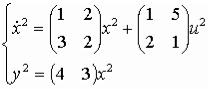 ;
;
3.  ;
;
и структурная схема соединения систем:
1. Приведем систему №3 к матричному виду, для этого введем переменные:
 ;
;
и, подставляя их в исходные уравнения, получим - |
|
||
|
; |
; |
. |
2. Создадим матрицы первой системы - |
|
|
|
>> A1=[7 3;2 1] |
|
|
|
B1=[1 0; 0 2] |
|
|
|
C1=[3 -2; 2 1] |
|
|
|
A1 = |
|
|
|
7 |
3 |
|
|
2 |
1 |
|
|
B1 = |
|
|
|
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
82 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
1 |
0 |
0 |
2 |
C1 = |
|
3 |
-2 |
2 |
1 |
Создавая, аналогично, матрицы двух других систем создадим ss-объекты:
>>A2=[1 2;3 2];
>>B2=[1 5; 2 1];
>>C2=[4 3];
>>A3=[0 1;2 3];
>>B3=[0; 4];
>>C3=[1 0];
>>s1=ss(A1, B1, C1,0)
a =
|
x1 |
x2 |
x1 |
7 |
3 |
x2 |
2 |
1 |
b = |
u1 |
u2 |
|
||
x1 |
1 |
0 |
x2 |
0 |
2 |
c = |
x1 |
x2 |
|
||
y1 |
3 |
-2 |
y2 |
2 |
1 |
d = |
u1 |
u2 |
|
||
y1 |
0 |
0 |
y2 |
0 |
0 |
Continuous-time model. >> s2=ss(A2, B2, C2,0)
a = |
x1 |
x2 |
|
||
x1 |
1 |
2 |
x2 |
3 |
2 |
b = |
u1 |
u2 |
|
||
x1 |
1 |
5 |
x2 |
2 |
1 |
c = |
x1 |
x2 |
|
||
y1 |
4 |
3 |
d = |
u1 |
u2 |
|
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
83 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
y1 0 0 Continuous-time model. >> s3=ss(A3, B3, C3,0) a =
x1 |
|
x2 |
x1 |
0 |
1 |
x2 |
2 |
3 |
b = |
|
|
u1 |
|
|
x1 |
0 |
|
x2 |
4 |
|
c = |
|
|
x1 |
|
x2 |
y1 |
1 |
0 |
d = |
|
|
u1 |
|
|
y1 0 Continuous-time model.
3.Исследуем наблюдаемость и управляемость каждой системы, для чего построим соответствующие матрицы и посчитаем их ранги -
>> rank(obsv(A1,C1)) ans =
2
>> rank(ctrb(A2,B2)) ans =
2
>> rank(obsv(A2,C2)) ans =
2
>> rank(ctrb(A3,B3)) ans =
2
>> rank(obsv(A3,C3)) ans =
2
Видно, что во всех случаях ранги матриц управляемости и наблюдаемости совпадают с размерностями пространства состояний.
4.Получим систему, определяемую соединением.
Для корректного использования функции connect введем дополнительную систему, передаточная функция которой равна 1.
>> s4 = tf(1) Transfer function:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
84 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
1
>>sys=append(s1,s2,s3,s4);
>>Q=[2 -4 5; 3 1 0; 4 2 0; 5 2 0];
>>in=[1 5];
>>out=[3 4];
>>s_com=connect(sys,Q, in,out);
Обращаясь к данным объекта, можно получить матрицы А, В, С:
>>A=s_com.A;
>>B=s_com.B;
>>C=s_com.C;
5.Вычислим ранги матриц наблюдаемости и управляемости итоговой системы:
>> rank(ctrb(A,B)) ans =
6
>> rank(obsv(A,C)) ans =
6
Результаты показывают, что система управляема и наблюдаема.
6.Создать скрипт-файл:
1)загрузить данные с параметрами систем из ASCII файла;
2)выполнить соединение систем;
3)вычислить ранги матриц наблюдаемости и управляемости;
4)используя, оператор if else , сделать вывод на экран результатов оценки управляемости и наблюдаемости;
5)изменить входные данные систем и выполнить программу заново;
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
85 |
|
|
|
|
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №7 Тема: Синтез оптимального управления с полной обратной связью.
Краткие сведения из теории
Пусть поведение модели объекта управления описывается обыкновенным дифференциальным уравнением
x(t)=f(t,x(t),u(t)), (1)
где х - вектор состояния системы, х RPn,P RnP P - n-мерное евклидово пространство; u - вектор управления, и u U RnP ,P U - некоторое заданное множество допустимых значений управления, t T=[t0B ,B t1B B] - интервал времени функционирования системы, моменты начала процесса t0B B и окончания процесса t1B B заданы, f(t,x,u): ТxRnP xUP RnP .P
Задан функционал качества управления
(2)
где fP 0(P t,x,u), F(x) - заданные непрерывно дифференцируемые функции. Предполагается, что при управлении используется информация о текущем времени и векторе состояния х.
Применяемое в каждый момент времени t Т управление имеет вид управления c полной связью по всем переменным вектора состояния
(см. рис.1).
Рис.1. Схема управления с полной обратной связью по вектору состояния.
Требуется найти такую функцию u*(t, x) UnB B, что
. |
(3) |
|
Функция u*(t,x) UnB B называется оптимальным управлением с полной
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
86 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
обратной связью. Для любого начального состояния x0B B из множества RnP P она порождает соответствующую оптимальную пару, т.е. оптимальную траекторию х*(.P )P и оптимальное программное управление u*(.P )P .
Достаточным условием минимума функционала (2) является уравнение Беллмана для непрерывных детерминированных систем. Если существуют функция (t,x) C1,1P ,P удовлетворяющая уравнению Беллмана с граничным условием:
(4)
и управление u*(t,x) UnB ,B удовлетворяющее следующему условию:
то u*(t,x) является оптимальным управлением с полной обратной связью. При этом минимальное значение функционала (2)
 .
.
Пусть система, описывающая поведение модели объекта управления, является линейной
x (t)=A(t)x(t)+B(t)u(t) |
|
|
& |
(5) |
|
y(t)=C(t)x(t)+D(t)u(t) |
||
|
||
Пусть функционал качества управления квадратичный: |
|
|
|
(6) |
,
где S(t), - неотрицательно определенные симметрические матрицы размера (nx n), a Q(t) - положительно определенная симметрическая матрица (qxq).
Далее используем известные правила и обозначения :
Уравнение Беллмана для данной задачи имеет вид
(7)
.
Найдем максимум в последнем выражении по управлению с использованием необходимых условий экстремума и правила 1-3. Дифференцируя выражение в фигурных скобках по u и приравнивая результат нулю, получаем структуру оптимального управления:
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
87 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
(8)
Решение уравнения (7) ищется в виде
(9)
,
где K2B (B t) - неизвестная симметрическая матрица (nxn).
Подставляя (9) в уравнение (7), приравнивая нулю квадратичные формы, получаем:
(10)
.
Решая уравнение Риккати (10), можно получить явный вид оптимального управления (8) с полной обратной связью:
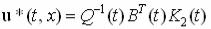 . (11)
. (11)
Минимальная величина функционала вычисляется по формуле
Рассмотрим дискретный случай |
. |
|
|
x(k+1)=A(k)x(k)+B(k)u(k); |
|
y(k)=C(k)x(k)+D(k)u(k); |
(12) |
k=0,1,…,N-1, |
|
с начальным условием |
|
x(0)=x0B ,B |
(13) |
и функционалом качества |
|
(14)
,
где Q(k), - неотрицательно определенные симметрические матрицы размера (nxn); R(k) - положительно определенная симметрическая матрица
(qxq).
Требуется найти управление u*(k, x) с полной обратной связью, минимизирующее функционал (14). Уравнение Беллмана принимают вид:
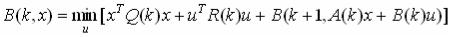 . (15)
. (15)
Функция Беллмана B(k,x) ищется в форме
B(k,x)=xTP P(k)x, (16)
где P(k) - где неизвестная неотрицательно определенная симметричная матрица (nxn).
Получаем, что в задаче (13)-(14) оптимальное управление определяется соотношением
u*(k,x)=-K(k)х, k=0,1,…,N-1,
где K(k) - матрица коэффициентов усиления регулятора размера (qxn):
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
88 |
|
|
|
|
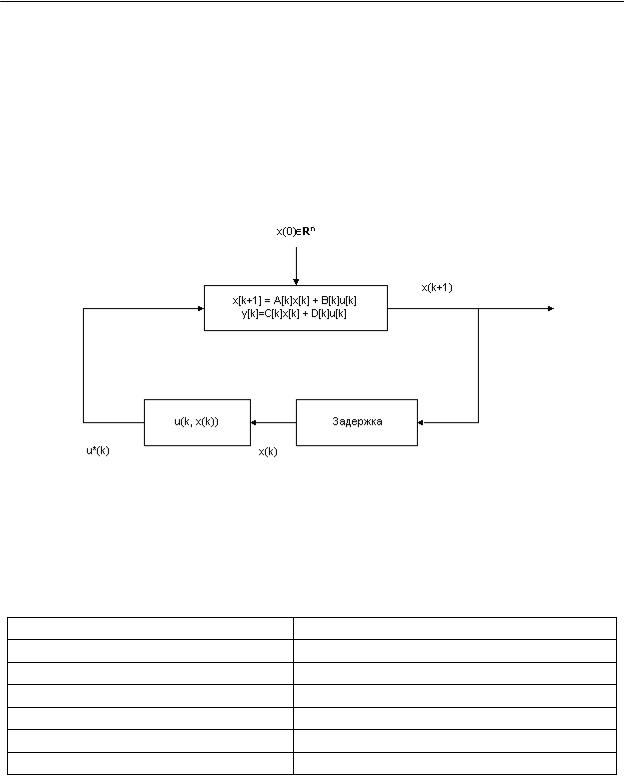
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
K(k) = [R(k) + BTP P(k+1)B(k)]-P 1PBTP (P k)P(k+1)A(k), k=0, l, ..., N-l,
а матрица P(k) размера (nxn) удовлетворяет уравнению:
P(k)=Q(k)+KTP (P k)R(k)K(k)+[A(k)-B(k)K(k)]TP P(k+l)[A(k)-B(k)K(k)], k=N-l,...,l,0,
P(N)= .
Для каждого начального состояния x0B B оптимальный линейный регулятор порождает оптимальное программное управление u*(x,k) и оптимальную траекторию х*(k). Структурная схема этой системы изображена на рис.2.
Рис.2. Схема регулирования.
Описание используемых функций
Для синтеза оптимального регуляторов линейных стационарных систем в Control System Toolbox имеются функции решений уравнений Беллмана
(см. табл.1).
|
Таблица 1. Функции Control System Toolbox |
Синтаксис |
Описание |
[K P e]=lqr(A,B,Q,S) |
Синтез непрерывного регулятора |
[K P e]=lqr(A,B,Q,S,N) |
Синтез непрерывного регулятора |
[K P e]=dlqr(A,B,Q,R) |
Синтез дискретного регулятора |
[K P e]=dlqr(A,B,Q,R,N) |
Синтез дискретного регулятора |
[K P e]=lqrd(A,B,Q,R,Ts) |
Синтез дискретного регулятора |
[K P e]=lqrd(A,B,Q,R,N,Ts) |
Синтез дискретного регулятора |
Функция lqr вычисляет матрицу коэффициентов регулирования K cо среднеквадратичным функционалом качества без терминального члена:
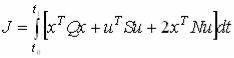 ,
,
при этом вычисляются матрица P, являющаяся решением уравнения Риккати и собственные значения e матрицы (A-BK).
Функция dlqr вычисляет матрицу коэффициентов регулирования по
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
89 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
всем переменным состояния K для дискретной системы со среднеквадратичным функционалом качества без терминального члена:
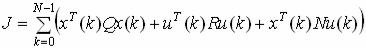 ,
,
при этом вычисляются матрица P, являющаяся решением уравнения Риккати и собственные значения e матрицы (A-BK).
Функция lqrd предназначена для синтеза оптимального дискретного регулятора непрерывной системы со среднеквадратичным функционалом качества:
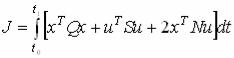 .
.
В качестве параметра в функцию передается шаг дискретизации Ts, возвращаются значения матрицы K дискретного управления, матрица P, являющаяся решением уравнения Риккати и собственные значения e матрицы системы управления, полученный в результате дискретизации.
При использованию всех команд синтеза оптимального линейного регулятора по всем переменным состояния на исходные данные накладываются следующие ограничения:
−система, определяемая матрицами (A, B) должна быть стабилизируема;
−должны выполняться неравенства S> 0, Q - NR-P 1PNTP >0;P
−пара матриц (Q - NR-P 1NP TP ,P A - BR-P 1PBTP )P не должна иметь наблюдаемые моды с собственными значениями на действительной оси.
Задание к лабораторной работе
Ниже приведен пример script-файла, моделирующего систему управления и синтез оптимального регулятора.
%Параметры системы
A=[1 0; -2 1]; B=[1 0; 1 0]';
%Параметры критериЯ качества управлениЯ
Q=[1/2 0;0 1/2]; R=[1/2 0; 0 1/2];
%ВремЯ регулированиЯ
T=100;
%Величина шаг
SS=0.5;
%Количество шагов
N=T/SS
%Вычисление параметров регулЯтора
[k p e]= dlqr(A, B, Q, R) x = zeros(2, N);
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
90 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
u= zeros(2, N-1);
%Начальные условиЯ x(1,1)=2;
x(2,1)=1;
%Построение графиков динамики системы for i=1:N-1,
u(:, i)= - k*x(:, i);,
x(:, i+1)=A*x(:, i)+B*u(:, i); end
x1= x(1,:); x2= x(2,:);
t = 0:SS:T-SS; subplot(4, 1, 1); plot(t, x1, 'b'); subplot(4, 1, 2); plot(t, x2, 'g'); subplot(4, 1, 3);
plot(SS:SS:T-SS, u(1, :), 'y'); subplot(4, 1, 4); plot(SS:SS:T-SS, u(2, :), 'r');
Результаты вычисления следующие: значения параметров оптимального регулятора -
k =
0.8229 -0.1771
0.8229 -0.1771 p =
3.7343 -1.4114 -1.4114 1.1614
e =
0.1771 + 0.1771i
0.1771 - 0.1771i
Графики динамики системы представлены на рис.3.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
91 |
|
|
|
|
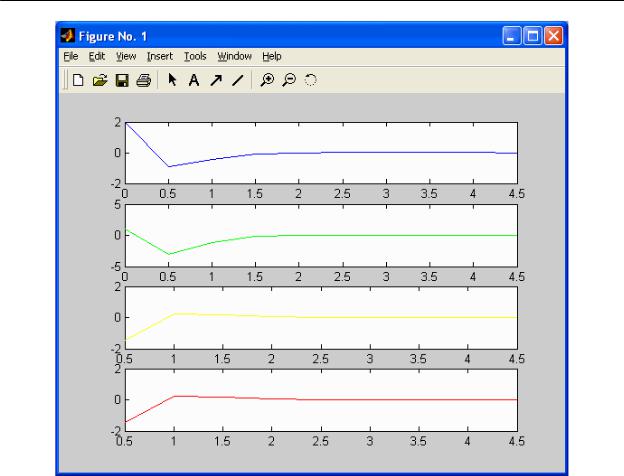
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рис.3. Динамика состояний и управлений: x1B ,B x2B ,B u1B ,B u2B .B
На рис.4-5 показан другой пример синтеза оптимального линейного регулятора.
Оформить результаты в виде отчета.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
92 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рис.4. Динамика состояний и управлений: u1B (B k).
Рис.5. Динамика состояний и управлений: u2B (B k).
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
93 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Лабораторная работа №8 Тема: Устойчивость линейных систем
Краткие сведения из теории |
|
Рассмотрим линейную систему |
(1) |
. |
Система управления называется устойчивой по Ляпунову, если при ненулевых ограниченных начальных условиях свободное движение ограничено.
Согласно определению, динамическая система асимптотически устойчива, если для любого начального состояния x(0)=x0B B, ее решение х(t,x0B )B стремится к нулю по норме, при t .
Существует большое количество критериев, являющихся достаточным условием устойчивости. Для линейных систем устойчивость системы являются асимптотически устойчивыми.
Мощным инструментом исследования устойчивости динамических систем является метод функций Ляпунова. Для линейных автономных систем существование функции Ляпунова в виде квадратичной формы является одновременно необходимым и достаточным условием равномерной асимптотической устойчивости в целом.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
94 |
|
|
|
|
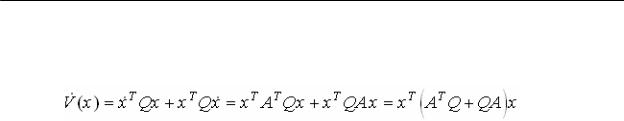
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рассмотрим линейную стационарную систему. Допустим, что нам удалось найти функцию Ляпунова: V(x)=xTP QxP , где Q - симметричная и положительная определенная матрица. Тогда запишем:
|
|
. |
(2) |
Обозначим |
|
|
|
|
|
|
|
T |
Q+QA=-C, |
|
(3) |
AP |
|
||
|
P |
|
|
тогда, поскольку С положительно определенна, то система асимптотически устойчива в целом. Более того, т.к. имеет место:
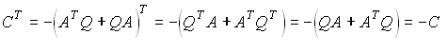 ,
,
то матрица С симметрична.
На практике целесообразно решать обратную задачу. Выбирают какуюлибо положительно определенную положительную матрицу, например C = I. Тогда из (3) можно получить Q. Если квадратичная форма Q оказывается неопределенной (знакопеременной), то по теореме Ляпунова о неустойчивости начало координат неустойчиво. Если Q положительно определена, то поскольку система линейна и стационарна, начало координат асимптотически устойчиво в целом. Обоснованность такого анализа зависит от того, определяет ли уравнение (3) однозначно матрицу Q, если задана симметричная и положительная С.
Справедливы следующие утверждения:
1.Если n собственных значений 1B ,B …, nB B матрицы A таковы, чтоiB +B jB B 0 (i,j=1,2,…,n), то из уравнения (3) при заданной матрице С матрица Q определяется однозначно. (Достаточное условие устойчивости матрицы А).
2.Если матрица А устойчива и матрица С положительно определена, то матрица Q также положительно определена. (Необходимое условие устойчивости матрицы А).
Рассмотрим, например дискретную управляемую систему, описываемую конечно-разностными уравнениями в пространстве состояний
x(k+1)=A(k)x(k)+B(k)u(k), k=(0,N),
и, пусть известна матрица K, определяющая закон управления u=Kx. Требуется определить асимптотическую устойчивость систему с полной обратной связью.
Система асимптотически устойчива в том и только том случае, если решение Г, являющееся (nх n)-матрицей, уравнения Ляпунова
T |
|
Г(A+BL)-Г=-H, |
(4) |
(A+BL)P |
P |
является положительно-определенной матрицей. Здесь H - произвольная положительно-определенная симметричная матрица. Для определенности в уравнении (4) матрицу H можно положить единичной.
Для установления положительной определенности симметричной матрицы Г можно воспользоваться критерием Сильвестра: iB >0B для i=(1,n), где iB B - миноры i-го порядка матрицы Г.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
95 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Описание используемых функций
Для определения асимптотической устойчивости линейных стационарных систем в Control System Toolbox имеются функции вычисления решений уравнений Ляпунова, представленные в табл.1.
Таблица 1. Функции Control System Toolbox
Синтаксис |
Описание |
Q = lyap(A, C) |
Решение непрерывных уравнений Ляпунова |
Q = lyap(A, X, Y) |
Решение непрерывных обобщенных уравнений |
|
Ляпунова (уравнений Сильвестра) |
Г = dlyap(A, H) |
Решение дискретных уравнений Ляпунова |
Функция
Q=lyap(A,С)
находит решение системы уравнений Ляпунова вида (3). Функция
Q=lyap(A,X,Y)
находит решение уравнений Сильвестра (обобщенных уравнений Ляпунова) вида:
AГ+ГX-Y=0.
Функции решения непрерывных уравнений Ляпунова выдают результат только в случае единственности решения, т.е. в случае, когда собственные значения λ11,...,λ1n матрицы A и собственные значения λ21,...,λ2n матрицы X для всех (i,j) удовлетворяют условию λ1i +λ2j ≠ 0 .
Функция Г=dlyap(A,H)
находит решение системы уравнений Ляпунова вида (4). Результат решения уравнений Ляпунова для дискретных систем выдается только в случае единственности решения, т.е., когда собственные значения λ1B ,B …,λBnB матрицы A для всех (i,j) удовлетворяют условию λiB λB jB ≠B 1.
Задание к лабораторной работе
Задана система управления, описываемая конечно-разностными уравнениями в пространстве состояний
x(k+1)=A(k)x(k)+B(k)u(k), k=(0,N),
и известна матрица K, определяющая закон управления u=Kx, 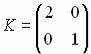 .
.
1. Зададим матрицы, определяющие систему:
>> A=[1 2; -3 4]
A=
1 2
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
96 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
-3 4
>>B= [1 2]' B =
1
2
>>L=[2 1] L =
2 1
2. Определим решение уравнения Ляпунова
>>G=dlyap(A, eye(2))
G=
-0.2211 -0.1215 -0.1215 -0.1285
3. Произведем расчет главных миноров
>>det(G(1:1, 1:1)) ans =
-0.2211
>>det(G)
ans = 0.0136
По критерию Сильвестра решение не является положительноопределенной матрицей, следовательно, система не является асимптотически устойчивой. График свободного движения системы при начальных условиях x=(x1B ,xB 2B )=(2,1)B показан на рис.1 и 2.
4. Аналогично можно определить свойство асимптотической устойчивости в управляемой системе
>> G=dlyap(A+B*L, eye(2)) G =
-0.2563 0.0833 0.0833 -0.0498
>>det(G) ans =
0.0058
>>det(G(1:1, 1:1)) ans =
-0.2563
По критерию Сильвестра решение дискретного уравнения Ляпунова не является положительно-определенной матрицей, следовательно, система не является асимптотически устойчивой. График динамики управляемой
системы при начальных условиях x=(x1B ,xB 2B )=(2,1)B показан на рис.3 и 4 соответственно.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
97 |
|
|
|
|
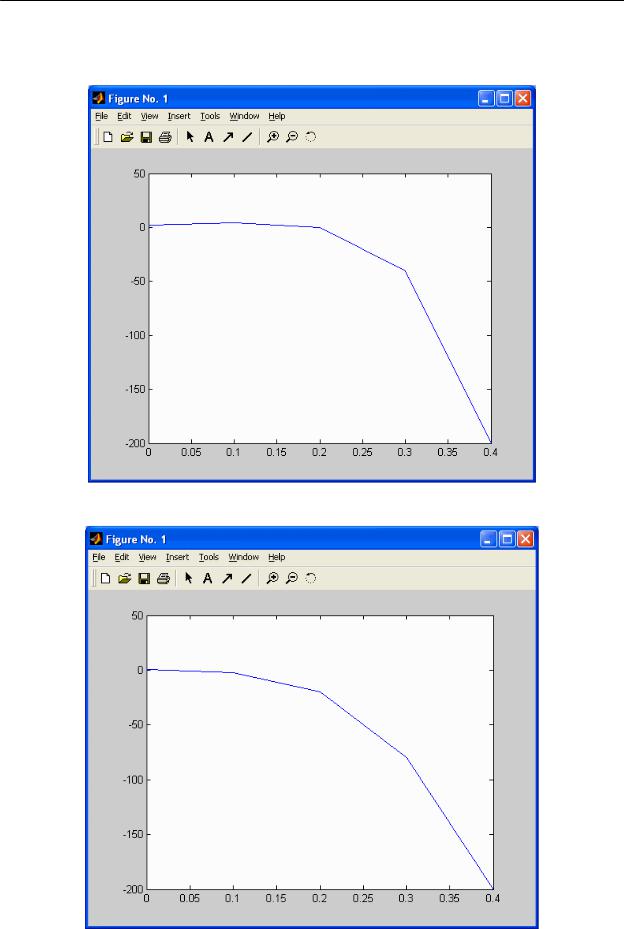
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Оформить результаты работы в виде отчёта.
Рис.1. График свободного движения системы x1B (B k).
Рис.2. График свободного движения системы x2B (B k).
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
98 |
|
|
|
|
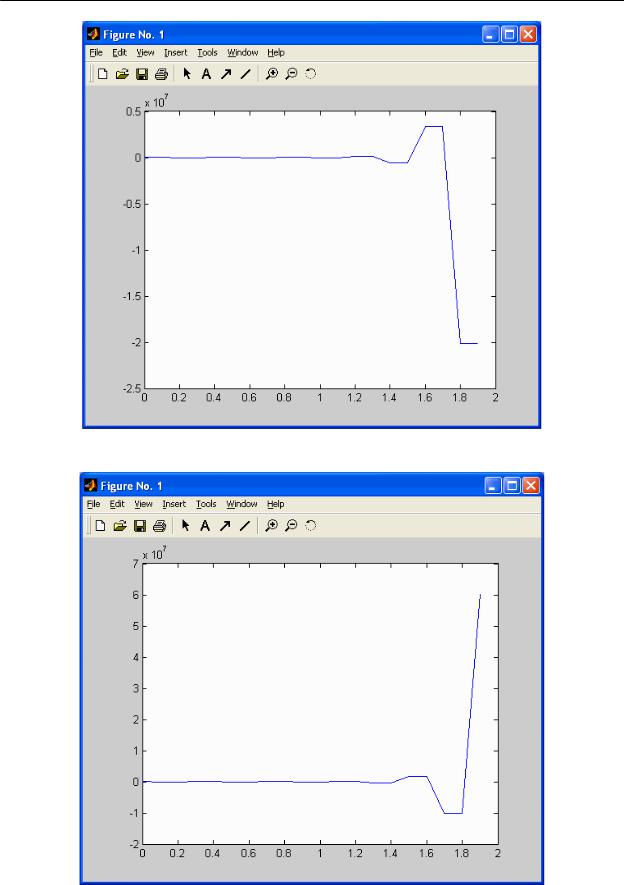
Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Рис.3. График свободного движения системы x1B (B k).
Рис.4. График свободного движения системы x2B (B k).
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
99 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Приложение 1
1. Основные понятия и определения теории автоматического управления и регулирования
Управление - есть формирование управляющих воздействий обеспечивающих требуемый режим работы объекта управления. Регулирование - это частный вид управления, когда задачей является обеспечение постоянства какой-либо выходной величины (координаты объекта управления).
Автоматическое управление - управление, осуществляемое без непосредственного участия человека.
Объект управления (ОУ) - устройство, требуемый режим работы которого, должен поддерживаться из вне специально организованными управляющими воздействиями.
Управляющее устройство (УУ) - устройство осуществляющее воздействие на объект управления с целью обеспечения требуемого режима работы. Управляемые координаты - величины, характеризующие состояние объекта управления.
Возмущениями называются воздействия, вызывающие отклонения координат от заданного закона управления и не зависящие от управляющего устройства.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
100 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Система автоматического управления (САУ) - система, состоящая из объекта управления и устройства управления, в которой автоматически выполняется заданный процесс.
Линейные стационарные САУ - системы с постоянными параметрами, описывающиеся линейными дифференциальными уравнениями с постоянными коэффициентами.
САУ разомкнутые — системы в которых заданное значение выходной величины ОУ достигается при помощи регулирующего (исполнительного) органа, устанавливаемого в определенное положение.
САУ замкнутые - системы в которых заданное значение выходной величины сравнивается с ее текущим значением, поступающим через элемент обратной связи на специальный элемент сравнения, который вырабатывает сигнал ошибки САУ. Усиленный сигнал ошибки приводит в движение регулирующий орган ОУ.
Система - совокупность взаимосвязанных элементов, совместно достигающих целевого или равновесного состояния.
С понятием системы связаны понятия состояния системы, входа и выхода системы.
Состояние динамической системы описывается совокупностью физических переменных x1B B(t), ..., xnB B(t), характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.
Вектор состояния системы  (t) это векторная переменная, содержащая переменные состояния динамической системы, позволяющая однозначно определить выход Y(t) системы через ее вход U(t) и начальное состояние x(tB0)B .
(t) это векторная переменная, содержащая переменные состояния динамической системы, позволяющая однозначно определить выход Y(t) системы через ее вход U(t) и начальное состояние x(tB0)B .
Переменными состояния динамической системы xiB (t),B i = l, 2, ..., n
называют такие независимые переменные, набор которых достаточен для полного математического описания состояния системы в динамике. Количество переменных состояния для полного математического описания системы должно быть равно количеству динамических звеньев этой системы. Вход системы u(t) - точка приложения рассматриваемого воздействия, представляет внешние переменные, действующие на систему. Выражается множеством временных функций или множеством временных последовательностей входных значений. Количество входных воздействий принято обозначать т.
Выход системы y(t) - точка где наблюдается эффект вызванный входным воздействием, представляет описание непосредственно наблюдаемого поведения системы. Выражается аналогично входу. Количество выходных переменных принято обозначать r.
Порядок системы n зависит от числа переменных состояния, и равен числу динамических звеньев рассматриваемой системы.
Пространством состояний называется пространство X, к которому принадлежит вектор переменных состояния рассматриваемой системы  (t)
(t)
X.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
101 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
Передаточная функция САУ (ПФ) - есть отношение преобразования Лапласа от выходной величины к преобразованию Лапласа от входной величины при нулевых начальных условиях.
Структурная схема - условное графическое изображение системы. Устойчивость - это свойство САУ возвращаться в заданный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
Изменения во времени входных воздействий и выходных величин объекта управления характеризуют его поведение, его действие.
Входные воздействия, с точки зрения их влияния на действие объекта, на его выходные величины, разделяются на две принципиально отличные группы. Некоторые из входных воздействий обеспечивают, как уже отмечалось, желаемое изменение поведения объекта, достижение поставленных целей. Такие входные воздействия называют управляющими, и при их отсутствии задача управления вообще не имеет решения. Эти воздействия осуществляет управляющее устройство.
Другие входные воздействия, напротив, мешают достижению цели, и изменить их, как правило, невозможно. Такие воздействия называют возмущающими (возмущениями) или помехами. Помехи связаны с побочными явлениями, и всякое уменьшение их улучшает работу ОУ.
Задача управления, по существу, заключается в формировании такого закона изменения управляющих воздействий, при котором достигается желаемое поведение объекта независимо от наличия возмущений.
Сложная и разносторонняя задача управления в подавляющем большинстве случаев включает более узкую задачу регулирования. Задача регулирования заключается в поддержании выходных величин объекта равными (или пропорциональными) некоторым эталонным функциям времени - задающим воздействиям. Последние могут быть постоянными или изменяющимися как по заданному, так и по заранее неизвестному закону.
Воздействия, несущие в себе информацию необходимую для процесса управления называются задающими воздействиями.
Воздействия УУ на ОУ называются управляющими воздействиями.
2. Передаточная функция линейной непрерывной стационарной системы и ее свойства
В теории автоматического управления широкое применение получил способ математического описания, основанный на понятии передаточной функции. Для расчетов обычно необходима ПФ разомкнутой САУ, а также ПФ замкнутой САУ относительно задающего воздействия, возмущения, ошибки и т.д.
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
102 |
|
|
|
|

Методические указания к курсу лабораторных работ по дисциплине “Основы ТАУ”
направление 6.091500 “Компьютерная инженерия”
В общем случае, для одномерной системы, математическое описание системы или объекта в виде передаточной функции есть отношение двух полиномов.
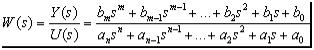 , (1)
, (1)
где s - оператор Лапласа.
ПФ для разомкнутых САУ обозначается W(s). Для замкнутых САУ ПФ принято обозначать Ф(s) с указанием воздействия относительно которого она определена. Например, ФyuB B(s) - передаточная функция замкнутой САУ по управлению.
При этом корни полинома числителя Y(s) в (1) называются нулями передаточной функции, а корни полинома знаменателя U(s) являются полюсами передаточной функции.
Удобно использовать передаточную функцию в виде отношения двух нормированных полиномов (т.е. полиномов у которых коэффициент при младшем члене равен 1), умноженных на постоянный коэффициент k - называемый передаточным коэффициентом звена или системы, реже коэффициентом усиления.
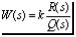 . (2)
. (2)
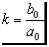 (3)
(3)
Размерность передаточного коэффициента равна размерности выходной величины, деленной на размерность входной величины.
Формой описания процессов в многомерных линейных стационарных системах является передаточная матрица. В общем случае передаточная матрица имеет вид
 ; (4)
; (4)
где: wijB B(s) - элементы передаточной матрицы, дробно-рациональные функции, являющиеся частными передаточными функциями многомерной САУ, связывающими между собой i-ый выход и j-ый вход объекта управления.
Элементы расположенные на главной диагонали такой матрицы являются частными передаточными функциями прямых связей, остальные частные передаточные функции перекрестных связей.
Общим свойством для элементов передаточной матрицы является то, что все
они имеют одинаковый знаменатель. f(s) = a0B B + a1B sB + a2B sB 2P P + ...+ anB sB nP .P (5)
Характеристическим полиномом системы f(s) называется знаменатель передаточной функции (1). Характеристический полином приравняный к нулю называется характеристическим уравнением. Корни выражения f(s) = 0 являются характеристическими числами (полюсами) динамической системы,
обновление от 16.02.2004
|
|
|
ЧДТУ 2004 |
103 |
|
|
|
|
