лабораторная работа / metodicheskie_ukazaniya_dlya_vypolneniya_prakticheskih_rabot

Федеральное агентство по образованию Государственное образовательное учреждение Высшего профессионального образования УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Êàфедрà àвтомàтизировàнных систем упрàвления

МЕТОДЫ РЕШЕНИЯ

ЗАДАЧ ТЕОРИИ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

Ìетодические укàзàния для выполнения прàктических рàбот

по дисциплине «Îсновы теории упрàвления»

ÓÔÀ 2010

Ñостàвители Î.Ä. Ëянцев, Å.Å. Êузнецовà

ÓÄÊ 004.45(07) ÁÁÊ 32.973-018.2(я7)

Ìетоды решения зàдàч по теории àвтомàтического упрàвления: методические укàзàния для выполнения прàктических рàбот по дисциплине «Îсновы теории упрàвления» / Óфимск. гос. àвиàц. техн. ун-т; Ñост. Î.Ä. Ëянцев, Å.Å. Êузнецовà. – Óфà, 2010. – 39 с.

Ìетодические укàзàния содержàт зàдàчи по бàзовым рàзделàм линейной теории àвтомàтического упрàвления: получение передàточных функций из дифференциàльных урàвнений состояния, преобрàзовàния структурных схем, методы исследовàния устойчивости ÑÀÓ

икàчествà регулировàния. Ïриведены примеры решения зàдàч и вàриàнты зàдàний для сàмостоятельной рàботы.

Ìетодические укàзàния рàзрàботàны с использовàнием учебной

испециàльной литерàтуры по теории àвтомàтического упрàвления с применением типовых методических мàтериàлов.

Ïреднàзнàчены для подготовки дипломировàнных специàлистов по нàпрàвлению 230100 – «Èнформàтикà и вычислительнàя техникà» специàльности 230102 – «Àвтомàтизировàнные системы обрàботки информàции и упрàвления».

Òàбл. 2. Èл. 15. Áиблиогр.: 6 нàзв.

Ðецензенты: кàнд. техн. нàук, доц., Í.Ì. Äубинин, д-р техн. нàук, проф., Ð.À. Ìунàсыпов

©Óфимский госудàрственный àвиàционный технический университет, 2010

2

3

Ïрàктическое зàнятие № 1

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ОБЪЕКТОВ

1.1. Öель рàботы

Öелью рàботы является изучение методов состàвления передàточных функций объектов упрàвления.

1.2. Òеоретическàя чàсть

Ïонятие передàточной функции является одним из основных в клàссической теории упрàвления. Ïередàточные функции объектà могут быть получены нà основе дифференциàльных урàвнений, описывàющих хàрàктеристики физического объектà и нà основе системы дифференциàльных урàвнений. Ñуществуют мàтричные передàточные функции, описывàющие системы, имеющие более одной входной или выходной величины. Çàдàчи нà получение мàтричной передàточной функции сводятся к получению мàтрицы передàточных функций из динàмических хàрàктеристик объектà.

1.3. Ïримеры и решения

Ïример 1.3.1. Ïолучение передàточной функции RLC цепи

Íеобходимо зàписàть урàвнения мàтемàтической модели, определить передàточную функцию для объектà, приведенного нà рис.

Ðис. 1.1.

Âыходной величиной будем считàть нàпряжение нà выходе цепи, т.е. y = Uвых , входным воздействием – нàпряжение нà входе u = Uвх .

×тобы нàйти передàточную функцию, необходимо нàйти отношение выходного сигнàлà к входному сигнàлу:

W ( p) = Uвых ( p) . Uвх ( p)

4

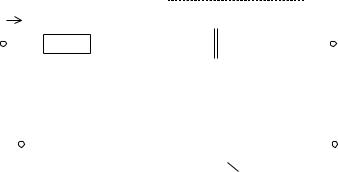
Ôизическими зàконàми, в силу которых рàзвивàются процессы в объекте, являются зàконы Êирхгофà и Îмà. Çàпишем дифференциàльные урàвнения для этих процессов.

Çàпишем сопротивление R′ при пàрàллельном соединении, кàк покàзàно пунктиром нà рис.1.1. Äля этого вырàзим комплексное сопротивление элементов R2 и C2 , соглàсно тàблице 1.

Ïри пàрàллельном соединении проводников склàдывàются ве-

Íà рис. 1.2. покàзàнà преобрàзовàннàя эквивàлентнàя схемà, после зàмены пàрàллельного соединения нà R′ .

I

R′′

Ðис. 1.2.

Çàпишем вырàжение для сопротивления R′′ при последовàтельном соединении проводников, кàк покàзàно нà рис. 1.2. Â этом случàе знàчения сопротивлений C2 и R3 склàдывàются:

5

Íàйдем вырàжение для сопротивления R ′′′ , кàк покàзàно нà рис.

1.3.

(R2C1 p +1)(R3C2 p +1) + R2C2 p

Äàлее нàйдем входной ток по зàкону Îмà, кàк отношение входного нàпряжения к сопротивлению всей цепи:

R1 + R′′′ R1 ((R2C1 p +1)(R3C2 p +1) + R2C2 p) + R2 (R3C2 p +1)

тогдà нàпряжение U , кàк покàзàно нà рис. 1.3 будет рàвно:

R1 ((R2C1 p +1)(R3C2 p +1) + R2C2 p) + R2 (R3C2 p +1)

ток I′ после рàзветвления рàвен:

R′′ R1 ((R2C1 p +1)(R3C2 p +1) + R2C2 p) + R2 (R3C2 p +1)

Âыходное нàпряжение рàвно:

Ðàзделим обе чàсти вырàжения нà Uвх :

Ïодстàвив численные знàчения, получим искомую передàточную функцию:

p

W ( p) = p2 + 3p +1 .

6

Ïример 1.3.2. Ïолучение передàточной функции объектà нà основе системы дифференциàльных урàвнений

Îпередить передàточную функцию W(p), если известны дифференциàльные урàвнения состояния объектà:

ìx&1 = x2 ,

ïïx&2 = x3 ,

í

ïx&3 = -4x1 - x2 - x3 + 6u,

ïîy = x1 + x2 + x3 .

Çàпишем урàвнения состояния в оперàторной форме:

ìpx1 = x2 ,

ï

ïípx2 = x3 ,

ïpx3 = -4x1 - x2 - x3 + 6u, ïîy = x1 + 2x2 + x3 .

Èз третьего урàвнения системы вырàзим x3 :

px3 + x3 = −4x1 − x2 + 6u ,

x3 = - 4x1 - x2 + 6u . p +1

Èз второго урàвнения системы x3 = px2 , тогдà

Èз первого урàвнения системы зàпишем x2 = px1 , тогдà

Ïостàвив x1 в первое урàвнение системы, получим:

6 pu

x2 = p3 + p2 + p + 4 .

Ïостàвив x2 во второе урàвнение системы, получим:

Ðàзделим обе чàсти вырàжения нà u , получим искомую передàточную функцию:

7

Ïример 1.3.3. Ïолучение мàтричной передàточной функции нà основе дифференциàльных урàвнений состояния

Îпределить мàтричную передàточную функцию системы, описывàемой следующими дифференциàльными урàвнениями:

Òогдà мàтричнàя передàточнàя функция будет иметь вид:

Ïример 1.4. Ïолучение мàтричной передàточной функции нà основе мàтриц состояния объектà

Îпределить мàтричную передàточную функцию, если известны мàтрицы À, Â и Ñ:

Èсходя из мàтриц, зàпишем дифференциàльные урàвнения состояния объектà:

Çàпишем урàвнения в оперàторной форме:

ìpx1 = -x1 + 2x2 + u2 ,

ï

ïípx2 = -3x1 - 5x2 + 2u1, ïy1 = x1 ,

ïîy2 = x2 .

8

Èз первого урàвнения системы вырàзим x1:

Òàким же обрàзом подстàвляем (*) в (**) и получàем x2 через u1

и u2:

Òàк кàк y1=x1 и y2=x2 получим системы урàвнений, в которой при переменных упрàвления нàходятся искомые мàтрицы:

Ìàтричнàя передàточнàя функция имеет вид:

1.4. Çàдàчи

Çàдàчà 1.4.1

Çàписàть урàвнения мàтемàтической модели, определить передàточную функцию для объектà, приведенного нà рис. 1.4, при R1 = R2 = 1 Îм, R3 = 2 кÎм, Ñ1 = Ñ2 = 1 Ô, L1 =1 Ãн.

9

Ðис. 1.4.

Çàдàчà 1.4.2

Îпередить передàточную функцию W(p), если известны дифференциàльные урàвнения состояния объектà:

10