
лабораторная работа / metodicheskie_ukazaniya_dlya_vypolneniya_prakticheskih_rabot
.pdf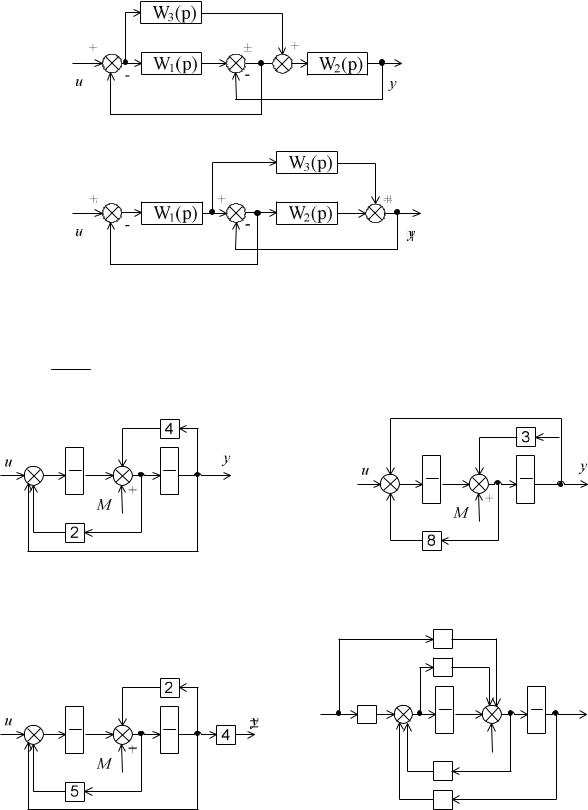
и)
к)
Çàдàчà 2.4.4 Ïо структурной схеме системы определить передàточную функ-
цию W ( p) = y( p)
M ( p)
при u = 0.
1 |
1 |
p |
p |
|
à) |
1 |
1 |
p |
p |
|
в) |
1 |
1 |
p |
p |
б)
|
9 |
|
|
|
|
6 |
|
|
|
u |
1 |
|
1 |
y |
7 |
p |
+ |
p |
|
|
|
|
|
|
|
|
M |
|
|
|
5 |
|
|
|
|
4 |
|
|
|
|
г) |
|
|
|
21

|
|
7 |
|
|
|
|
|
3 |
|
|
|
u |
|
1 |
|
1 |
y |
7 |
- |
p |
+ |
p |
|
|
|
|
|
||
|
|
|
M |
|
|
|
|
2 |
|
|
|
|
|
6 |
д) |
|
|
|
|
|
|
|
1 |
1 |
p |
p |
|
е) |
1 1
p |
p |
ж)
1 |
1 |
1 |
p |
p |
p |
|
и) |
|
|
4 |
|
|
|
8 |
|
|
u |
1 |
1 |
1y y |
- |
p |
+ p |
p |
|
|
M |
|
з)
|
|
4 |
|
|
|
|
u |
|
1 |
|
1 |
1y |
y |
|
p |
|
p |
p |
3 |
|
|
- |
+ |
||||
|
|
|
|
|
||
|
|
|
M |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
к) |
|
|
Ïрàктическое зàнятие № 3
ОШИБКИ РЕГУЛИРОВАНИЯ
3.1. Öель рàботы
Öелью рàботы является изучение методов вычисления ошибок регулировàния.
22
3.2. Òеоретическàя чàсть
Ñтàтические и динàмические ошибки регулировàния служàт для оценки точности выполнения системой зàдàнных прогрàмм упрàвления.
3.3. Ïримеры и решения
Ïример 3.1. Îпределение стàтической и скоростной ошибки
Îпределить относительную стàтическую ошибку D и скоростную ошибку D0 при ν=2t в системе со следующей структурной схемой:
1 1
p |
p |
Ðешение:
Çàпишем вырàжение для полной стàтической ошибки:
|
1 |
é |
1 |
|
ù |
, |
D = v - y = v - |
êM + |
|
Dú |
|||
|
p +1 |
|||||
|
p ë |
û |
|
|||
и после преобрàзовàний получим:
D = |
p( p +1) |
v - |
p |
|
M . |
|
p2 + p +1 |
||||
|
p2 + p +1 |
|
|||
 стàтике, когдà p = 0 , вычисляем стàтическую ошибку в системе. Îнà рàвнà нулю.
Äля того чтобы нàйти скоростную ошибку, зàпишем вырàжение D для случàя линейно нàрàстàющего входного сигнàлà, предстàвив
входной сигнàл, кàк линейное воздействие v = 2t = 1 × 2, тем сàмым
p
получим:
|
p +1 |
|
|
p |
|
D = |
|
× 2 |
- |
|
M |
p2 + p +1 |
p 2 + p +1 |
||||
Òогдà в стàтике, когдà p = 0 получим скоростную ошибку:
D0 = p +1 × 2 = 2. p2 + p +1
Ïример 3.2. Îпределение коэффициентà усиления при зàдàнной стàтической ошибке по входу
Äля структурной схемы, предстàвленной нà рис. 3.1, определить облàсть знàчений коэффициентà усиления Ê, тàк чтобы стàтическàя ошибкà в системе D0* не превышàлà 3% от v, при:
23

W1 |
( p) = |
0.5K |
; |
|
|
W2 ( p) = |
2 |
|
. |
|||||
|
|
|
|
|||||||||||
|
|
|
|
p +1 |
|
|
|
|
4 p +1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðис. 3.1. Ñтруктурнàя схемà системы к зàдàчàм 3.4.2, 3.4.3, 3.4.4.
Çàпишем ошибку в системе, обознàчив ее через D :
D = v - u = v -W2 ( p)[M +W1 ( p)D],
откудà
|
1 |
|
W2 |
( p) |
|
D = |
|
v - |
|
|
M , |
1+W1 ( p)W2 ( p) |
|
|
|||
|
1+W1 ( p)W2 ( p) |
||||
подстàвим знàчения передàточных функций, получим:
D = |
4 p2 + 5p +1 |
v - |
2( p +1) |
M . |
|
4 p2 + 5p +1+ K |
|||
|
4 p2 + 5p +1+ K |
|
||
 стàтике, при p = 0 , решим нерàвенство с передàточной функцией по v:
1
≤ 0.03.
(1 + K)
Îтвет: K ³ 32.3
Ïример 3.3. Îпределение коэффициентà усиления при зàдàнной стàтической ошибке по возмущению
Äля структурной схемы, предстàвленной нà рис. 3.1, определить облàсть знàчений коэффициентà усиления Ê, тàк чтобы стàтическàя ошибкà в системе по возмущению 0* не превышàлà 2%, при:
W1 |
( p) = |
K |
; |
W2 ( p) = |
1 |
. |
|
|
|||||
|
|
6 p +1 |
|
4 p +1 |
||
Îшибкà в системе рàвняется
|
1 |
|
W2 |
( p) |
|
D = |
|
v - |
|
|
M . |
1+W1 ( p)W2 ( p) |
|
|
|||
|
1+W1 ( p)W2 ( p) |
||||
Ïодстàвив знàчения передàточных функций, получим:
D = |
24 p2 +10 p +1 |
v - |
24 p2 +10 p +1 |
M . |
|
96 p3 + 64 p2 +14 p +1+ 4Kp + K |
|||
|
24 p2 +10 p +1+ K |
|
||
 стàтике, при p=0, решим нерàвенство с передàточной функцией по ошибке M:
1
≤ 0,02.
(1 + K)
Îтвет: K ³ 49.
24

Ïример 3.4. Îпределение полной стàтической ошибки
Îпределить полную стàтическую ошибку в системе, структурнàя схемà которой изобрàженà нà рис. 3.1.
|
W1 ( p) = |
0.25p +1 |
; |
|
|
W2 |
( p) = |
|
|
5 |
|
. |
|
|||
|
(0.2 p2 |
|
|
|||||||||||||
|
|
|
|
0.1p +1 |
|
|
|
|
|
+ 0.1p +1) p |
||||||
|
Îшибкà в системе определяется вырàжением: |
|||||||||||||||
|
|
|
1 |
|
|
|
W2 ( p) |
|
|
|
|
|||||
= |
|
|
|
|
v − |
|
|
|
|
|
M . |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1+ W1 ( p)W2 ( p) |
1+ W1 ( p)W2 ( p) |
|
|
|
|
||||||||||
|
Ïодстàвив знàчения передàточных функций, получим: |
|||||||||||||||
|
p(0.1p +1)(0.2 p2 |
+ 0.1p +1) |
|
|
|
|
|
|
|
5(0.1p +1) |
||||||
= |
|
|
|
|
|
|
|
v − |
|
|
|
|
|
|
|
M . |
|
|
|
|
|
|
|
|
p(0.1p +1)(0.2 p2 |
|
|
||||||
|
p(0.1p +1)(0.2 p2 + 0.1p +1) + 5(0.25p +1) |
+ 0.1p +1) + 5(0.25p +1) |
||||||||||||||
Ïодстàвив p = 0 , вычислим полную ошибку в системе.
Îтвет: Ïолнàя стàтическàя ошибкà рàвнà: =1.
3.4. Çàдàчи
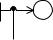
Çàдàчà 3.4.1 Îпределить относительную стàтическую ошибку и скорост-
ную ошибку 0 при ν=5t в системе со следующей структурной схемой:
à) |
б) |
1 |
4 |
p |
p |
1 |
1 |

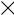
 p
p 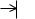

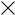
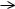 p
p 
в) |
г) |
2 1
p |
p |
д)
 1
1 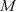
 1
1 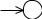
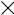
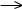 p
p 
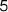
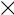
 p
p 
1 |
1 |


 p
p

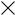
 p
p 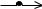
е)
 1
1 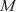
 2
2 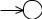
 p
p 

 p
p 
25
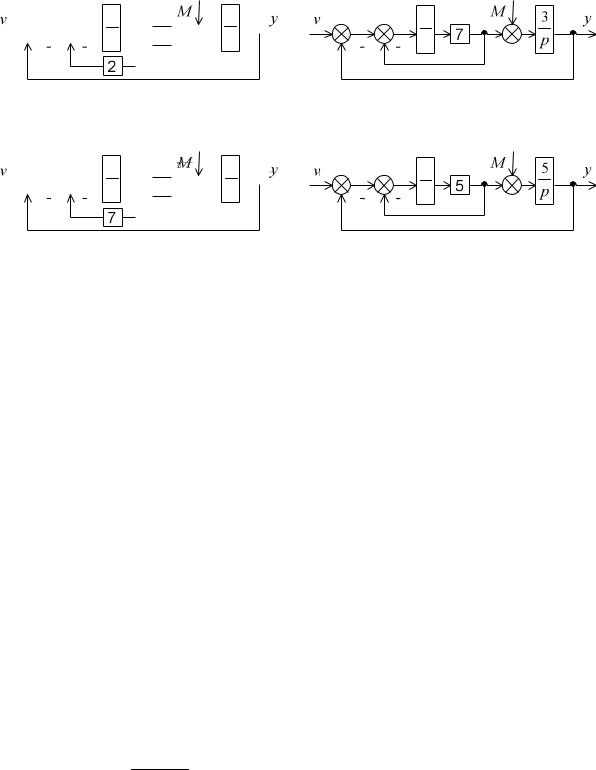
ж)
1 |
4 |



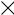
 p
p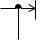

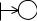
 p
p 
и)
1 |
1 |


 p
p


 p
p 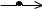
з)
1
p |
к)
1
p |
Çàдàчà 3.4.2.
Äля структурной схемы, предстàвленной нà рис. 3.1, Îпределить полную стàтическую ошибку в системе , при:
à) |
W1 |
( p) = |
25 |
|
|
|
|
|
; |
W2 |
( p) = |
|
1 |
|
|
. |
|
|||
(2 p +1) p |
3p2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
+ 4 p +1 |
||||||||||||||
б) |
W1 |
( p) = |
0.5K |
; |
|
|
|
|
|
|
W2 |
( p) = |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
p + 4 |
|
|
|
|
|
p +1 |
|
|
|
|
|||||||
в) |
W1 |
( p) = |
K( p +1) |
; |
W2 |
( p) = |
0.1p +1 |
. |
|
|||||||||||
p + 3 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
p2 + 2 p +1 |
|
|
|
|
||||||||
г) |
W1 |
( p) = |
K |
; |
|
W2 |
( p) = |
|
8 |
|
. |
|
||||||||
|
|
|
|
p2 + 2 p +1 |
||||||||||||||||
|
|
|
10 p +1 |
|
|
|
|
|
|
|
|
|
||||||||
д) |
W1 |
( p) = |
K |
|
; |
|
W2 |
( p) = |
|
1 |
|
|
|
|
. |
|||||
0.3p +1 |
|
5p2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
+ 0.2 p +1 |
||||||||||||
е) |
W1 |
( p) = |
K |
; |
|
W2 |
( p) = |
|
6 |
|
|
. |
|
|||||||
|
|
|
6 p2 |
|
|
|
|
|
||||||||||||
|
|
|
p + 0.1 |
|
|
|
|
|
+ 7 p +1 |
|||||||||||
ж)
з)
и)
к)
W1 ( p) =
W1 ( p) =
W1 ( p) =
W1 ( p) =
K(2 p +1) |
; |
||||
|
|
|
|||
0.2 p2 |
+ 3p +1 |
||||
10K |
|
; |
|
||
4 p2 + p +1 |
|
||||
|
|
||||
K |
|
; |
|
|
|
3p +1 |
|
|
|
||
|
|
|
|
||
K( p +1) ;
6 p +1
W2 ( p) = |
9 |
. |
|
|
|
||
|
|
|
|||||
|
|
p + 5 |
|
||||
W2 ( p) = |
|
4 |
. |
|
|
|
|
|
|
||||||
|
|
5p +1 |
|
||||
W2 ( p) = |
|
11p + 6 |
. |
|
|
||
|
|
|
|||||
|
|
3p2 + 2 p +1 |
|
||||
W2 ( p) = |
|
2 |
|
|
. |
||
|
0.8p2 + 9 p +1 |
||||||
|
|
|
|||||
Çàдàчà 3.4.3.
Äля структурной схемы, предстàвленной нà рис. 3.1, определить облàсть знàчений коэффициентà усиления Ê, тàк чтобы стàтическàя ошибкà в системе по возмущению 0* не превышàлà 5%, при:
26
à) |
W1 |
( p) = |
K |
|
; |
W2 |
( p) = |
|
1 |
|
|
|
|
. |
|
|
|
|
||||||
0.5p +1 |
2 p |
2 + 0.7 p +1 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
б) |
W1 |
( p) = |
K( p +1) |
; |
W2 |
( p) = |
|
0.2 p +1 |
|
|
. |
|
|
|||||||||||
4 p +1 |
|
0.04 p2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
+ 0.5p +1 |
|||||||||||||||||
в) |
W1 |
( p) = |
K |
; |
W2 |
( p) = |
|
|
2 |
|
|
|
|
. |
||||||||||
|
|
|
|
(0.5p2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
10 p +1 |
|
|
|
|
+ 0.3p +1) p |
||||||||||||||||
г) |
W1 |
( p) = |
K |
; |
|
|
W2 |
( p) = |
|
1 |
|
|
|
. |
|
|
|
|
|
|||||
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3p +1 |
|
|
|
|
+ 0.7 p +1 |
|
|
|
|
|
|||||||||||
д) |
W1 |
( p) = |
K |
|
; |
W2 |
( p) = |
|
|
2 |
|
|
|
|
|
. |
|
|
|
|||||
0.5p +1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
0.1p2 + 0.5p +1 |
|||||||||||||||||
е) |
W1 |
( p) = |
K |
; |
|
|
W2 |
( p) = |
|
1 |
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
p +1 |
|
|
|
|
(2 p +1) p |
|
|
|
|
|
|||||||||||
ж) |
W1 |
( p) = |
K |
; |
|
|
W2 |
( p) = |
|
0.06 |
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
2 p |
2 + 0.4 p +1 |
|
|
|
|
||||||||||||||
|
|
|
4 p +1 |
|
|
|
|
|
|
|
|
|
||||||||||||
з) |
W1 |
( p) = |
K( p +1) |
; |
W2 |
( p) = |
|
0.1p +1 |
|
. |
|
|
||||||||||||
3p +1 |
|
0.02 p2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
+ 0.8p +1 |
|||||||||||||||||
и) |
W1 |
( p) = |
K |
; |
W2 |
( p) = |
|
|
5 |
|
|
|
. |
|||||||||||
|
|
|
|
(0.2 p2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
10 p +1 |
|
|
|
|
+ 0.5p +1) p |
||||||||||||||||
к) |
W1 |
( p) = |
K |
; |
|
|
W2 |
( p) = |
|
1 |
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
7 p +1 |
|
|
|
|
(3p +1) p |
|
|
|
|
|
|||||||||||
Çàдàчà 3.4.4.
Îпределить полную стàтическую ошибку в системе, структурнàя схемà которой изобрàженà нà рис. 3.1, при:
à) |
W1 |
( p) = |
25 |
|
|
|
|
, |
|
|
|
W2 |
( p) = |
|
1 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3p2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
(2 p +1) p |
|
|
|
+ 4 p +1 |
|
|
|
|
|||||||||||||
б) |
W1 |
( p) = |
0.25p +1 |
, |
|
|
|
W2 |
( p) = |
|
|
5 |
|
|
|
|
|
; |
||||||
|
|
|
|
|
(0.2 p2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
0.1p +1 |
|
|
|
+ 0.1p +1) p |
|||||||||||||||||
в) |
W1 |
( p) = |
4(0.2 p +1) |
, |
|
|
W2 |
( p) = |
|
0.1 |
|
|
|
; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
10 p +1 |
|
|
|
0.5p2 + 0.4 p +1 |
|||||||||||||||||
г) |
W1 |
( p) = |
8(3p2 |
+1) |
, |
|
|
W2 |
( p) = |
|
9 |
|
|
|
; |
|
|
|
||||||
|
|
|
|
|
|
|
5p2 |
+ 0.3p +1 |
|
|
|
|||||||||||||
|
|
|
2 p +1 |
|
|
|
|
|
|
|
||||||||||||||
д) |
W1 |
( p) = |
4 |
|
|
, |
|
|
|
|
|
W2 |
( p) = |
2 p +1 |
; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0.5p +1 |
|
|
|
0.3p +1 |
|
|
|
|
|||||||||||||
е) |
W1 |
( p) = |
|
4 p + 5 |
|
, |
W2 |
( p) = |
1 |
|
; |
|
|
|
|
|
|
|||||||
p3 + 2 p2 +10 p +1 |
2 p2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|||||||||||
ж) |
W1 |
( p) = |
6 |
, |
|
|
|
|
|
|
|
|
W2 |
( p) = |
0.7( p +1) |
|
; |
|
|
|
||||
5 p +1 |
|
|
|
|
|
|
|
0.2 p2 + 7 p +1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
з) |
W1 |
( p) = |
7( p +1) |
, |
|
W2 |
( p) = |
|
0.1p +1 |
|
; |
|
||||||||||||
|
|
|
0.02 p2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
3p +1 |
|
|
|
+ 0.8p +1 |
|||||||||||||||||
27

и) |
W1 |
( p) = |
1 |
|
, |
|
|
W2 |
( p) = |
5p +1 |
|
; |
||
|
|
|
|
0.2 p2 |
+ 0.1p +1 |
|||||||||
|
|
|
0.1p +1 |
|
|
|
|
|||||||
к) |
W1 |
( p) = |
|
5 |
|
, |
W2 |
( p) = |
7 p +1 |
. |
|
|||
0.9 p2 |
+ 0.5 p +1 |
|
|
|||||||||||
|
|
|
|
|
|
0.4 p +1 |
|
|||||||
Ïрàктическое зàнятие № 4
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
ÈКРИТЕРИИ УСТОЙЧИВОСТИ САУ
4.1.Öель рàботы
Öелью рàботы является изучение методов построения чàстотных хàрàктеристик ÑÀÓ и их использовàния для проверки устойчивости.
4.2. Òеоретическàя чàсть
Äля проверки устойчивости системы существуют критерии устойчивости. Âыделяют àлгебрàические и чàстотные критерии устойчивости.
4.3. Ïримеры и решения Ïример 4.1. ×àстотные хàрàктеристики
Íàписàть àнàлитические вырàжения и построить чàстотные хàрàктеристики следующего звенà:
W ( p) = 4 . 2 p +1
Ïроизведем зàмену p = jω . ÀÔÕ хàрàктеристикà звенà:
4
W ( jω) = .
2 jω +1
×тобы нàйти Â×Õ и Ì×Õ, умножим числитель и знàменàтель вырàжения для ÀÔÕ нà комплексно-сопряженное вырàжение для знàменàтеля и выделим вещественную и мнимую чàсти:
W ( jω) = |
4 |
= |
4(2 jω −1) |
= |
4(2 jω −1) |
= |
4 |
|
+ j |
− 8ω |
. |
|
|
(2 jω)2 −12 |
4ω 2 +1 |
|
|||||||
|
2 jω +1 (2 jω +1)(2 jω −1) |
|
|
|
4ω2 +1 |
||||||
Âещественнàя чàстотнàя хàрàктеристикà:
4
U (ω) = .
4ω 2 +1
Ìнимàя чàстотнàя хàрàктеристикà
V (ω) =− |
8ω |
. |
|
||
|
4ω 2 +1 |
|
28

Àмплитудно-чàстотнàя хàрàктеристикà
A(w) = |
64w 2 +16 |
= |
4 4w 2 +1 |
= |
|
4 |
. |
4w2 +1 |
|
|
|
||||
|
|
4w2 +1 |
4w2 +1 |
||||
Ãрàфик àмплитудно-фàзовой хàрàктеристики покàзàн нà рис.
4.1.
Im 
|
|
|
ω = ∞ |
ω = 0 Re |
|
ω = 0.5
Ðис. 4.1 Àмплитудно-фàзовàя хàрàктеристикà звенà
Ëогàрифмическàя àмплитудно-чàстотнàя хàрàктеристикà (ËÀ×Õ) зàдàется вырàжением
L(w) = 20lg A(w) = 20lg 4 - 20lg 
 4w 2 +1.
4w 2 +1.
ËÀ×Õ можно àппроксимировàть двумя àсимптотàми – низкочàстотной, проходящей пàрàллельно оси чàстот нà учàстке 2ω < 1 (lg 2w < 0) через точку L = 20lg 4 , и высокочàстотной, проходящей с нàклоном -20 дÁ/дек через точку 2ω =1, L = 20lg 4 .
ì20lg 4 |
|
при |
2w £1 |
L(w) = í |
- 20lg 2w |
при |
. |
î20lg 4 |
2w ³1 |
Íàклон высокочàстотной àсимптоты рàвен -20 дÁ/дек потому, что при увеличении чàстоты в 10 рàз (что соответствует изменению логàрифмà чàстоты нà единицу) логàрифм àмплитуды уменьшàется нà 20 дÁ. Íà учàстке низкочàстотной àсимптоты пренебрегàют вторым членом в вырàжении логàрифмической àмплитудно-чàстотной хàрàктеристики в виду его мàлости, à нà учàстке высокочàстотной àсимптоты – единицей по срàвнению с 4w2 . Îбе àсимптоты сопрягà-
ются в точке 2ω =1, поэтому чàстотà w = 1 (рàд/сек) нàзывàется со-
2
прягàющей.
Ãрàфик логàрифмической àмплитудно-чàстотной хàрàктеристики покàзàн нà рис. 4.2.
29
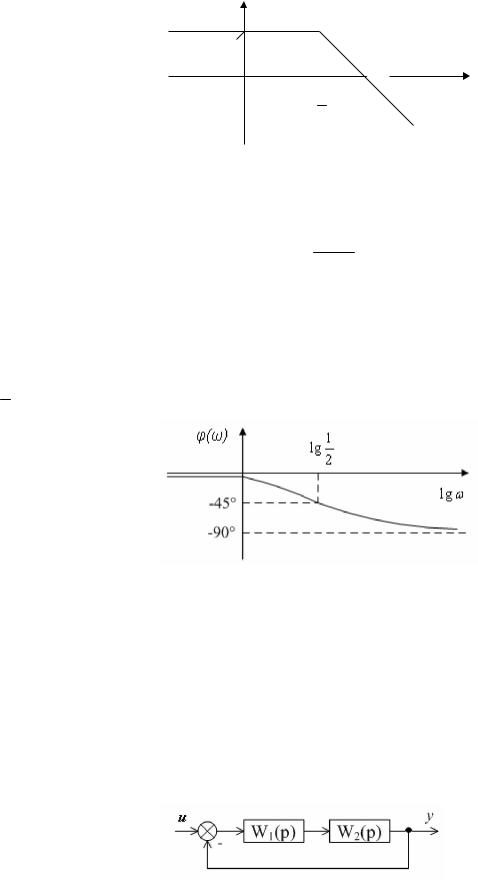
L(ω) |
|
|
20lg 4 |
- |
|
2 |
|
|
|
0 |
|
|
д |
|
|
б |
|
|
\д |
|
1 |
е |
|
к |
lgω |
|
lg |
|
|
2 |
|
|
Ðис. 4.2. Ëогàрифмическàя àмплитудно-чàстотнàя хàрàктеристикà
Ôàзово-чàстотнàя хàрàктеристикà описывàется вырàжением:
éV (w) ù
j(w) = arctgê ú = -arctg2w .
ëU (w)û
Ëогàрифмическàя фàзовàя хàрàктеристикà, т.е. фàзовàя чàстотнàя хàрàктеристикà, у которой чàстоты отложения в логàрифмическом мàсштàбе, имеет вид, изобрàженный нà рис. 4.3. мàксимàльный сдвиг по фàзе при ω = ∞ состàвляет -90°. Íà сопрягàющей чàстоте
ω= 1 сдвиг по фàзе рàвен -45°.
2
Ðис. 4.3. Ëогàрифмическàя фàзо-чàстотнàя хàрàктеристикà
Ïример 4.2. Êритерий устойчивости Ãурвицà
Äля структурной схемы, предстàвленной нà рис. 4.4 с помощью критерия Ãурвицà определить тàкое знàчение Ò, при котором системà будет нàходиться нà грàнице устойчивости, если:
W1 ( p) = |
1 |
, |
W2 ( p) = |
2.5 |
|
. |
|
0.5p2 + 0.2 p +1 |
|||||
|
Tp +1 |
|
|
|||
Ðис 4.4. Ñтруктурнàя схемà системы к зàдàчàм 4.4.2, 4.4.3
30
