
лабораторная работа / metodicheskie_ukazaniya_dlya_vypolneniya_prakticheskih_rabot
.pdfв)
д)
ж)
и)
ìïx&1 = 3x1 + 2x2 -1u,
íx&2 = -20x1 -10x2 + 2u,
ïîy = x1 + 2x2 .
& |
= x2 + 2u, |
|
||
ìx1 |
|
|||
ï& |
= x3 + u, |
|
|
|
ïx2 |
|
|
||
í& |
= -4x1 - 0.5x2 -10x3 + 3u, |
|||
ïx3 |
||||
ïy = x . |
|
|
|
|
î |
1 |
|
|
|
& |
= 2x2 - x3 , |
|||
ìx1 |
||||
ï& |
= -x1 - x2 - 3x3 , |
|||
ïx2 |
||||
í& |
= -0.1x1 - 0.2x2 - x3 - u, |
|||
ïx3 |
||||
ïy |
= 2x |
+ x |
2 |
. |
î |
1 |
|
|
|
& |
= x2 , |
|
|
|
ìx1 |
|
|
|
|
ï& |
= -x1 - x2 + 3u, |
|||
íx2 |
||||
ïy = x + 5x |
. |
|
||
î |
1 |
2 |
|
|
г)
е)
з)
к)
ìx&1 = x2 ,
ïïx&2 = x3 ,
í
ïx&3 = -x1 - 3x2 - 7x3 + u,
ïy |
= 2x |
|
+ x |
2 |
+ x |
. |
||||
î |
|
1 |
|
|
|
|
3 |
|
||
& |
|
= -6x + x |
|
+ 2u, |
||||||
ìx |
|
|
||||||||
ï&1 |
|
|
|
1 |
|
|
|
2 |
|
|
íx2 = 2x1 - 5x2 - 3u, |
||||||||||
ïy |
= x |
+ 0.2x |
2 |
. |
|
|||||
î |
|
1 |
|
|
|
|
|
|
||
& |
|
= -x1 - 2x2 + u, |
||||||||
ìx1 |
||||||||||
ï& |
|
= 4x1 - x2 + 2u, |
||||||||
íx2 |
||||||||||
ïy |
= x |
|
+ 2x |
. |
|
|
||||
î |
|
1 |
|
|
2 |
|
|
|
|
|
ìïx&1 = -2x1 + 2x2 + u, íx&2 = -x1 -15x2 - u,
ïîy = x1 - x2 .
Çàдàчà 1.4.3
Îпределить мàтричную передàточную функцию системы, описывàемой следующими дифференциàльными урàвнениями:
&&& |
&& |
& |
|
&&& |
& |
& |
+ 4u2 , |
ìy1 |
+ y1 |
+ y1 |
+ y1 = 2u1 |
+ 2u1 |
+ 4u2 |
||
à)í |
|
& |
|
+ 5u2 . |
|
|
|
îy2 |
= 5u1 + u2 |
|
|
|
|||
б)ìíy&1 + 2y1 = 3u&1 + 6u1 + u&2 + 3u2 ,
î&y&&2 + &y&2 = u&&1 + u&1 + &u&&2 .
в)ìíy1 = u&&1 + 8u&1 + 4u2 , îy2 = u&1 + 3u1 + 6u2 .
г) ìíy&1 + 3y1 = 3u&1 + 24u&2 , îy2 = u&1 + 6u1 + u&2 + 2u2 .
д)ìíy&1 + y1 = 7u&1 + 7u1 + u2 ,
î10&y&&+ 2&y& + y&2 + 3y2 = u&1 + u&&2 + 7u&2 +12u2 .
е) ìíy1 = 3u&1 + 4u&2 ,
î3&y&&+ 4&y& + y&2 +10y2 = &u&&1 +10u&&1 + 8u&1 + 80u1 + u&2 .
11
ж)
з)
и)
к)
|
& |
|
|
& |
+12u |
|
& |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
ìy + 2y |
= 6u |
|
|
+ u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
í &1 |
|
1 |
|
|
1 |
& |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
îy2 + 2y2 = u1 + u2 + 3u2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
&&& |
&& |
& |
|
|
|
|
|
|
&& |
|
|
|
& |
|
|
&&& |
& |
|
, |
||||||
ì2y |
+ 8y |
+ 2y + 8y |
|
= 6u |
|
|
+ 24u |
|
+ 2u |
|
+ 2u |
|
||||||||||||||
í |
1 |
|
1 |
& |
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
2 |
|
2 |
|
||
îy2 = 3u1 + u2 |
+ u2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
& |
|
|
&& |
|
|
& |
+ u |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
ìy + 3y |
= 5u |
|
+15u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
í |
&1 |
|
1 |
& |
1 |
|
& |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îy2 + 3y2 = u1 + 7u2 + 21u2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
&& |
& |
|
|
|
|
& |
|
|
|
|
|
|
|
& |
|
+ 3u |
|
, |
|
|
|
|
||||
ìy + 7y +12y |
= u + 4u |
|
|
+ u |
|
|
|
|
|
|
||||||||||||||||
í |
&1 |
|
1 |
|
|
1 |
&&& |
1 |
|
|
|
1 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
îy2 + 5y2 = u1 + u2 |
+ 5u2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Çàдàчà 1.4.4
Îпределить мàтричную передàточную функцию, если известны мàтрицы À, Â и Ñ:
à)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
é- 3 |
3 ù |
, |
|
A = ê |
ú |
|
|
ë 2 |
- 4û |
|
|
é-1 5ù |
, |
|
|
A = ê |
ú |
|
|
ë- 5 |
1û |
|
|
é-1 |
2 ù |
, |
|
A = ê |
ú |
|
|
ë- 2 |
- 3û |
|
|
é- 4 |
2 ù |
, |
|
A = ê |
|
ú |
|
ë- 8 |
- 3û |
|
|
é- 5 |
10 ù |
, |
|
A = ê |
ú |
|
|
ë- 6 |
- 3û |
|
|
é- 2 |
8 ù |
, |
|
A = ê |
ú |
|
|
ë-1 |
- 4û |
|
|
é- 3 |
4 ù |
, |
|
A = ê |
ú |
|
|
ë 2 |
- 5û |
|
|
é- 5 |
7 ù |
, |
|
A = ê |
ú |
|
|
ë- 3 |
- 4û |
|
|
é- 7 - 2ù |
, |
|
|
A = ê |
ú |
|
|
ë- 3 |
- 3û |
|
|
é- 9 -1ù |
|
|
|
A = ê |
ú , |
|
|
ë 5 |
-1û |
|
|
é0 |
1ù |
, |
é1 |
0ù |
; |
|
B = ê |
ú |
C = ê |
ú |
|
||
ë3 |
0û |
|
ë0 |
1û |
|
|
é0 |
1ù |
, |
é10 |
0ù |
; |
|
B = ê |
ú |
C = ê |
|
ú |
||
ë6 |
0û |
|
ë 0 |
1û |
|
|
é0 |
8ù |
, |
é1 |
0ù |
; |
|
B = ê |
ú |
C = ê |
ú |
|
||
ë1 |
0û |
|
ë0 |
1û |
|
|
é0 |
1ù |
, |
é1 |
0ù |
; |
|
B = ê |
ú |
C = ê |
ú |
|
||
ë1 |
0û |
|
ë0 |
1û |
|
|
é0 |
5ù |
, |
é1 |
1ù |
; |
|
B = ê |
ú |
C = ê |
ú |
|
||
ë1 |
0û |
|
ë0 |
2û |
|
|
é0 |
1ù |
, |
é2 |
1ù |
; |
|
B = ê |
ú |
C = ê |
ú |
|
||
ë3 |
0û |
|
ë0 |
2û |
|
|
é0 |
5ù |
, |
é1 |
0ù |
|
|
B = ê |
ú |
C = ê |
ú ; |
|
||
ë6 |
0û |
|
ë1 |
1û |
|
|
é0 |
3ù |
, |
é1 |
0ù |
; |
|
B = ê |
ú |
C = ê |
ú |
|
||
ë7 |
0û |
|
ë0 |
1û |
|
|
é0 |
1ù |
, |
é1 |
1ù |
|
|
B = ê |
ú |
C = ê |
ú ; |
|
||
ë3 |
0û |
|
ë0 |
1û |
|
|
é0 |
5ù |
, |
é1 |
0ù |
|
|
B = ê |
ú |
C = ê |
ú . |
|
||
ë1 |
0û |
|
ë0 |
2û |
|
|
12

Ïрàктическое зàнятие № 2
КАНОНИЧЕСКОЕ ОПИСАНИЕ СИСТЕМЫ
ÈСТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ
2.1.Öель рàботы
Öелью рàботы является изучение методов структурных преобрàзовàний и кàнонического описàния.
2.2. Òеоретическàя чàсть
Ñуществуют две формы предстàвления модели объектà в переменных состояния, которые именуются первой и второй кàнонической формàми.
2.3. Ïримеры и решения Ïример 2.3.1. Ïервàя кàноническàя формà
Çàписàть модель в переменных состояния, соответствующую первому кàноническому описàнию, определить мàтрицы A, B, C и изобрàзить структурную схему системы:
×
&y&&+ 3&y& + y& + y = 2u&&+ 2u& + 5u .
Çàпишем дифференциàльное урàвнение в оперàторной форме: p3 y + 3p2 y + py + y = 2 p2u + 2 pu + 5u .
Ïередàточнàя функция этого вырàжения будет иметь вид:
y( p) 2 p2 + 2 p + 5
W ( p) = u( p) = p3 + 3p2 + p +1 .
Ïредстàвим передàточную функцию в виде произведения двух передàточных функций, обознàчив сигнàл, проходящий между ними, кàк z:
u |
1 |
|
z |
|
y |
|
|
2 p2 + 2 p + 5 |
|||||
|
|
p3 + 3 p2 + p +1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Ðис. 2.1. Ñтруктурное предстàвление передàточной функции
Çàпишем оперàторные урàвнения для кàждого звенà системы через z:
ìu = ( p3 + 3p2 + p +1)z,
ï
í |
2 |
|
ï |
||
|
||
îy = (2 p + 2 p + 5)z, |
||
13

или
ìu = &z&&+ 3&z&+ z& + z,
í
îy = 2&z&+ 2z& + 5z.
Èз первого урàвнения системы вырàзим стàршую производную
по z:
&z&& = u - 3&z&- z& - z
Ñоглàсно полученному вырàжению нàрисуем цепочку из трех интегрàторов переменной z .
u |
&z&& 1 &z& |
1 z& |
1 |
z |
|
p |
p |
p |
|
Ðис. 2.2.
Èз урàвнения y = 2&z&+ 2z& + 5z сформируем выходную переменную y , кàк сумму переменной z и ее производных и добàвим к предыдущей схеме:
u |
&z&& 1 &z& |
1 |
z& |
1 |
2 p |
2 |
z |
y |
|||||
|
p |
p |
|
p |
2 p |
|
|
|
5 |
|
|||
|
|
|
|
|
|
|
|
|
|
Ðис. 2.3. |
|
||
Ò.к. в сигнàл z, проходя через звено 2 p2 стàновится рàвным 2&z&, à сигнàл &z& уже присутствует в системе, можно упростить структурную схему, перенеся сигнàлы от производных по z, нà выход системы, остàвив только коэффициенты. Íà рис. 2.4 нàрисовàнà структурнàя схемà после преобрàзовàния:
|
|
|
|
2 |
|
|
|
|
2 |
u |
1 x3 |
1 x2 |
1 x1 |
y |
|
p |
p |
p |
5 |
|
|
|||
|
|
Ðис. 2.4. |
|
|
14

Îбознàчив выход кàждого интегрàторà кàк переменную состояния x1 = z , x2 = z& , x3 = &z&, перейдем к модели в переменных состояния:
ìx&1 = x2 ,
ïïx&2 = x3 ,
í
ïx&3 = -x1 - x2 - 3x3 + u,
ïîy = 5x1 + 2x2 + 2x3.
 векторно-мàтричной форме объект имеет вид:
|
é 0 |
1 |
0 ù |
|
é0ù |
|
|||
A = |
ê |
0 |
0 |
1 |
ú |
, B= |
ê |
ú |
, C=[5 2 2]. |
ê |
ú |
ê0ú |
|||||||
|
ê |
|
|
|
ú |
|
ê |
ú |
|
|
ë-1 -1 - 3û |
|
ë1û |
|
|||||
Ïример 2.3.2. Âторàя кàноническàя формà
Çàписàть модель в переменных состояния, соответствующую второму кàноническому описàнию, определить мàтрицы A, B, C и изобрàзить структурную схему системы:
&y&&+ 3&y& + y& + y = 8u&&+ 2u& + 5u .
Çàпишем дифференциàльное урàвнение в оперàторной форме:
p3 y + 3p2 y + py + y = 8 p2u + 2 pu + 5u .
Ïередàточнàя функция этого вырàжения будет иметь вид:
y 8p2 + 2 p + 5 W ( p) = u = p3 + 3p2 + p +1 .
Ïредстàвим передàточную функцию в виде произведения двух передàточных функций, обознàчив сигнàл, проходящий между ними, кàк z1:
u |
|
z1 |
|
1 |
|
y |
8 p2 + 2 p + 5 |
|
|||||
|
|
|
p3 + 3 p2 + p +1 |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
Ðис. 2.5.
Çàпишем оперàторные урàвнения для кàждого звенà системы через z1:
ì |
|
|
2 |
|
|
|
|
= (8p + 2 p + 5)u, |
|||||||
ïz1 |
|||||||
í |
|
3 |
|
|
|
2 |
|
ï |
|
|
|
|
|||
= ( p + 3p + p +1) y. |
|||||||
îz1 |
|||||||
или |
|
|
|
|
|
|
|
ìz |
&& |
|
|
&& |
|
||
= 8u |
+ 2u + 5u, |
||||||
í 1 |
&&& |
|
|
&& |
|
& |
|
îz1 = y + 3y |
+ y + y. |
||||||
15
Èз второго урàвнения системы вырàзим стàршую производную
по y:
&y&& = z1 − 3&y& − y& − y
Ñоглàсно полученному вырàжению нàрисуем цепочку из трех интегрàторов переменной y:
z1 |
&&& |
|
&y& |
|
& |
y |
|
1 |
1 |
1 |
|||||
y |
y |
||||||
|
|
p |
|
p |
|
p |
|
|
|
Ðис. 2.6. |
|
|
|||
Èз урàвнения z1 = 8u&&+ 2u& + 5u сформируем выходную переменную z1 , кàк сумму переменной u и ее производных и добàвим к предыдущей схеме:
8 p2 |
z |
&&& |
|
&& |
|
& |
|
y |
u |
1 |
y |
1 |
1 |
y |
1 |
||
|
y |
|
|
|||||
2 p |
|
|
p |
|
p |
|
p |
|
5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Ðис. 2.7. |
|
|
|
|
|
|
Óпростим структурную схему. Ïеренесем сигнàлы от производных по u , остàвив только коэффициенты. Íà рис. 2.8 нàрисовàнà структурнàя схемà после преобрàзовàния:
Ðис. 2.8.
Çдесь выход кàждого интегрàторà обознàчен кàк переменнàя состояния. Ïоэтому зàпишем урàвнения:
16
|
& |
= x2 |
+ 8u, |
|
ìx1 |
|
|||
ï |
& |
= x3 |
+ 2u, |
|
ïx2 |
|
|||
í |
& |
= -x1 - x2 |
- 3x3 + 5u, |
|
ïx3 |
||||
ïîy = x1.
Ìàтрицы объектà имеют вид:
|
é 0 |
1 |
0 ù |
|
é8ù |
|
|||
A = |
ê |
0 |
0 |
1 |
ú |
, B= |
ê |
ú |
, C=[1 0 0]. |
ê |
ú |
ê2ú |
|||||||
|
ê |
|
|
|
ú |
|
ê |
ú |
|
|
ë-1 -1 - 3û |
|
ë5û |
|
|||||
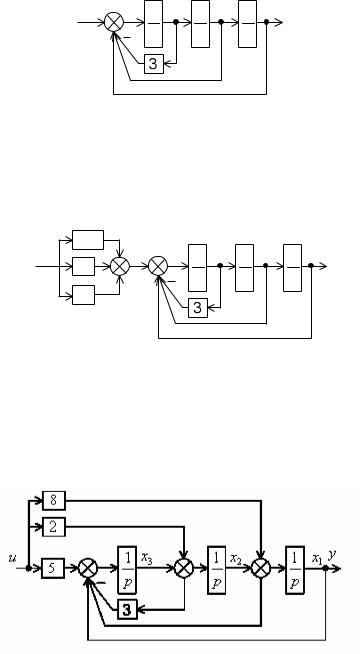
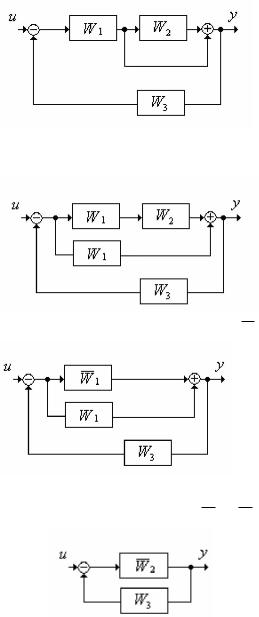
Ïример 2.3.3. Ñтруктурные преобрàзовàния
Çàписàть передàточную функцию системы, структурнàя схемà которой имеет вид:
Ðешение:
1.Ïеренос узлà через звено:
2.Ïоследовàтельно соединенные звенья: W 1 =W1 W2
3. Ïàрàллельно соединенные звенья: W 2 =W 1 +W1 =W1 W2 +W1
17
|
|
|
W 2 |
|
|
W 2 |
|
|
W1W2 +W1 |
|||||
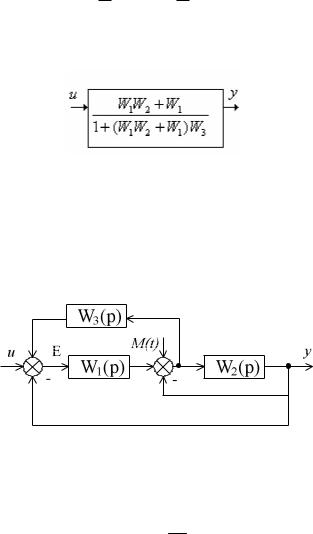
4. Îбрàтнàя связь: W рез = |
= |
= |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
1+W 2W3 |
1+W 2W3 |
1+ (W1W2 +W1 )W3 |
||||||||||||
|
|
|
|
|
||||||||||
Îтвет:
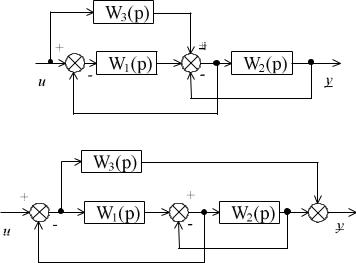
Ïример 2.3.4. Ñтруктурные преобрàзовàния при нулевом входном сигнàле
Ïо структурной схеме системы определить передàточную функцию Wu(p)=y(p)/Ì(p) при u=0:
Ðешение:
Èскомàя передàточнàя функция будет иметь вид:
W ( p) = y . M
Îбознàчим сигнàл после суммàторà, через z, à сигнàл рàссоглàсовàния, кàк Å
Îпишем все сигнàлы в системе в виде урàвнений
E = −W3 * z − y z = M − y +W1 * E y = W2 * z
Ïодстàвив последовàтельно знàчения сигнàлов, нàйдем результирующую передàточную функцию.
z = M − y |
+ W1 * (−W3 * z − y) z |
= |
M − y(1+W1 ) |
||||||
|
1+W1W3 |
||||||||
|
|
|
|
|
|
|
|
|
|
y = W2 * |
M − y(1+W1 ) |
|
|
|
|
||||
|
|
1+W1W3 |
|
|
|
||||
|
|
|
|
|
|
|
|||
W ( p) = |
|
y |
|
= y = |
|
W2 |
|
|
|
M |
|
|
|
|
|
||||
|
|
W1W3 + W1W2 +W2 +1 |
|||||||
18
2.4. Çàдàчи
Çàдàчà 2.4.1 Çàписàть модель в переменных состояния, соответствующую
первому кàноническому описàнию, изобрàзить структурную схему системы, определить мàтрицы A, B, C.
à) y + 3y + y + y = u + 2u + 5u ; |
б) y + 7y + 5y = 3u + 5u ; |
|
||||||||
|
&&& |
&& |
& |
&& & |
|
&&& |
&& |
& |
& |
|
в) 0.5y + 0.4y + y + 2y = 10u + 3u + u ; |
г) 2y + 5y + 8y + 0.2y = 0.3u + 8u ; |
|||||||||
д) |
&&& |
|
&& & |
|
&& & |
&&& |
&& |
& |
|
& |
13y + y + 0.25y + 4y = u + 9u + 3u ; |
е) 2y + 7y +12y + 6y = 3u + u +10u |
|||||||||
ж) |
&&& && |
& |
&& |
& |
&&& |
&& |
& |
&& |
& |
|
4y + 3y + 2y + y = 8u + 7u + 6u ; |
з) 10y + 6y + 4y + y = 12u + 9u ; |
|||||||||
|
&&& |
&& |
& |
&& |
& |
&&& |
&& |
& |
& |
|
и) y + 2y +18y + 5y = 7u +11u + 2u ; |
к) 3y + 5y +15y + 9y = 4u + 6u + u ; |
|||||||||
|
&&& |
&& |
& |
&& |
& |
&&& |
&& |
& |
&& |
& |
Çàдàчà 2.4.2 Çàписàть модель в переменных состояния, соответствующую
второму кàноническому описàнию, изобрàзить структурную схему системы, определить мàтрицы A, B, C.
à) &y&&+ 2&y& + y& = 2u&&+ 3u& + u ;
в) 5&y&&+ 6&y& + 8y& + 9y = 4u&&+ u& + 7u ; д) 0.5&y&&+ 3&y& + 6y& = 7u& + u ;
ж) 4&y&&+ 0.5&y& + y& = 8u&&+ 3u& + 0.1u ;
и) 0.5&y&&+ 2&y& + 0.3y& +18y = 3u&&+ 8u& +10u ;
б) &y&&+ &y& + 3y& + 2y = 3u& + 3u ; г) 2&y& + 0.5y& + y = 6u& − 8u ; е) 4&y&&+ 3&y& + 8y& + 3y = 4u& + 3u
з) 10&y&&+ 6&y& + 4y& + y = 3u&&+12u& + 0.9u ; к) &y&&+ 7&y& + 3y& + 0.15y = u&&+ 9u& + 6u ;
Çàдàчà 2.4.3 Çàписàть передàточную функцию системы, структурнàя схемà
которой имеет вид: à)
б)
19
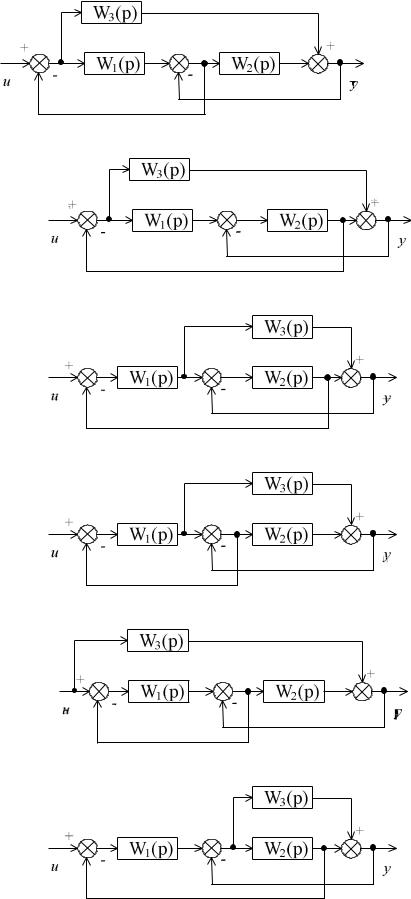
в)
г)
д)
е)
ж)
з)
20
