2.3. Основные законы распределения

Для использования на практике вероятностного подхода к оценке погрешностей результатов измерений прежде всего необходимо установить для данной погрешности вид аналитической модели закона распределения.

В метрологии встречаются разнообразные распределения. Результаты исследований 219 фактических распределений, имеющих место при измерении электрических и неэлектрических величин разнообразными приборами показали, что примерно 50% распределений принадлежат к классу экспоненциальных, 30% являются уплощенными, а остальные 20% - различными видами двухмодальных распределений.

Множество законов распределения СВ, используемых в метрологии, целесообразно классифицировать следующим образом:

- трапецеидальные (плосковершинные) распределения;

- уплощенные (приблизительно плосковершинные) распределения;

- экспоненциальные распределения;

- семейство распределений Стьюдента;

- двухмодальные распределения.

2.3.1. Трапецеидальные распределения

К трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Это симметричные распределения, у которых центр равен его математическому ожиданию .

Равномерное распределение (рис.2.5,а) описывается функцией распределения плотности вероятности

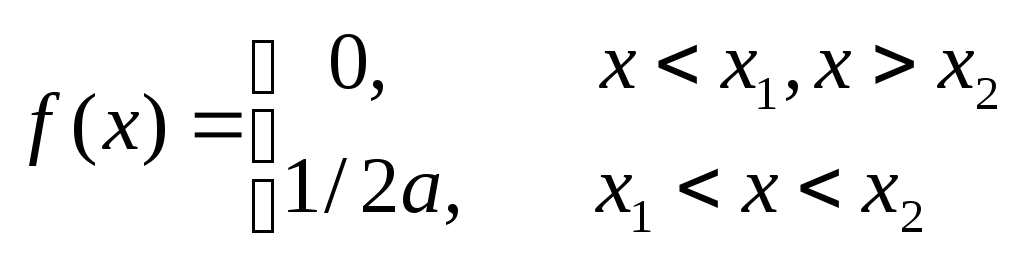(2.16)

Трапецеидальное распределение (рис. 2.5,б) образуется как композиция двух равномерных распределений с различным значением параметра . Ее функция распределения плотности вероятности имеет вид

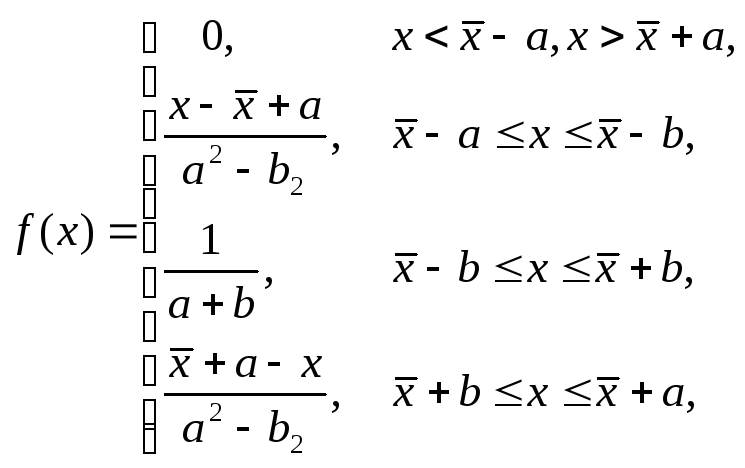(2.17)

Для центрированного распределения (рис.2.5,с) (находится в начале координат) и выражения принимают вид

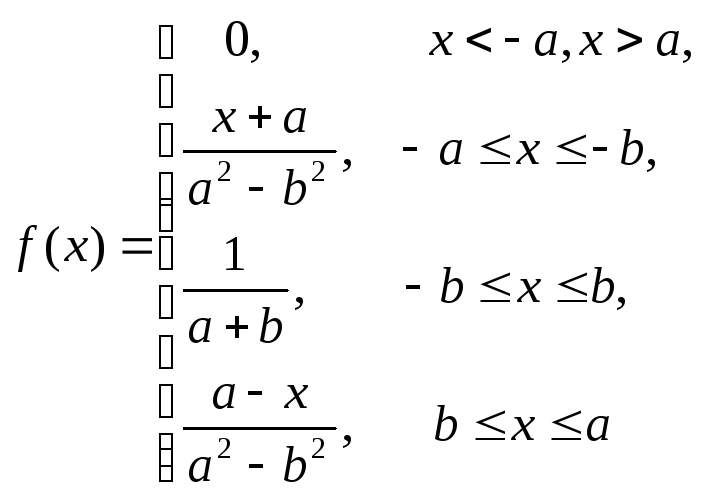(2.18)

Треугольное (Симпсона) распределение (рис.2.5,ж) – это частный случай трапецеидального , для которого размеры исходных равномерных распределений, из которых он образован одинаковы. Функция плотности вероятности для этого распределения имеет вид

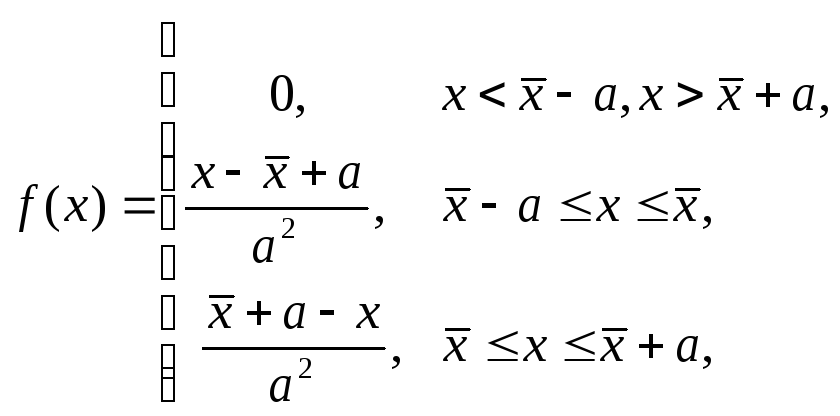(2.19)

Для центрированного распределения (рис.2.5,з)

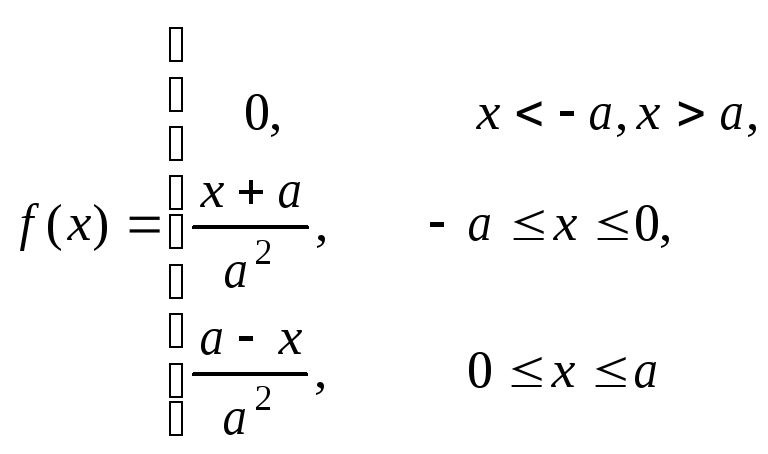(2.20)

Или эти выражения можно записать по другому

(2.21)

В вышеприведенных уравнениях – параметры распределения.

Математическое ожидание всех трапецеидальных распределений

Медианы, так как распределения симметричны, равны математическому ожиданию. У равномерного и трапецеидального распределений моды нет, а у треугольного она равна .

СКО в зависимости от распределения определяется по формуле

- равномерное ;

-трапецеидальное ;

- треугольное .

Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до a (равномерное).

Числовые параметры трапецеидальных распределений при различных отношениях ширины а и b 2-х исходных равномерных распределений приведены в таблице 2.1.

Таблица 2.1.