2. Геометрический смысл производной

Пусть функция определена и непрерывна на интервале (a, b). Пусть, далее, точка M на графике функции соответствует некоторому значению аргумента , а точка P – значению , где 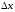- приращение аргумента. Проведём через точки M и P прямую и назовём её секущей. Обозначим через угол между секущей и осью Ox (рис. 56). Очевидно, что этот угол зависит от . Касательной S к графику функции в точке M будем называть предельное положение секущей MP при неограниченном приближении точки P по графику в точке M (или, что тоже самое, при ). Из рис. 56 следует, что

.

Так как при секущая MP переходит в касательную, то

где - угол, который образует касательная с осью Ox. С другой стороны,

3. Физический смысл производной

Предположим, что функция описывает закон движения материальной точки M по прямой линии, т.е. - путь, пройдённый точкой от начала движения за время t.

Тогда за время пройден путь , а за время - путь За промежуток времени точка M пройдёт отрезок пути (рис. 57). Отношение называется средней скоростью движения за время , а предел отношения при определяет мгновенную скорость точки в момент времени

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Теорема 4. Если функции u = u(х) и υ = υ(x) имеют производные в точке x₀, то сумма, разность, произведение и частное этих функций (частное при условии, что υ (x)≠0) также имеют производные в точке x₀ и справедливы следующие формулы:

(u±υ)´=u´±υ´; (u·υ)´=u´υ+uυ´;

ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ

I. = 0.

II = αх^{α – 1}(α – любое число), в частности

III. e, в частности .

IV. , в частности = е^х.

V. . VII. . IX. . XI. .

VI. . VIII. . X. . XII. .

ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Теорема 5. Если функция х = φ(t) имеет производную в точке t, а функция y = f(x) имеет производную в точке х = φ(t), то сложная функция f[φ(t)] имеет производную в точке t и имеет место следующая формула:

y′ (t) = f′(x) φ′(t). (1)

ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ

В теореме 2.7. рассматривалась сложная функция, где y зависела от t  через промежуточную переменную х. Возможна и более сложная зависимость – с двумя, тремя и большим числом промежуточных переменных, но правило дифференцирования остается прежним.

Так, например, если y = f(x), где x = φ(u), а u = ψ(v) и v = χ(t), то производную y′(t) следует искать по формуле

y′(t) = y′(x) x′(u) u′(v) v′(t). (2)

ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ И ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Пример. Используя правила и формулы дифференцирования, найти производную функции

f(x) = 5+ arcsin x + 3 arccos x + arctg x – 3 arcctg x.

Решение. Имеем

f′(x) = (5 + arcsin x + 3 arccos x + arctg x – 3 arcctg x)′ = (5)′ + (arcsin x)′ + 3 (arccos x)′ + (arctg x)′ – 3 (arcctg x)′ = 5ln5 + – + + = 5ln5 – + .

ПОНЯТИЕ ПРОИЗВОДНОЙ N-ГО ПОРЯДКА

Как уже отмечалось в п.1, производная функции сама является некоторой функцией аргумента x. Следовательно, по отношению к ней снова можно ставить вопрос о существовании и нахождении производной.

Назовем производной первого порядка.

Производная от производной некоторой функции называется производной второго порядка (или второй производной). Производная от второй производной называется производной третьего порядка (или третьей производной) и т.д. Производные, начиная со второй, называются производными высшего порядка и обозначаются так:

или

Производная n-го порядка есть производная от производной -го порядка, т.е.

Производные высших порядков имеют широкое применение в физике. Здесь мы ограничимся физическим толкованием второй производной . Если функция описывает закон движения материальной точки по прямой линии, то, как известно, первая производная есть мгновенная скорость точки в момент времени х, а вторая производная в таком случае равна скорости изменения скорости, т.е. ускорению движущейся точки в момент времени х.

ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ.

Будем говорить, что функция f(x) не убывает (не возрастает) на множестве Х, если для любых x₁ и x₂, принадлежащих Х, удовлетворяющих условию x₁ < x₂ , справедливо неравенство f(x₁) ≤ f(x₂) (f(x₁) ≥ f(x₂)).

Неубывающие и невозрастающие функции объединяют общим названием монотонные функции.

Если для любых x₁ и x₂, принадлежащих Х, удовлетворяющих условию x₁ < x₂, справедливо неравенство f(x₁) < f(x₂) (f(x₁) > f(x₂)), то, как мы уже знаем, функция f(x) называется возрастающей (убывающей) на множестве Х. Возрастающие и убывающие функции называются также строго монотонными.

Следующая теорема устанавливает важный для решения практических задач признак возрастания и убывания функции и указывает правило для определения промежутков, на которых функция возрастает и убывает.

Теорема 6. Если функция f(x) имеет производную в каждой точке на интервале (a,b) и на f’(x) ≥ 0 (f’(x) ≤ 0) на (a,b), то функция f(x) не убывает (не возрастает) на (a,b).

Замечание. Теорема остается справедливой, если f’(x) > 0 (f’(x) < 0) на (a,b) , то f(x) возрастает (убывает) на (a,b).

Правило. Для определения промежутков возрастания и убывания следует решить неравенства f’(x) > 0 и f’(x) < 0.

При решении задач, в которых требуется определить промежутки возрастания и убывания функции, следует прежде всего определить область существования этой функции.

Пример. Определить промежутки, на которых функция f(x) = x³ – 12x + 11 возрастает и убывает.

Решение. Область определения функции – вся числовая прямая. Находим производную функции f’(x) = 3x² – 12. Из неравенства 3x² – 12 > 0 или x² > 4 , или √x² > 2, т.е. |x| > 2(либо x > 2, либо x < – 2), следует, что данная функция возрастает на интервалах (– ∞; – 2) и (2; + ∞), а из неравенства 3x² – 12 < 0 или x² < 4, или √x² < 2, т.е. |x| < 2 (– 2 < x < 2), следует, что данная функция убывает на интервале (– 2; 2).

ОТЫСКАНИЕ ТОЧЕК ЛОКАЛЬНОГО ЭКСТРЕМУМА ФУНКЦИИ

Определение. Точка называется точкой строгого локального макси­мума (минимума) функции , если для всех из некоторой - окрест­ности точки выполняется неравенство при (рис.58).

Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.

Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенство не обязано выполняться для всех значений в области определения функции, а должно выполняться лишь в некоторой окрестности точки . Очевидно, функция может иметь несколько локальных максимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то локального минимума.

Теорема 7 (необходимое условие локального экстремума).

Если функция имеет в точке локальный экстремум и дифференцируема в этой точке, то .

Теорема 2.9 имеет следующий геометрический смысл. Если , и - точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси (рис.59).

Теорема 8 (достаточное условие локального экстремума). Пусть функция 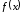дифференцируема в некоторой - окрестности точки . Тогда, если для всех из , а для всех из , то в точке функция имеет один и тот же знак, то в точке локального экстремума нет.

НАПРАВЛЕНИЕ ВЫПУКЛОСТИ И ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ

Пусть функция дифференцируема на интервале (а, b). Тогда существует касательная к графику функции в любой точке этого графика , причем касательная не параллельна оси Оу, поскольку ее угловой коэффициент, равный , конечен.

Определение. Будем говорить, что график функции имеет на (a, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (a, b).

Теорема 9. Если функция имеет не интервале (a, b) вторую производную и во всех точках (a, b), то график функции имеет на (а, b) выпуклость, направленную вниз (вверх).

Определение. Точка называется точкой перегиба графика функции , если в точке М график имеет касательную, и существует такая окрестность точки 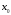, в пределах которой график функции слева и справа от точки имеет разные направления выпуклости.

Теорема 10(необходимое условие точки перегиба) Пусть график функции имеет перегиб в точке и пусть функция имеет в точке непрерывную вторую производную. Тогда в точке обращается в нуль, т.е.

Теорема 11(достаточное условие точки перегиба). Пусть функция 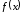имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах указной окрестности имеет разные знаки слева и справа от точки , то график имеет перегиб в точке .

СХЕМА ИССЛЕДОВАНИЯ ГРАФИКА ФУНКЦИИ

Изучение заданной функции и построение ее графика целесообразно проводить в следующем порядке:

Найти область определения функции;

Найти точки пересечения графика функции с осями координат;

Найти точки возможных экстремумов;

Найти критически точки

С помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремума и точки перегиба.

Построить график, учитывая исследование , проведенное в п.1)-5).

ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ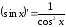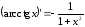