9.3 Управление процессами в условиях неопределенности

Неопределенность можно проклассифицировать по степени неопределенности (полная определенность, вероятностная, лингвистическая, интервальная, полная неопределенность), по характеру неопределенности (параметрическая, структурная, ситуационная) и по использованию получаемой в ходе управления информации (устранимая и неустранимая) [162].

Для широкого класса процессов априорная неопределенность может быть сведена к параметрической, когда вероятностные законы распределения для исследуемых ситуаций, величин и наблюдаемых процессов известны с точностью до конечного числа параметров.

Процессом можно управлять либо на основе априорных сведений в виде программы на весь период функционирования системы, либо с помощью процедур адаптивного и рекуррентного оценивания для устранения априорной параметрической неопределенности с использованием принципов управления с обратной связью. В этом случае принятие решения не сводится к единичному акту, а продолжается в ходе наблюдения за управляемым процессом.

В зависимости от степени изученности процесса может применяться структурная идентификация (когда неизвестна структура процесса и лежащие в его основе физические законы) или параметрическая идентификация (если неопределенность в представлении процесса можно свести к неопределенности векторного параметра).

В теории управления в условиях неопреважное место принадлежит задачам, в которых неизвестные параметры объекта управления заданы с точностью до априорных оценок, а процессы управления и идентификации должны происходить одновременно.

Последнее обстоятельство привело к появлению теории дуального управления [229], где, как правило, неизвестным параметрам приписываются вероятностные распределения, заданные с точностью до априорных оценок случайных величин.

Присутствие в процессе принятия решений неопределенности не позволяет точно оценить влияние управляющих воздействий на целевую функцию. Если неопределенности, существующие как в самой системе, так и в наблюдениях, могут быть представлены как стохастические процессы, то к таким задачам применимы методы стохастического управления. Однако имеется сравнительно большой класс проблем, при решении которых эти методы неэффективны. Последнее можно объяснить тем, что набор стандартных вероятностных понятий и методов оказывается неадекватным для описания рассматриваемых ситуаций [288], а также с трудностью получения необходимых статистических характеристик параметров, отсутствием эргодичности процессов и их существенной нестационарностью. Источник неопределенности может не иметь случайного характера, и иногда быть частично или полностью детерминированным. Сложность технологических комплексов и неопределенность информации о них растет, а требования к точности получаемого решения повышаются. Проблема представления неопределенности является одной из ключевых, но в то же время и наименее изученной для объектов газовой промышленности.

7.4 Интерполяция

Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Линейная и квадратичная интерполяцияявляются самыми простыми способами обработки таблиц и выполняются по уравнениям:

f(x)_лин = а₀+ а₁х. f(x)_кв = а₀+ а₁х + а₂х².

При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает простое соединение узловых точек отрезками прямых. В системе Mathcadдля этого используется функцияlinterp(X,Y,x), гдеXиY– вектора узловых точек. Функцияlinterp(X,Y,x) возвращает значение функции при её линейной интерполяции по заданным аргументам х. При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. Первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp не предназначена и за пределами области определения сигнала может вести себя непредсказуемо.

Полиномиальная интерполяция.Линейная и квадратичная аппроксимация являются частным случаем полиномиальной интерполяции с помощью аппроксимирующего полинома:

f(x) = а₀+ а₁х + а₂х²+ … + a_nxⁿ=a_i·xⁱ. (14.2.1)

Для выполнения полиномиальной интерполяции достаточно по выражению (14.2.1) составить систему линейных уравнений для n узловых точек и определить n значений коэффициентов a_i. Приглобальнойинтерполяции, по всем N точкам задания функции, степень полинома равна N-1.

Максимальная степень полинома на практике обычно устанавливается не более 8-10, а большие массивы данных интерполируются последовательными локальнымичастями.

Для практического использования более удобны формулы аппроксимации, не требующие предварительного определения коэффициентов аппроксимирующих полиномов. К числу таких формул относится интерполяционных многочлен по Лагранжу /40/. При аппроксимации функции у(х) многочленом n-й степени Y(x): Y(x) = ++……+. (14.2.2)

Кривые Безье.Для задач аппроксимации широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения. При использовании кривых Безье в компьютерной графике пользователь может задавать форму кривой интерактивно, двигая опорные точки курсором на экране.

Наглядный метод построения этих кривых был предложен де Кастелье в 1959 году. Метод основан на разбиении отрезков, соединяющих исходные точки в отношении t, а затем в рекурсивном повторении этого процесса для полученных отрезков:

(t) = (1-t)(t) +t(t), (14.2.3)

где нижний индекс - номер точки, верхний индекс - уровень разбиения. Уравнение кривой n-ого порядка задается уравнением: P(t) = (t).

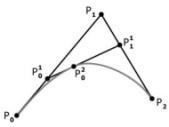
Рис. 14.2.3.

Для примера построим кривую для трех опорных точек P₀(t=0),P₁иP₂(t=1) на интервалеt=[0, 1] (рис. 14.2.3).

Для каждого t[0, 1] определим точку :

= (1-t)P₀ + tP₁,

= (1-t)P₁ + tP₂,

= (1-t) + t=(1-t)²P₀(t)+2t(1-t)P₁(t)+t²P₂(t),

и тем самым получим кривую второго порядка.

Рис. 14.2.3.

Аналогичным образом построение кривой Безье с четырьмя опорными точками будет определяться следующими выражениями:

= (1-t)P₀ + tP₁,

= (1-t)P₁ + tP₂,

= (1-t)P₂ + tP₃,

= (1-t) + t=(1-t)²P₀(t)+2t(1-t)P₁(t)+t²P₂(t),

= (1-t) + t=(1-t)²P₁(t)+2t(1-t)P₂(t)+t²P₃(t),

= (1-t) + t=(1-t)³P₀(t)+3t(1-t)²P₁(t)+ 3t²(1-t)P₂(t)+t³P₃(t).

Общая аналитическая запись для кривых Безье по N+1 опорной точке:

P^N(t) = P_i ,

= tⁱ (1-t)^N-i,

= N!/(i! (N-i)!) – биномиальные коэффициенты.

Кривые Безье всегда проходят через начальную P₀и конечную P_Nточки. Если рассматривать опорные точки в противоположном порядке, то форма кривой не изменяется. Если опорные точки лежат на одной прямой, то кривая Безье вырождается в отрезок, соединяющий эти точки. Степень многочлена, представляющего кривую в аналитическом виде, на 1 меньше числа опорных точек.

Сплайн -кусочный многочлен степениKс непрерывной производной степениK - 1в точках соединения сегментов.

При сплайновой интерполяции обычно используются локальные полиномы не выше третьей степени. Так, например, кубическиесплайны проходят через три смежные узловые точки (текущие опорные точки вычислений), при этом в граничных точках совпадают как значения полинома и функции, так и значения их первых и вторых производных. Коэффициенты полиномов, проходящих через три смежные узловые точки, рассчитываются так, чтобы непрерывными были первая и вторая его производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закреплённую в узловых точках. Это создает высокую плавность сплайнового полинома по сравнению с другими методами аппроксимации

Сплайновая аппроксимация может применяться для достаточно быстро изменяющихся функций, не имеющих разрывов функции и ее производных. Основной недостаток сплайнов – отсутствие единого аналитического выражения для описания функции. Попутно заметим также, что результаты экстраполяции функций, существенно зависят от метода аппроксимации, и, соответственно, к их достоверности нужно подходить достаточно осторожно.

спектральный метод интерполяции

При дискретизации данных с равномерным шагом по аргументу наиболее точную интерполяцию финитных сигналов обеспечивает спектральный метод. При условии, естественно, что в спектре сигнала не содержится частотных составляющих, превышающих частоту Найквиста.

Спектр дискретного сигнала.Допустим, что для обработки задается произвольный аналоговый сигнал s(t), имеющий фурье-образ S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шагt = 1/F =) с математических позиций означает умножение функции s(t) на гребневую (решетчатую) функцию Ш_(t) =(t-kt):

s_(t) = s(t) Ш_(t) = s(t)(t-kt) =s(kt)(t-kt). (14.4.1)

С учетом известного преобразования Фурье гребневой функции Ш_(t)FШ_F(f) фурье-образ дискретной функции s_(t):

S_F(f) = S(f) ③ FШ_F(f). (14.4.2)

Ш_F(f) =(f-nF). (14.4.3)

Отсюда, для спектра дискретного сигнала имеем:

S_F(f) = FS(f) ③(f-nF) = FS(f-nF). (14.4.4)

Спектр дискретного сигнала представляет собой непрерывную периодическую функциюс периодом F, совпадающую с функцией FS(f) непрерывного сигнала s(t) в пределах центрального периода от -f_Nдо f_N, где f_N = 1/2t = F/2 - частота Найквиста. Частота дискретизации сигнала должна быть минимум в два раза выше максимальной частотной составляющей в спектре сигнала (F = 1/t2f_max). Умножая функцию (14.4.2) на прямоугольную весовую функцию П_F(f), равную 1 в пределах главного частотного, получаем непрерывный спектр в бесконечных по частоте границах, равный спектру FS(f) в пределах главного частотного диапазона:

FS(f) = F[S(f) ③ Ш_F(f)] П_F(f). (14.4.5)

Обратное преобразование Фурье этого спектра, с учетом коэффициента F, должно восстанавливать непрерывный сигнал, равный исходному аналоговому сигналу s(t).

Интерполяционный ряд Котельникова-Шеннона. Произведем обратное преобразование обеих частей равенства (14.4.5). Умножение непрерывного и бесконечного спектра на П-импульс в пределах главного диапазона отобразится в динамической области сверткой двух функций:

Fs(t) = Fs_(t) ③ sinc(Ft).

s(t) = sinc(Ft) ③s(kt)(t-kt),

Отсюда, с учетом равенства (t-kt) ③ sinc(Ft) = sinc[F(t-kt)], получаем:

s(t) =s(kt) sinc[F(t-kt)]. (14.4.6)

Эта формула носит название интерполяционного ряда Котельникова-Шеннона и, по существу, является разложением сигнала по системе ортогональных функций sinc(F(t-kt)) = sinc((t/t – k)). С другой стороны, эта формула представляет собой свертку дискретной функции данных s(kt) с непрерывной функцией интегрального синуса. Для больших массивов дискретных данных точность восстановления сигнала обычно ограничивается интервалом задания функции интегрального синуса, по которому устанавливается интервал суммирования.

Из совокупности выше приведенных формул следует, что если для частоты дискретизации сигнала справедливо неравенство F 2f_max, где f_max - наибольшая частота в спектре произвольной непрерывной функции s(t), то функция s(t) может представляться в виде числовой последовательности дискретных значений s(kt), k = 0,1,2,..., и однозначно по этой последовательности восстанавливаться, в пределе - без потери точности. В этом и состоит сущность теоремы отсчетов Котельникова-Шеннона.