40. Динамика бокового движения. Уравнения движения.

Боковое движение составляют вращения вокруг осе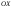й и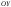и перемещение в направлении оси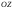. Уравнения движения ЛА линеаризуют, пользуясь разделением движения по отдельным каналам. Реализация бокового движения при малых отклонениях возможна при следующих условиях:– исходное невозмущенное движение является продольным;– можно пренебречь аэродинамическими и гироскопическими связями между продольным и боковым движениями ввиду малости связей. Нелинейные дифференциальные уравнения бокового движения имеют вид: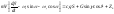

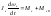
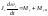
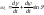
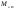
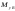
где 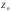– возмущающие моменты и сила,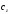– коэффициент боковой силы. Для полного описания движения центра масс ЛА необходимо взять кинематическое уравнени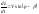егде– координата бокового отклонения от заданной траектории полета.Проведем линеаризацию уравнений, предполагая, что установившиеся значения величин равны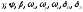нулю. После преобразования линейная математическая модель бокового движения ЛА, устанавливающая связь между регулируемыми величинами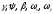и регулирующими факторами, имеет вид: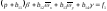;;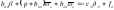;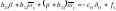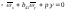, где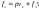,,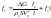,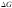– изменение веса (сброшенный груз и т.д.),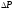– разность тяг двигателей,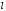– характерная длина, например, размах крыльев,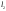– плечо момента крена,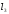– расстояние между двигателями, имеющими разные тяги,– возмущения, вызванные, например, ударными волнами, образованными пролетающими вблизи ЛА, взрывами и т.д. К этим уравнениям следует добавить кинематические уравнения: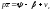;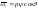, где,,,.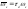

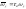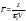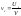41. Частные случаи бокового движения. Передаточные функции.

1. Движение рыскания без крена. При таком движении продольная ось ЛА совершает колебания относительно вектора скорости, поворот которого не учитывается. Примем , получим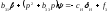В этом уравнении уголесть угол между вектором скорости и продольной осью ЛА. Следовательно, этот угол равен углу скольжения, т.е.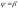и уравнение принимает вид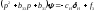Передаточная функция будет

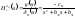2. Плоское движение со скольжением при неизменном угле крена. Полагая в уравнениях 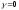, получим (при выводе этих уравнений предположено, что угол атакиблизок к нулю, поэтому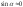и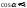)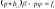,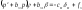Из уравнений получает выражения для ПФ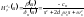,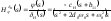где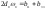,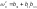.3.Движение в начальный момент крена ЛА. Пренебрегая изменением курса и опустив третье уравнение в системе, получим

;.

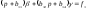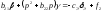Отсюда находим выражения для передаточных функций, полагая :

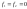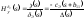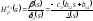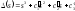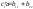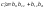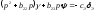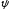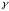,где;;;.4.Движение по крену без скольжения. В этом случае из системы при пренебрежении моментом рыскания находим: Отсюда, решая относительнои, получим: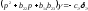;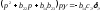. а передаточные функции будут иметь вид:,.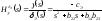

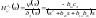42. Характеристики возмущенной атмосферы.

Ветровое возмущение. Существуют различные виды воздушных потоков: постоянные ветры, восходящие и нисходящие потоки, порывы ветра, завихрения и т.д.Действие порывов ветра вызывает отклонение ЛА от заданной траектории полета, увеличивает перегрузки, действующие на ЛА, и ухудшает управляемость.Порывы ветра большой интенсивности могут быть приняты в пределе как скачки скорости ветра. Движущимся ЛА такой скачок воспринимается как импульс. В ряде случаев более важными являются не единичные порывы ветра, а случайные возмущения, состоящие из нерегулярно чередующихся единичных порывов ветра. Такие нерегулярные порывы ветра называются турбулентностью атмосферы. В простейшем случае модель турбулентной атмосферы рассматривается как стационарный случайный процесс и задается соответствующей корреляционной функцией 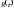или спектральной плотностью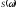. Имея реализацию случайного процесса, можно найти корреляционную функцию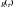и спектральную плотность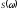порывов ветра: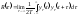,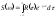Определим реакцию ЛА на турбулентные возмущения. Предположим, например, что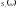– спектральная плотность вертикальных порывов ветра, соответствующая скорости порывов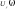, и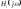– частотная характеристика ЛА в продольном движении, отражающая реакцию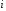-й координаты ЛА на ветровые порывы. Тогда спектральная плотность интенсивности реакции ЛА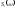на вертикальные порывы будет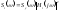а дисперсияреакции ЛА на порывы ветра: