Тема 3 характеристики векторного поля

3.1 Дивергенція (розбіжність) векторного поля

Нехай дано векторне поле . Виберемо довільну точку в просторі та обведемо її деякою гладкою (або кусково-гладкою) замкненою поверхнею . Тоді потік векторного поля через цю поверхню у напрямі зовнішньої нормалі дорівнює

.

Позначимо через об’єм тіла, обмеженого поверхнею . Тоді 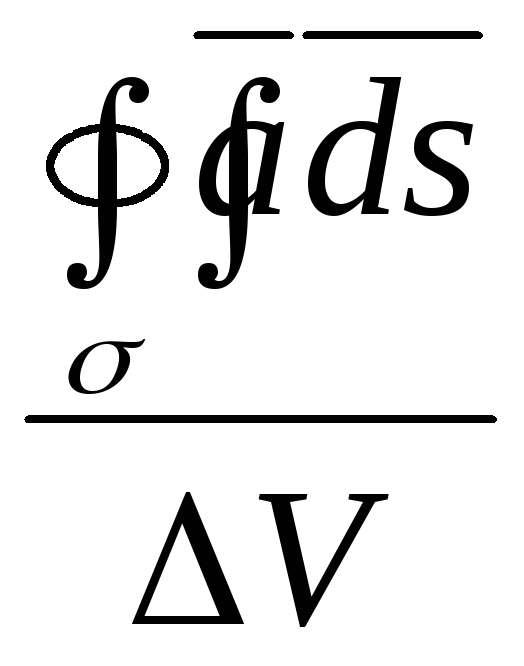характеризує питому продуктивність джерел, що містяться усередині поверхні (питома потужність джерел).

Будемо стягувати поверхню в точку . Границя, до якої при цьому прямує середня потужність джерел, називається дивергенцією векторного поля в точці і позначається символом , тобто

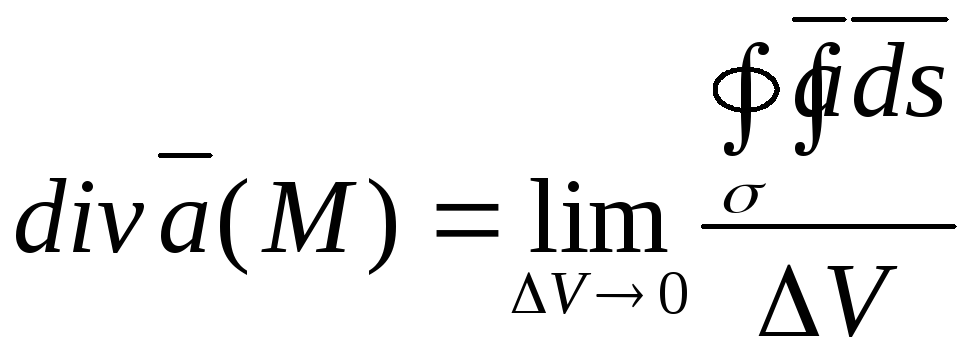. (3.1)

Обчислення дивергенції за означенням пов’язане з необхідністю граничного переходу, що ускладнює викладки. Однак слід відмітити, що за допомогою цієї формули ми можемо визначити джерела та стоки: ті точки, в яких дивергенція додатна, називаються джерелами, а ті, в яких вона від’ємна, називаються стоками.

3.2 Обчислення дивергенції векторного поля в декартовій системі координат

Розглянемо векторне поле :

,

де – проекції вектора на координатні осі, неперервні функції.

Знайдемо , де .

Візьмемо прямокутний паралелепіпед з центром у точці із ребрами , , (рис. 3.1).

Рисунок 3.1

Потік вектора через зовнішню поверхню цього паралелепіпеда дорівнює:

П=П₁+П₂+П₃+П₄+ П₅+П₆, (3.2)

де П₁ – потік векторного поля через зовнішню сторону грані ,

П₂ – потік векторного через зовнішню сторону грані ,

П₃ – потік векторного поля через зовнішню сторону грані ,

П₄ – потік векторного поля через зовнішню сторону грані ,

П₅ – потік векторного поля через зовнішню сторону грані ,

П₆ – потік векторного поля через зовнішню сторону грані .

Обчислимо П₁ – потік векторного поля через зовнішню сторону грані . Вектор нормалі до цієї поверхні паралельний осі і співнапрямлений з одиничним вектором , причому .

Будемо вважати, що векторне поле постійне і таке, як у точці , тоді проекція вектора на напрям нормалі буде:

.

Отже, потік векторного поля через зовнішню сторону грані дорівнює:

П₁= (3.3)

Обчислимо П₂ – потік векторного поля через зовнішню сторону грані . Вектор нормалі до цієї поверхні паралельний осі , але має напрям протилежний напяму одиничного вектора , тобто .

Будемо вважати, що векторне поле постійне і таке, як у точці , тоді потік векторного поля через зовнішню сторону грані буде:

П₂= (3.4)

Обчислимо П₃ – потік векторного поля через зовнішню сторону грані . Вектор нормалі до цієї поверхні паралельний осі і співнапрямлений з одиничним вектором . Будемо вважати, що векторне поле постійне і таке, як у точці , тоді потік векторного поля по зовнішній стороні грані буде:

П₃= (3.5)

Аналогічно, П₄ – потік векторного поля через зовнішню сторону грані обчислюється за формулою:

П₄=, (3.6)

де одиничний вектор нормалі до цієї поверхні .

Потік через зовнішню сторону грані із одиничним вектором нормалі обчислюється за формулою:

П₅=, (3.7)

а потік П₆ через зовнішню сторону грані із одиничним вектором нормалі дорівнює:

П₆=. (3.8)

Тоді, враховуючи рівності (3.2)–(3.8), маємо:

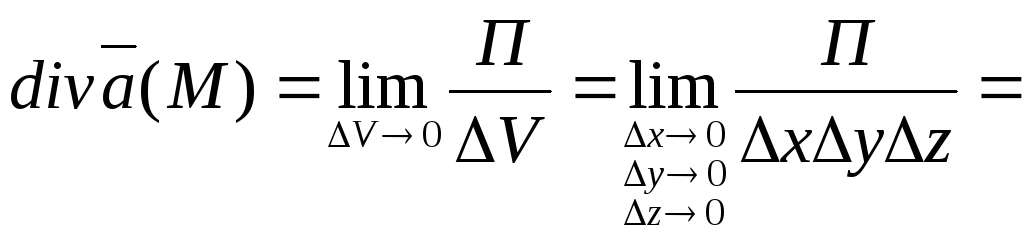
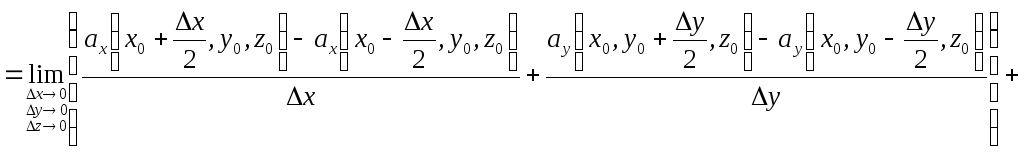
Отже,

(3.9)

Приклад 3.1 Визначити, в яких точках векторне поле має джерела, а в яких – стоки, якщо , , .