
- •Тема 1 скалярне поле та його характеристики 5
- •Тема 2 поняття векторного поля та його потоку 16
- •Тема 3 характеристики векторного поля 41
- •Тема 4 сПеЦіальні типи полів 79
- •Передмова
- •Тема 1 скалярне поле та його характеристики
- •1.1 Похідна за напрямом
- •Розв’язування
- •1.2 Поняття та властивості градієнта
- •Доведення
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 поняття векторного поля та його потоку
- •2.1 Потік векторного поля
- •2.2 Обчислення потоку векторного поля
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.3 Формула Остроградського-Гаусса
- •Розв’язування
- •Р озв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 характеристики векторного поля
- •3.1 Дивергенція (розбіжність) векторного поля
- •3.2 Обчислення дивергенції векторного поля в декартовій системі координат
- •Розв’язування
- •Розв’язування
- •3.3 Проекція ротора векторного поля на вектор нормалі та ротор векторного поля
- •Розв’язування
- •Розв’язування
- •3.4. Оператор Гамільтона
- •Розв’язування
- •3.5 Диференціальні операції другого порядку
- •Розв’язування
- •3.6 Властивості ротора векторного поля
- •Розв’язування
- •3.7 Циркуляція векторного поля та її обчислення. Формула Стокса
- •Розв’язування
- •Розв’язування
- •Р озв’язування
- •Розв’язування
- •3.8 Основні операції векторного аналізу в криволінійних координатах
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 сПеЦіальні типи полів
- •4.1 Потенціальні векторні поля
- •Розв’язування
- •4.2 Соленоїдні (трубчасті) поля
- •Розв’язування
- •4.3 Гармонічне поле
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Література
- •Наталія Василівна Сачанюк-Кавецька Лідія Іванівна Педорченко Елементи теорії поля
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
Розв’язування
Потік через повну поверхню циліндра дорівнює
П=![]()
де
![]() – нижня основа циліндра,
– нижня основа циліндра,
![]() – бічна поверхня
циліндра,
– бічна поверхня
циліндра,
![]() – верхня основа
циліндра.
– верхня основа
циліндра.
Для обчислення
![]() діятимемо так. Виберемо на бічній
поверхні циліндра довільну точку
діятимемо так. Виберемо на бічній
поверхні циліндра довільну точку
![]() ,
побудуємо вектор поля в цій точці і
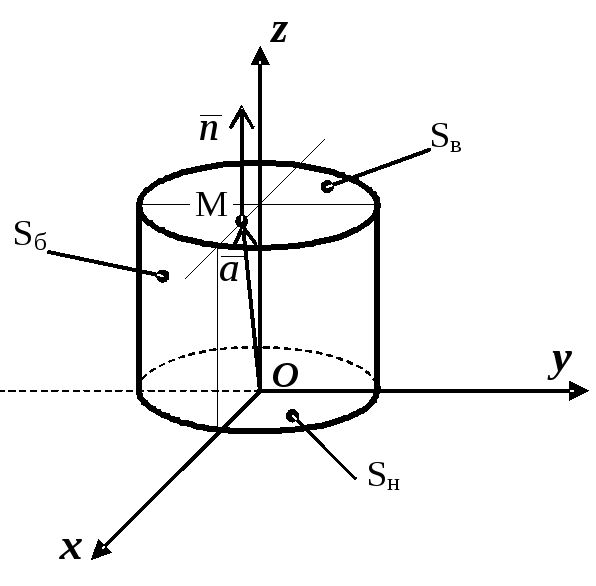
проведемо нормаль до поверхні. З рис.
2.3 бачимо, що
,
побудуємо вектор поля в цій точці і
проведемо нормаль до поверхні. З рис.
2.3 бачимо, що
![]() дорівнює радіусу циліндра, тобто
дорівнює радіусу циліндра, тобто
![]() .
Тоді
.
Тоді
![]() .
.
Тобто,
![]() дорівнює площі бічної поверхні циліндра.
дорівнює площі бічної поверхні циліндра.
 Для
обчислення інтеграла
Для
обчислення інтеграла
![]() чинимо аналогічно попередньому випадку
(рис. 2.4).
чинимо аналогічно попередньому випадку
(рис. 2.4).
Рисунок 2.4
З рис. 2.4 бачимо,
що
![]() є сталою і дорівнює висоті циліндра,
тобто
є сталою і дорівнює висоті циліндра,
тобто
![]() .
Отже,
.
Отже,
![]() ,
,
оскільки радіус
циліндра дорівнює одиниці. Тобто, потік
вектора
![]() через верхню основу циліндра дорівнює
подвоєній площі цієї основи.
через верхню основу циліндра дорівнює
подвоєній площі цієї основи.

 Обчислимо
Обчислимо
![]() .
На даній поверхні
виберемо довільну точку
.
На даній поверхні
виберемо довільну точку
![]() і зобразимо вектор поля в цій точці та
вектор нормалі до поверхні (рис. 2.5).
і зобразимо вектор поля в цій точці та
вектор нормалі до поверхні (рис. 2.5).
Рисунок 2.5
З рис. 2.5 видно, що
вектор поля перпендикулярний вектору
нормалі і
![]() в довільній точці поверхні
в довільній точці поверхні
![]() .Отже:
.Отже:
![]() .
.
Таким чином, потік векторного поля через поверхню циліндра дорівнює:
П![]() .
.
Приклад 2.3
Обчислити
потік вектора
![]() через поверхню
через поверхню
![]()
Розв’язування
В даному випадку
![]() не є постійною на усій поверхні, тому
для обчислення потоку застосуємо формулу
(2.14). Оскільки
не є постійною на усій поверхні, тому
для обчислення потоку застосуємо формулу
(2.14). Оскільки
![]() ,
то формула (2.14) набуває вигляду:
,
то формула (2.14) набуває вигляду:
П=![]()
де
![]() – проекція поверхні
– проекція поверхні
![]() на координатну площину
на координатну площину
![]() .
.
Побудуємо задану
поверхню та її проекцію на площину
![]() (рис. 2.6).
(рис. 2.6).
Р
О исунок
2.6
исунок
2.6
Визначимо нормальний
вектор до поверхні
![]() :
:
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
За формулою (2.15)
.
За формулою (2.15)
![]() .
Оскільки за формулами (2.16)
.
Оскільки за формулами (2.16)
![]() для всіх
для всіх
![]() ,
то при обчисленні
потоку перед подвійним інтегралом
ставимо знак «плюс».
,
то при обчисленні
потоку перед подвійним інтегралом
ставимо знак «плюс».
Тоді,
П=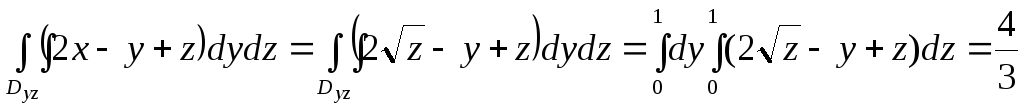 .
.
2.3 Формула Остроградського-Гаусса
Формула Остроградського-Гаусса встановлює зв’язок між поверхневим інтегралом по замкненій поверхні і потрійним інтегралом по просторовій області, обмеженій цією поверхнею.
Розглянемо деяке
векторне поле
![]() .
Нехай в просторі задано правильну
область
.
Нехай в просторі задано правильну
область
![]() ,
обмежену замкненою поверхнею
,
обмежену замкненою поверхнею
![]() ,
проекцією якої на координатну площину
,
проекцією якої на координатну площину
![]() є правильна область
є правильна область
![]() (рис. 2.7). Поверхня
(рис. 2.7). Поверхня
![]() може бути розбита на нижню поверхню
може бути розбита на нижню поверхню
![]() ,
яка задається рівнянням
,
яка задається рівнянням
![]() ,
верхню поверхню
,
верхню поверхню
![]() ,
яка задається рівнянням
,
яка задається рівнянням
![]() ,
та бічну циліндричну поверхню
,
та бічну циліндричну поверхню
![]() з твірною, паралельною осі
з твірною, паралельною осі
![]() .
.
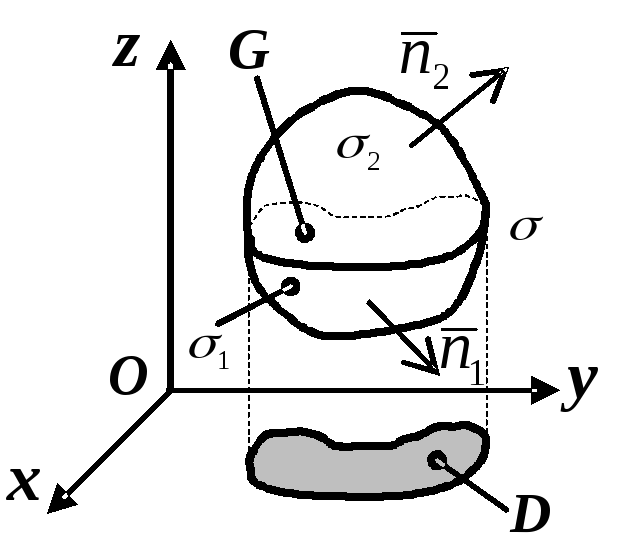
Рисунок 2.7
Тоді потрійний
інтеграл по області
![]() функції
функції
![]() дорівнює поверхневому інтегралу
векторного поля
дорівнює поверхневому інтегралу
векторного поля
![]() по поверхні
по поверхні
![]() .
Тобто,
.
Тобто,
![]() ,(2.17)
,(2.17)
або
![]() (2.18)
(2.18)
Формули (2.17), (2.18) називають формулою Остроградського-Гаусса. Доведемо цю формулу.
Розглянемо інтеграл
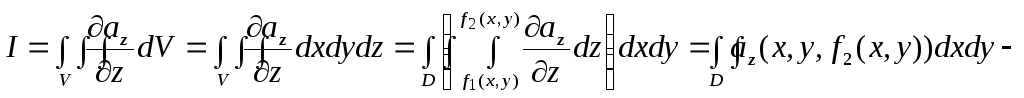
![]() .
(2.19)
.
(2.19)
Оберемо напрям
нормалі до поверхні, який збігається
із напрямом зовнішньої нормалі. Тоді
![]() на поверхні
на поверхні
![]() –
додатний, на поверхні
–
додатний, на поверхні
![]() – від’ємний, а на поверхні
– від’ємний, а на поверхні
![]() – рівний нулю. Тому:
– рівний нулю. Тому:
![]() , (2.20)
, (2.20)
![]() , (2.21)
, (2.21)
![]() . (2.22)
. (2.22)
З формул (2.20) – (2.22) випливає, що
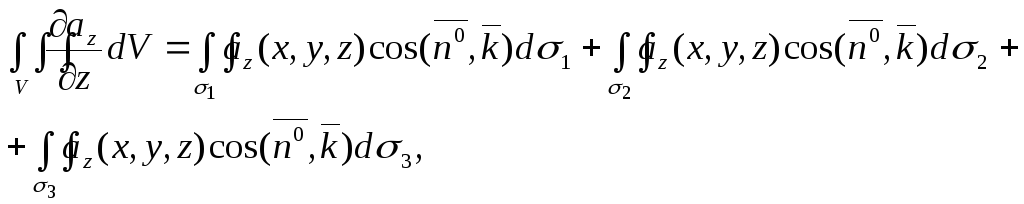
або
![]() . (2.23)
. (2.23)
Аналогічно можна одержати, що
![]() , (2.24)
, (2.24)
![]() . (2.25)
. (2.25)
Додавши рівності (2.23)–(2.25), отримуємо формулу Остроградського:
![]() .
.
Приклад 2.4
Знайти потік векторного поля
![]()
-
через верхню сторону трикутника
 ,
утвореного при перерізі площини
,
утвореного при перерізі площини
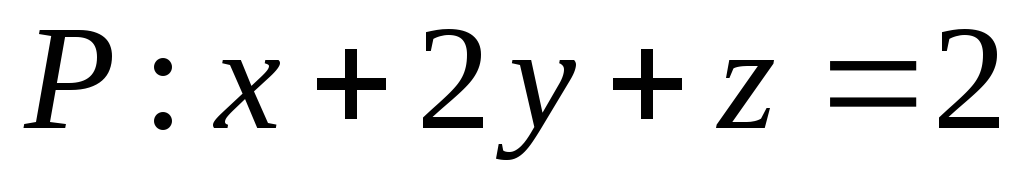 з координатними площинами;
з координатними площинами; -
через повну поверхню піраміди, утвореної площиною
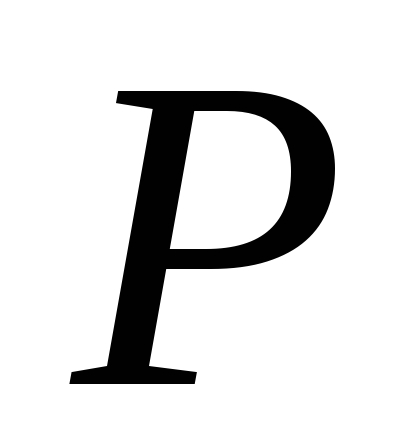 і координатними площинами:
і координатними площинами:
а) безпосередньо;
б) за формулою Остроградського-Гаусса.
