1.1 Похідна за напрямом

Нехай задано скалярне поле . Візьмемо в ньому точку і проведемо з цієї точки вектор , напрямні косинуси якого , (рис. 1.1).

На векторі на відстані від його початку візьмемо точку .

Тоді .

Рисунок 1.1

Обчислимо тепер приріст функції при переході від точки до точки в напрямі вектора :

Якщо існує границя відношення при , то цю границю називають похідною функції в точці за напрямом вектора і позначають , тобто

. (1.4)

Виведемо формулу для обчислення похідної за напрямом. Припустимо, що функція диференційовна в точці . Тоді її повний приріст в цій точці можна записати так:

(1.5)

де – нескінченно малі функції при .

Оскільки

, (1.6)

то вираз (1.5) набуває вигляду

(1.7)

Перейшовши в рівності (1.7) до границі при , дістанемо формулу для обчислення похідної за напрямом

(1.8)

З формули (1.8) випливає, що частинні похідні є окремими випадками похідної за напрямом. Дійсно, якщо збігається з одним із ортів , то похідна за напрямом збігається з відповідною частинною похідною. Наприклад, якщо , то , тому

Подібно до того, як частинні похідні характеризують швидкість зміни функції в напрямі осей координат, так і похідна показує швидкість зміни скалярного поля в точці за напрямом вектора .

Абсолютна величина похідної відповідає значенню швидкості, а знак похідної визначає характер зміни функції в напрямі (зростання чи спадання).

Очевидно, що похідна за напрямом, протилежним напряму , дорівнює похідній за цим напрямом, взятій з протилежним знаком.

Справді, при зміні напряму на протилежний кути збільшуються на величину , тому

Фізичний зміст цього результату такий: зміна напряму на протилежний не впливає на значення швидкості зміни поля, а тільки на характер цієї зміни.

Приклад 1.1 Знайти похідну скалярного поля в точці в напрямі точки .

Розв’язування

Похідну скалярного поля в точці обчислимо за формулою (1.8).

Для цього знайдемо частинні похідні скалярного поля за кожною змінною та обчислимо значення цих похідних в точці :

,

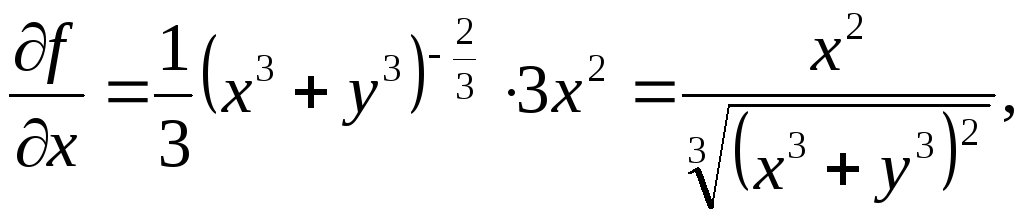
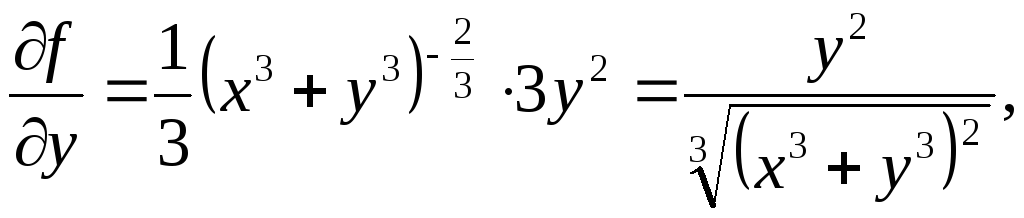
Обчислимо напрямні косинуси вектора . Оскільки , то

Отже,

тобто .

1.2 Поняття та властивості градієнта

Нехай задано поле і точку. У якому напрямі похідна має найбільше значення? Відповідь на це запитання має важливе практичне значення і дається на основі поняття градієнта поля.

Вектор, координати якого є значення частинних похідних функції в точці , називають градієнтом функції в цій точці і позначають . Отже,

. (1.9)

Зв’язок між градієнтом та похідною в даній точці за довільним напрямом показує така теорема.

Теорема. Похідна функції в точці за напрямом вектора дорівнює проекції градієнта функції в цій точці на вектор , тобто

. (1.10)

Доведення

Нехай – кут між градієнтом (1.9) і одиничним вектором (рис. 1.2). Тоді з властивостей скалярного добутку дістанемо

. Тобто, . Що і треба було довести.

Рисунок 1.2

Зазначимо деякі властивості градієнта.

1. Похідна в даній точці за напрямом вектора має найбільше значення, якщо напрям цього вектора збігається з напрямом градієнта, причому

. (1.11)

Справді, з формули (1.10) випливає, що похідна за напрямом досягає максимального значення (1.11), якщо , тобто, якщо напрям вектора збігається з напрямом градієнта.

Таким чином, швидкість зростання скалярного поля в довільній точці є максимальною у напрямі градієнта. Зрозуміло, що у напрямі, протилежному напряму градієнта, поле найшвидше зменшуватиметься.

2. Похідна за напрямом вектора, перпендикулярного до градієнта, дорівнює нулю. Іншими словами, скалярне поле залишається сталим у напрямі, перпендикулярному до градієнта.

Дійсно, за формулою (1.10) , якщо .

3. Вектор-градієнт у кожній точці поля перпендикулярний до поверхні рівня, яка проходить через цю точку.

Це твердження випливає з того, що напрямний вектор нормалі до поверхні рівня, яка проходить через точку , має координати

4. Справедливі рівності:

;

Доведемо, наприклад, третю рівність. Маємо:

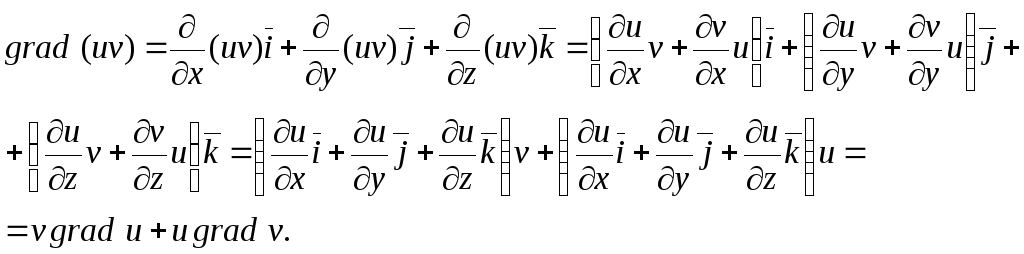
Решта рівностей доводяться аналогічно.

Приклад 1.2 Знайти величину і напрям градієнта скалярного поля в точці .