Розв’язування

Умовою соленоїдності векторного поля є рівність: . Знайдемо координати вектора . Маємо

, де

. Обчислимо дивергенцію векторного поля :

.

Отже, векторне поле є соленоїдним.

4.3 Гармонічне поле

Векторне поле , яке є одночасно потенціальним (безвихровим) і соленоїдним (трубчастим), називається гармонічним. Оскільки поле потенціальне, то його можна записати у вигляді:

,

де – потенціал поля.

Умова соленоїдності означає, що

.

Таким чином, , але

.

Функція , яка задовольняє умову

, (4.5)

називається гармонічною.

Приклад 4.3 Перевірити, чи дане векторне поле є

а) потенціальним,

б) соленоїдним.

У випадку потенціальності поля знайти його потенціал.

Розв’язування

Знайдемо :

.

Отже, векторне поле є потенціальним. Знайдемо :

.

Отже, векторне поле є соленоїдним. Знайдемо потенціал векторного поля:

,

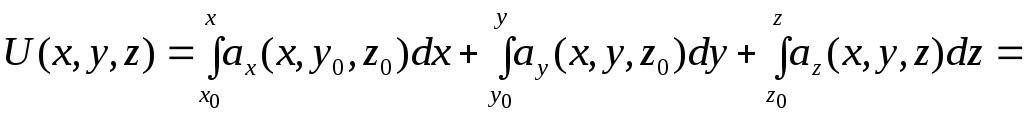
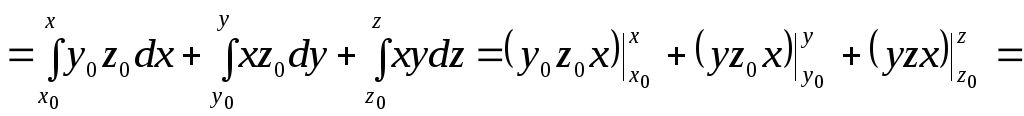
де .

Питання для самоперевірки

1. Яке векторне поле називається потенціальним?

2. Що називають потенціалом поля?

3. Поясніть відмінність термінів «потенціал» та «потенціальна функція».

4. Вкажіть властивості потенціальних полів.

5. Наведіть приклади потенціальних полів.

6. Виведіть формулу знаходження потенціалу поля.

7. Яке поле називають соленоїдним?

8. Що таке векторний потенціал поля?

9. Вкажіть властивості соленоїдних полів.

10. Що таке диполь?

11. Проаналізуйте центрально-симетричне поле ,

де , , .

12. Яке поле називається гармонічним?

13. Запишіть умову гармонічності поля.

14. Перевірити, чи векторне поле , де , , , є соленоїдним.

15. Перевірити, чи векторне поле є гармонічним, знайти його потенціал.

Завдання для самостійної роботи

Завдання 4.1

Перевірити, чи є векторне поле потенціальним і соленоїдним. У випадку потенціальності поля обчислити його потенціал:

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

24. .

25. .

26. .

27. .

28. .

29. .

30. .

31. .

32. .

33. .

34. .

35. .

36. .

37. .

38. .

39. .

40. .

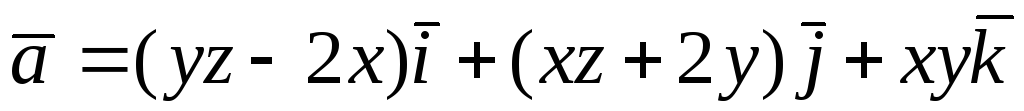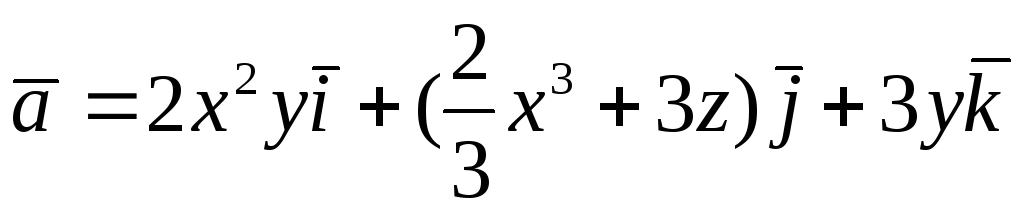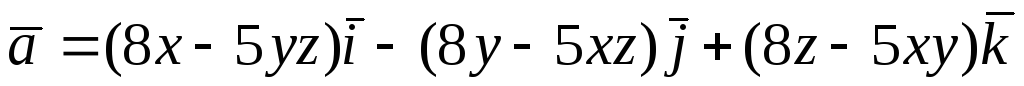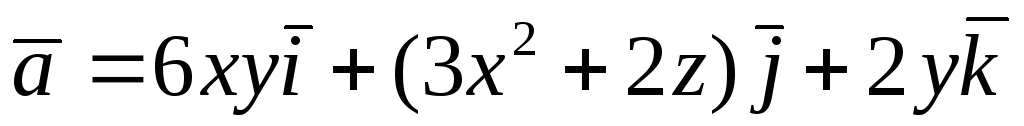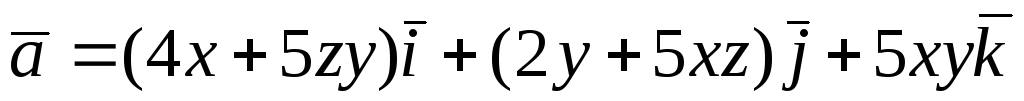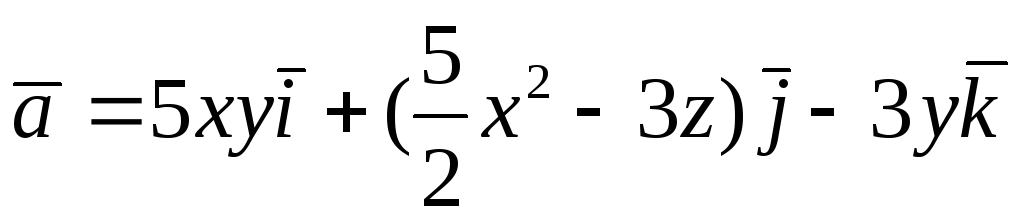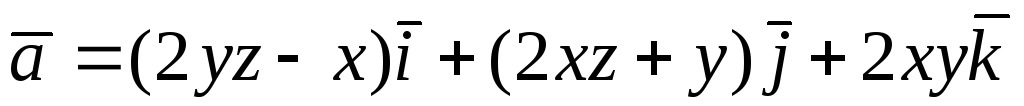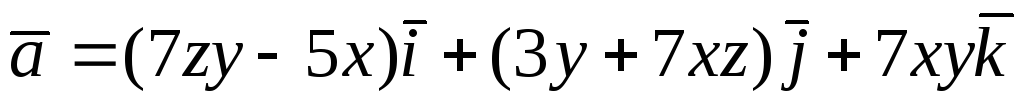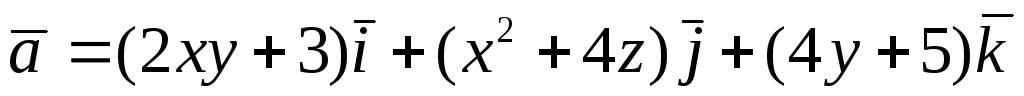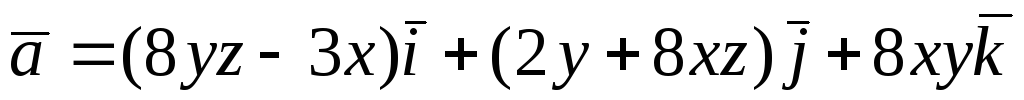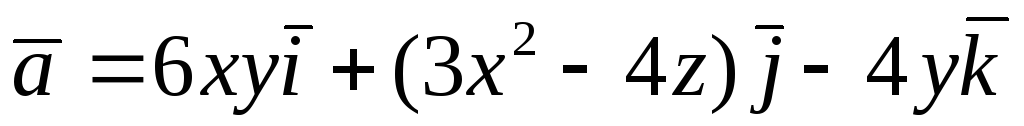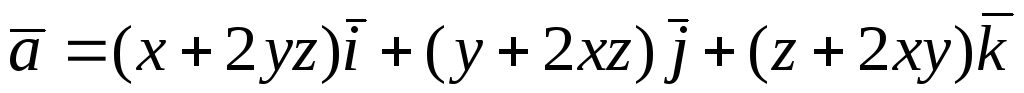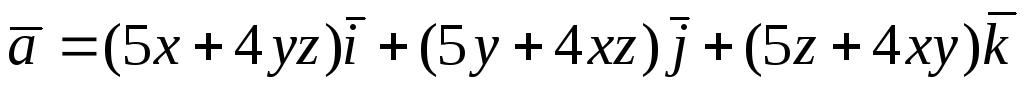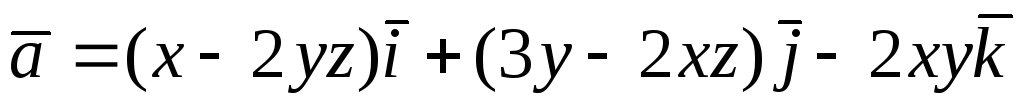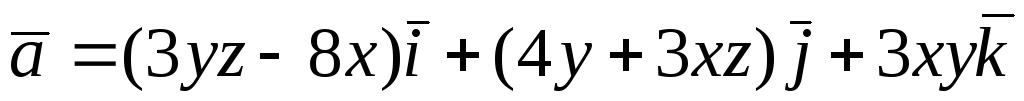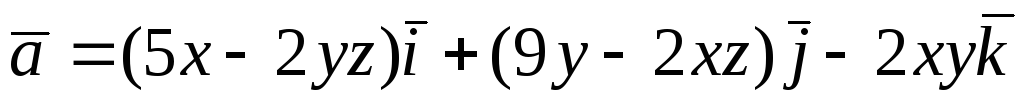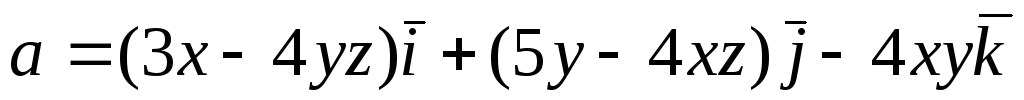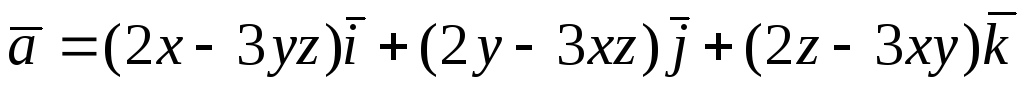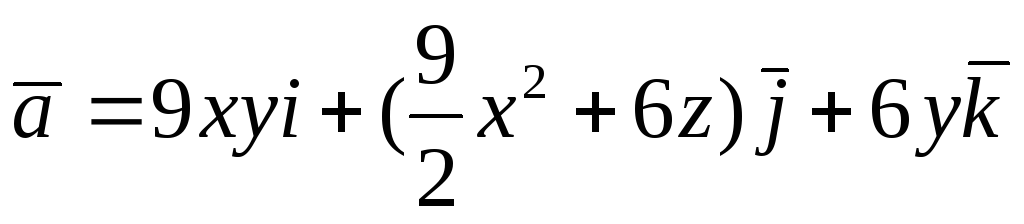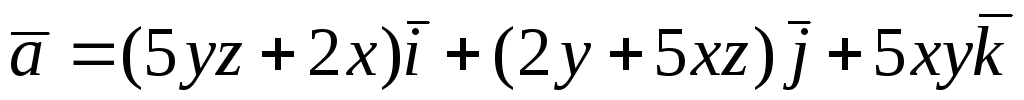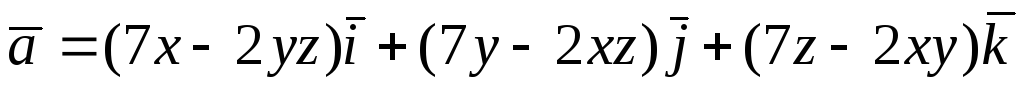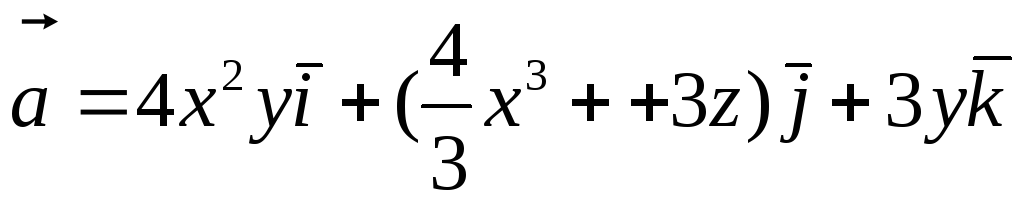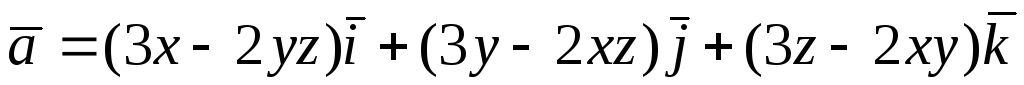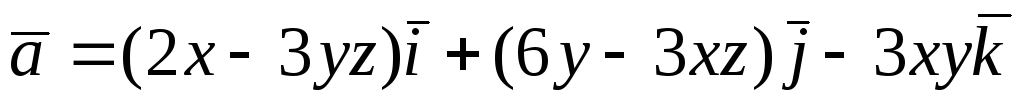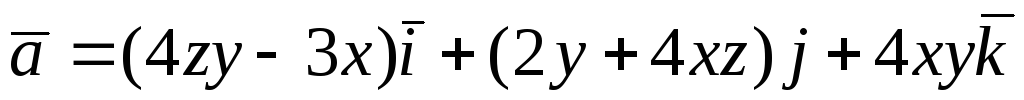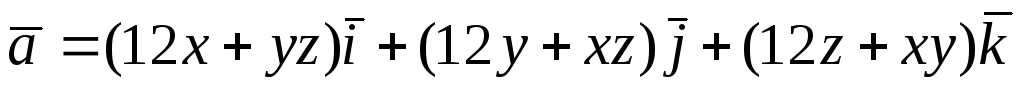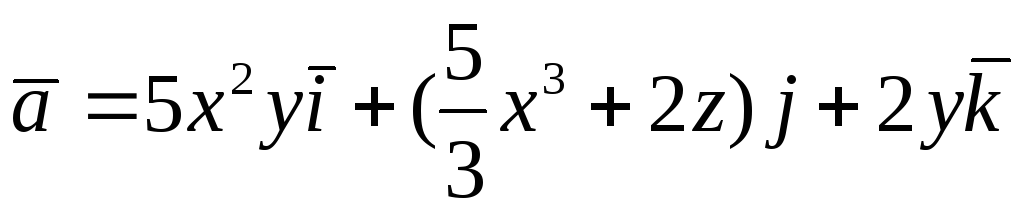Література

1. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний, 2-е изд. – М.: Физматгиз, 1959. – 325 с.

2. Васильченко І.П., Данилов В.Я., Лобанов А.І., Тарах Є.Ю. Вища математика: Основні означення, приклади і задачі /Навч. посібник. Кн. 2 – друге вид., зі змінами. – К.:Либідь, 1994. – 280 с.

3. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч.Ч. ІІ. – М.: Высшая школа, 1986. – 415 с.

4. Демидович Б.П., Марон И.А. Основы вычислительной математики, 3-е изд. – М.: Наука, 1966. – 455 с.

5. Дюженкова Л.І., Дюженкова О.Ю., Михайлін Г.О. Вища математика: Приклади і задачі. Посібник. – К.: Видавничий центр «Академія», 2002. – 624 с.

6. Сборник задач по математике для втузов. Ч.2. Специальные разделы математического анализа /Под ред. А.В. Ефимова, Б.П. Демидовича. – 2-е изд. – М.: Наука, 1986. – 368 с.

7. Мышкис А.Д. Математика для технических вузов: Специальные курсы. 2-е изд. – СПб.: Издательство «Лань», 2002. – 640 с. – (Учебники для вузов. Специальная литература).

8. Чинаев П.И., Черенков А.А., Минин Н.А., Перевозников А.Ю. Высшая математика. Специальные главы. – К.: Вища школа, 1977. – 368 с.

9. Шкіль М.І., Колесник Т.В. Вища математика. – К.: Вища школа, 1986. – 521 с.

10. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. – М.: Наука, 1965. – 424 с.

Навчальне видання